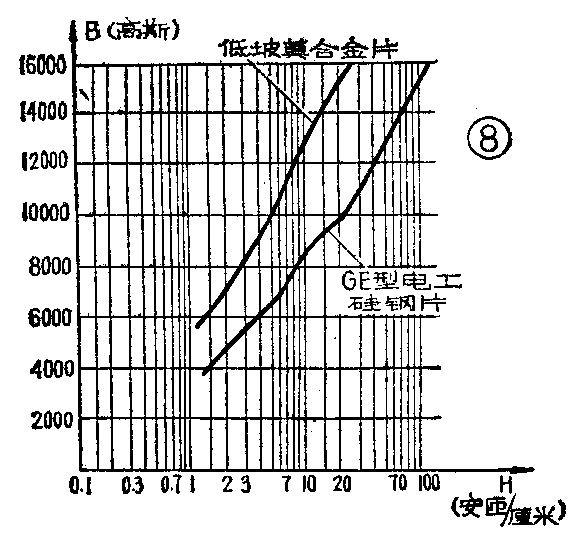
图⑧是常用的两种铁磁材料的磁化曲线,为了绘制方便,磁场强度H是按对数排列。
设计举例
例如设计供给6F3、6P15、6P1、6N1、6A2、6N2,六只电子管的灯丝电源。要求电源电压在180~240伏之间供电时,灯丝电压稳定在±10%以内。
由电子管手册中查到:上述各电子管的灯丝电流依次分别为0.9、0.8.0.65、0.6、0.3、0.3安。
按照尽量减少电流差别的原则,确定采用串并联混合形式。故六只电子管接成如图⑨形式。
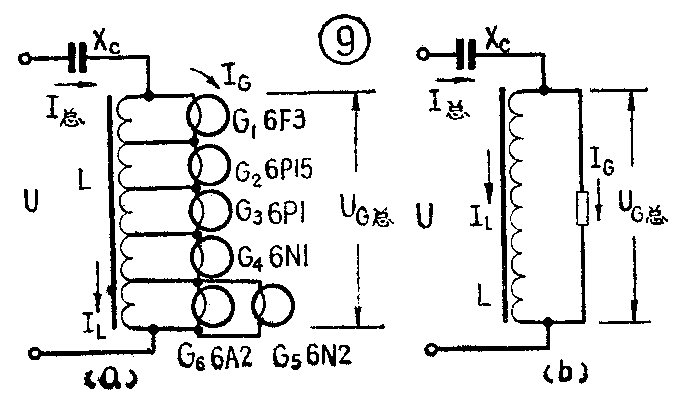
图⑨中灯丝电流各不相等,由于采用电感抽头的方法,使电感各抽头之间的磁化电流也不相等,总磁场强度等于各组的安匝数之和。为计算简便,可将图⑨a画出图⑨b的等效电路图。取各灯丝电流I\(_{G}\)的平均值,故电感L的磁场强度等于流经电感L的平均电流IC与匝数的乘积。总电流I\(_{总}\),由电感支路的电流IL和灯丝支路电流I\(_{G}\)两个电流分量组成。U、I总、I\(_{G}\)和IL的值均为变量。主要需求出,在电源电压U变化下,流经电感L的变化电流L及确定串联电容的容量C的值。
求解的顺序为:灯丝总端电压和灯丝平均变化电流——应补偿的灯丝电流→确定最小磁化电流→最小总电流→最大总电流→最大磁化电流→求出谋戎怠范üぷ鞫巍蟪龃呕苍选慕孛婊枷咧本丁缛荨
下面按照这一顺序进行计算。
(1)求解灯丝总端电压U\(_{G}\)和平均灯丝电流IG及平均灯丝电流变动范围G。
U\(_{G}\)=UG1+U\(_{G2}\)+……UGn即总端电压U\(_{G}\)为各组电压之和。将各组灯丝电压代入上式得:
U\(_{G}\)=6.3V+6.3V+6.3V+6.3V+6.3V=31.5V
平均灯丝电流:
I\(_{G}\)=IG1+I\(_{G2}\)+…IGnn
式中I\(_{G1}\)…IGn为各组电流;n为组数。将各组灯丝电流代入上式得:
I\(_{G}\)=0.9A+0.65A+0.8A+0.6A+0.6A5=0.71A。
G=IG±I\(_{G}\)G%2。
式中G%为灯丝电压的变动率。因灯丝电流变动率为灯丝电压变动率的1/2,所以灯丝电流变动率为\(\frac{1}{2}\)ァ4肷鲜G=710mA±710mA×1;2×10%=710mA±35.5mA=674.5mA~745.5mA。
(2)求不加电感补偿时,灯丝最大电流I\(_{G不max}\)和应补偿的灯丝电流IG补。
I\(_{G不max}\)=IGminU\(_{max}\)Umin
式中I\(_{Gmin}\):灯丝平均最小电流;Umax:电源最高电压;U\(_{min}\):电源最低电压。将数值代入上式得:
I\(_{G不max}\)=674.5mA×\(\frac{240V}{180V}\)=899mA。
加电感补偿时,使原最大灯丝电流I\(_{G不max}\)降至灯丝允许的最大电流IGmax,它们的差值,就是由电感应补偿的电流I\(_{G补}\)。
故I\(_{G补}\)=IG不max-I\(_{Gmax}\),
I\(_{G补}\)=899mA-745.5mA=153.5mA。
(3)求最小磁化电流I\(_{Lmin}\)。为了使电感补偿取得一定的稳定性,最小磁化电流ILmin可取为应补偿的电流I\(_{G补}\)的1-1.5倍。若最小磁化电流选得过低时,会使电源电压超过最低允许值时,无稳定作用。若选得过大,使空载电流过大。这里取1.5倍为宜。
即:I\(_{Lmin}\)=1.5IG补I\(_{Lmin}\)=1.5×153.5mA=230mA。
(4)求最小总电流I\(_{总min}\)和最大总电流I总max。总电流由电阻分量电流和电感分量电流I\(_{L}\)组成。因为交流电流的合成,不仅与各电流大小有关而且与各电流的相位(方向)有关,因此用矢量图表示如图⑩。既表示出大小,又表示出方向。所以它们合成的总电流值I总=\(\sqrt{I}\)\(_{G}\)\(^{2}\)+IL2。
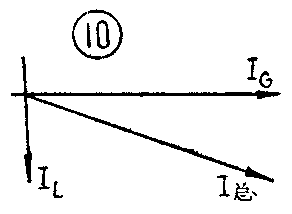
现已知最小磁化电流I\(_{Lmin}\)和最小灯丝电流IGmin数值,故可求出最小总电流I\(_{总min}\)
I\(_{总min}\)=\(\sqrt{I}\)Gmin\(^{2}\)+I\(_{Lmin}\)2
所以I\(_{总min}\)=\(\sqrt{(}\)674.5mA)\(^{2}\)+(230mA)2=713mA。
由最小总电流求出最大总电流
因为:I\(_{总max}\)=I总min\(\frac{U}{_{max}}\)Umin
所以:I\(_{总max}\)=713ma×\(\frac{240V}{180V}\)=950mA。
(5)求最大磁化电流I\(_{Lmax}\)。已知最大总电流和灯丝最大电流,按图⑩最大磁化电流应是最大总电流I总max和最大灯丝电流I\(_{Gmax}\)的矢量差值。所以:
I\(_{Lmax}\)=\(\sqrt{I}\)总max\(^{2}\)-I\(_{Gmax}\)2
I\(_{Lmax}\)=\(\sqrt{(}\)950mA)\(^{2}\)-(745.5mA)2=589mA。
(6)求谋戎岛腿范üぷ鞫巍
所以:589mA230mA=2.56
鸥杏η慷鹊谋涠担扔诘绺邢呷Φ拇鸥杏Φ缪棺畲蠛妥钚≈抵龋渲档扔诘扑孔芏说缪筓\(_{G}\)的最大和最小值之比。
所以\(\frac{U}{_{Gmax}}\)UGmin=(U\(_{G}\)+UG10%);(U\(_{G}\)-UG10%)
如用普通硅钢片作为电感的铁心,可在图⑧B~H曲线中求出工作段。
2.56:1=25.6~10安匝/厘米。
1.22:1=10600~8700高斯。
(7)求总圈数N。由于H的单位是安匝/厘米,表示每长一厘米的磁路,需10~25.6安匝。因此总磁化安匝等于H和磁路总长L的乘积。磁路总长可按图所示测量(图中虚线长度)。
这里所谓磁化安匝即电流与线圈的圈数乘积。所以圈数N等于磁化安匝除以电流。计算时,取最小或最大磁化安匝和磁化电流均可。这里取最小值。
N=H\(_{min}\)L/ILmin
如用GEI-14型硅钢片,磁路总长为10厘米。代入上式
N=10安匝/厘米×10厘米0.23安=434.8圈。
为了使各组抽头圈数相等,总圈数取组数n的倍数。这里取435圈,每组为87圈。
(8)求平均每伏圈数和铁心截面积S。平均每伏圈数等于总圈数N除以灯丝端电压U\(_{G}\)。灯丝端电压应和磁感强度B相对应,计算时取最大或最小值均可,这里取UG的最小值。
N\(_{0}\)=N/UGmin
N\(_{0}\)=\(\frac{435匝}{28.35伏}\)=15.3匝/伏
铁心截面积可按电磁感应公式求出。
S=\(\frac{4.5×10}{^{5}}\)B×N\(_{0}\)
式中B:磁感强度,单位是高斯。这里取与最低灯丝端电压U\(_{Gmin}\)所对应的最小磁感应强度Bmin。代入上式:
S=\(\frac{4.5×10}{^{5}}\)8700×15.3=3.4厘米2
(9)导线直径按下式求出:
d=0.8\(\sqrt{I}\)\(_{Lmax}\)ILmax:为线圈最大磁化电流,单位为安培。
d=0.8\(\sqrt{.}\)589=0.61毫米。
在铁心窗口面积允许的情况下,实际选择导线直径时,可尽量取大些,使稳压效果更好。
(10)串联电容C可按下式计算:
C=\(\frac{1}{2πfU}\)
C=\(\frac{10}{^{6}}\)314×U\(_{min}\)×I总min
所以C=
关于电感补偿器的调整
采用电感补偿后,降压电容C的选择也比较方便,可以控电容的产品系列选取,尽量减少并联电容数。如实际选用容量大于计算值时,可按图降低抽头联接;小于计算值时,可再增加些圈数。需增减的圈数可按下式求出:
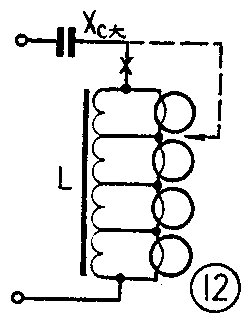
需增减的圈数=总圈数N(计算容量-实际容量)/实际容量
例如用10μf+4μf电容来代替12.6μf的电容使用时,代入上式:
需增减的圈数=435圈×12.6μf-14μf14μf=-44圈即需降低44圈处抽头联接。
如用10μf电容来代替12.6μf 电容使用,代入上式为113圈。则需增加113圈后联接,但增加部分的圈数导线直径应按总的最大电流I\(_{总max}\)来计算。
电感补偿元件接入线路时,如稳定电压范围过高,可拆去几片硅钢片或降低抽头位置联接,如过低时,可在电容C上,再并联一个小容量电容,使稳压范围合适。这种调整,对于按一定工艺生产的批量产品,稳定性能无明显差别,不必逐个进行调整。
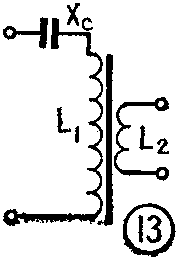
此外,电感补偿器还可以采用绕制次级线圈,供给整机的安全参考点使用,如图L\(_{2}\)。一般该绕组,可供给的功率等于初级线圈的ILmin×U\(_{Gmin}\)的20~25%时,不影响稳压性能。
电感补偿元件,用材料少,体积小,具有稳定容量大等优点。在稳压比与变压器相同时,其体积为相当的稳压容量变压器体积的1/30。若采用高导磁材料(如坡莫合金片)来制作电感补偿元件,体积更小。(完)(南京木器厂电视车间技术组 郑诗卫 韩惠仁)