(俞锡良)将放大器输出电路的信号,取出一部分又送回到输入电路,称为“反馈”。若反馈的信号电压与原来的输入信号电压相位相反,便叫做“负反馈”。因为负反馈有许多优越的特性,所以在收音机等设备中广泛采用。
一、负反馈的基本电路
若按从放大器输出端得到反馈电压的方法来说,可分为电压反馈和电流反馈两种基本类型,前者是反馈电压的大小随着载电压变化成比例地变化,后者则与负载电流的变化成比例。而从反馈电压送至输入电路的方式来看,又可分为串联反馈和并联反馈两种基本类型;前者是反馈电压与原来的输入信号电压相串联,后者则是相并联。以上四种最基本的电路,分别示于图1(a)(b)(c)(d)。在普通收音机内所常用的电路为(a)(b)(c)三种。
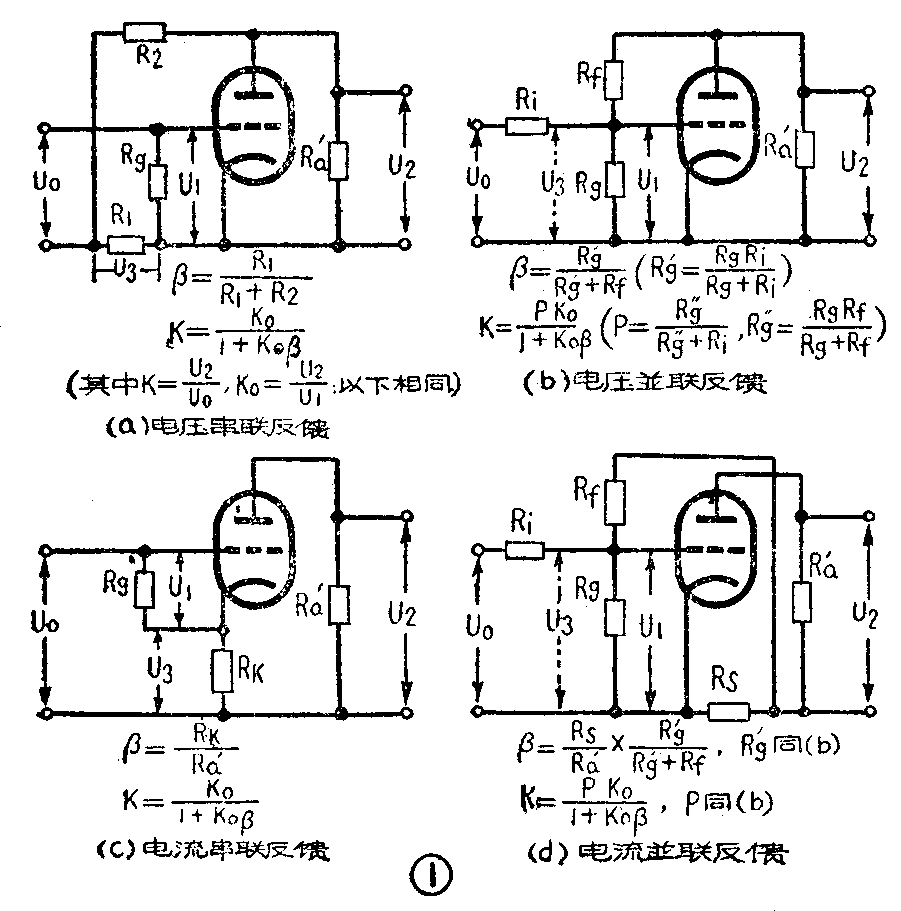
图1中,R\(_{g}\)为栅漏电阻,R'a为交流的等效负载,U\(_{0}\)为原来的输入电压, U1为实际输入电压,U\(_{2}\)为输出电压,U3为反馈电压。在(a)中,R\(_{1}\)和R2构成反馈回路,将输出电压分压后反馈到输入端。(b)中R\(_{i}\)为前级的内阻,反馈回路由Rf和R\(_{i}\)及Rg组成。(c)中R\(_{k}\)为阴极电阻,因没有旁路电容,屏流通过Rk时形成反馈电压。(d)的反馈电压先从Rs取出,然后再经过R\(_{f}\)和Ri及R\(_{g}\)的分压取得。
可以看出,在(a)(b)中反馈的电压是直接从负载端取出,与负载电压的变化成比例,而在(c)(d)中,则从屏流流过的电阻上取出,与负载电流的变化成比例。
从这些基本电路里,可以演变出其他较复杂的电路,如电压电流复合反馈和串联并联复合反馈等。此外,在一个放大器里也可能有好几个反馈环路,以及不同的反馈方式。
二、负反馈放大器的特性
1.增益降低,增益变化减小
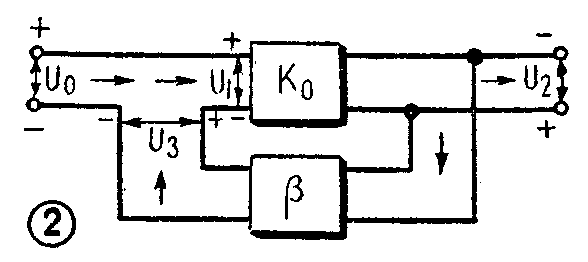
放大器的增益可以用输出电压对输入电压的比值来表示。为了分析方便起见,我们可以把反馈放大电路简化为图2形式。在没有反馈时,设输入信号电压为U\(_{1}\),输出电压为U2,那么增益
K\(_{0}\)=U2U\(_{1}\)……(1)
加上负反馈后,有效输入电压必定减小,很明显输出电压也要减小。如果要保持输出电压仍为U\(_{2}\),必须提高输入信号电压,使得输入信号电压减去反馈电压后得出的有效输入电压仍等于U1。设负反馈电压为U\(_{3}\),输入信号电压为U0,这时要求
U\(_{O}\)-U3=U\(_{1}\),
才能得到输出电压仍为U\(_{2}\)。因此,有负反馈时,输出电压对输入信号电压的比值为
K=\(\frac{U}{_{2}}\)U0……(2)
上面谈到,U\(_{0}\)必须大于U1,因此比较(1)式和(2)式,可以看出分子未变,K的分母增大,很明显K变小了,也就是说放大器在有负反馈时的增益变小了。
从(1)式和(2)式可得
U\(_{2}\)=K0U\(_{1}\)
U\(_{2}\)=KU0
所以
KU\(_{0}\)=K0U\(_{1}\)
或
K=K\(_{0}\)U1U\(_{0}\)……(3)
由于U\(_{1}\)=U0-U\(_{3}\),而负反馈电压U3为输出电压U\(_{2}\)的一部分,可以用U2乘一个分数β来表示,所以
U\(_{1}\)=U0-βU\(_{2}\)=Un-βKU\(_{0}\)=U0(1-βK)。
代入(3)式,得
K=K\(_{0}\)U0(1-βK)U\(_{0}\)=K0(1-βK)=K\(_{0}\)-βKK0
或
K+βKK\(_{0}\)=K0
K(1+βK\(_{0}\))=K0
所以
K=K\(_{0}\)1+βK0……(4)
一般β叫做反馈系数,βK\(_{0}\)叫做反馈因数。公式(4)表示有负反馈时与无负反馈时放大器的增益关系。图1中列出了典型电路中的类似关系式。
公式(4)很重要 从公式(4)可以看出,当β=0时,K=K\(_{0}\),这是没有反馈的情况。如果βK0远大于1,那么公式(4)分母中的1便可略去,从而得
K=K\(_{0}\)βK0=1;β
这就是说放大器增益只与反馈系数有关,只要反馈系数不变,放大器增益便能保持恒定。因此,在负反馈很大的时候,放大器增益便不致于因电子管特性、电源电压等稍有变化而变化,这是负反馈放大器的一个突出优点。这个优点从公式(4)已可看出。例如设
K\(_{0}\)=60,β=\(\frac{1}{30}\),得K=60;1+60\(\frac{1}{30}\)=20
如果K\(_{0}\)变化(更换电子管,电源电压变化等都可能引起K0变化),降低到30,β不变,得
K=\(\frac{30}{1+30}\)1;30=15
可见K\(_{0}\)减小1/2时, K只减小1/4,K的变化要小得多了。
公式(4)中的分母取对数乘以20,即叫做反馈量,用F表示:
F=20log(1+K\(_{0}\)β)…… (5)
反馈量用分贝计量,在设计计算时,常要用到。
2.失真和杂音的减小
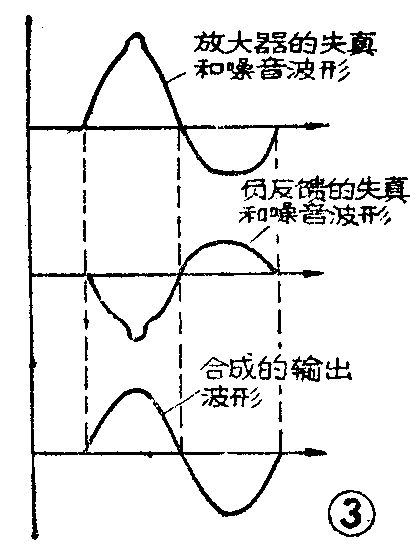
当放大器内部产生非线性失真和杂音时,因负反馈的波形相位相反,能起抵消作用,所以输出波形的失真与杂音能够减小,如图3。负反馈愈深,抵消作用也愈大。设U\(_{do}\)为无反馈时放大器内部的失真或杂音电压,Ud为有负反馈时输出的失真或杂音电压,则
U\(_{d}\)=Udo1+K\(_{0}\)β
即减小的倍数和增益降低的倍数一样。
如果输入信号本身已经失真或有杂音,就无法改善。此外,反馈电压的波形和输出电压的波形要完全相似,即反馈回路(或称“β回路”)本身不应该引起失真或杂音,否则,输出的失真和杂音不能减小,甚至增加。
3. 频率和相位特性的改善
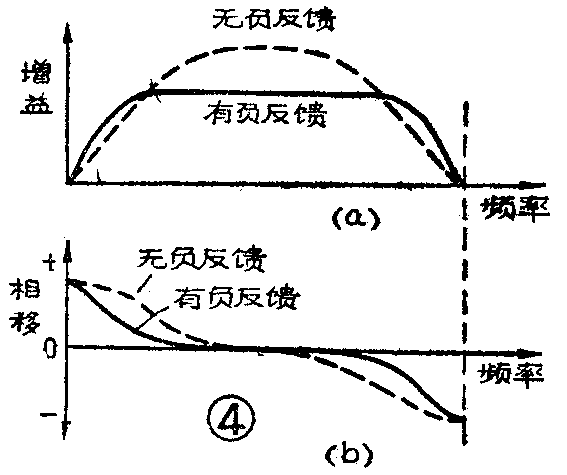
放大器在中音频率时,K\(_{0}\)较高,从公式(5)可看出负反馈量也大;但当高、低两端频率时,K0降低,负反馈量也减少,使K仍保持与中音频率时相近。所以放大器有负反馈后,频率特性变得平宽(图4a)。相位的变化与频率特性有关,频率特性下降的斜度愈大,相移也愈大,负反馈既使频率特性改善,则相移也能在较宽的频率范围内减少(图4b)。
放大器加入负反馈后,从整个电路来看,特性有所变化,故可用新的等效电子管参数和特性曲线来描绘负反馈放大器的工作。但是电子管本身的特性和工作状态并未改变,设计电子管的工作点和最佳负载等等仍和无负反馈时一样。最大输出功率也未改变。
5.输入阻抗和输出阻抗的变化
所谓“输入阻抗”,是指从放大器输入端看进去的阻抗,也就是输入信号电压与输入电流之比。在没有负反馈时,输入阻抗即是栅漏电阻等,而加入负反馈后输入阻抗则发生变化,它与反馈的输入方式是串联还是并联有关,而与反馈的输出方式是电压反馈还是电流反馈无关。在图1(a)(c)的串联输入反馈中,由于输入端引进了一个反馈电压,极性与输入信号电压相反,使输入电流减小,故输入阻抗变大。但若(a)的R\(_{g}\)接到R1的左边,或(c)的R\(_{g}\)下端直接接地,则输入阻抗与反馈无关,仍等于Rg,这在收音机中常是这样接法。在图1(b)(d)中的并联输入反馈时,由于输入端引进了反馈电流,且极性与输入电流同相,使输入电流增加。故输入阻抗减小。
所谓“输出阻抗”,是指从放大器输出端向屏极看进去的阻抗。设将输入端短路,假想在输出端拿掉负载,接入一个电压,向内流入一个相应的电流,输出阻抗就是这电压和电流之比。在没有反馈时,输出阻抗就是该级电子管的内阻。当加入负反馈后,则输出阻抗发生变化,它与反馈能量的输出方式有关,而与反馈输入方式无关。接入反馈电路后,输出端所加的电压有一部分反馈到输入端,经过放大又出现在输出端,在图1(a)(b)电压反馈时,这电压与上述假想接入的外加电压极性相同,使电流增加,故输出阻抗变小。在(c)(d)电流反馈时,极性相反,使电流减小,故输出阻抗增大。
收音机的负载是扬声器,输出阻抗愈小,则对扬声器的工作愈有利,发音愈清晰,故末级放大器最好采用电压负反馈,不宜用电流负反馈。
要计算收音机输出变压器次级扬声器端的输出阻抗Z'出,单级的情况可用下列的近似式:
当反馈只包括变压器初级
Z'\(_{出}\)≈\(\frac{n}{^{2}}\)S末β\(_{初}\)…………(6)
当反馈包括变压器次级
Z'\(_{出}\)≈\(\frac{n}{^{2}}\)S末β\(_{次}\)nη=n;S末β\(_{次}\)η……(7)
其中β初为反馈输入电压对初级的输出电压之比,β次为反馈输入电压对次级的输出电压之比。n为变压器次级对初级圈数比,η为效率。S末为末级管的互导。
如果反馈环内有二级或三级或更多级放大器,则公式(6)为
Z'\(_{出}\)≈\(\frac{n}{^{2}}\)K1K\(_{2}\)……S末β\(_{初}\),
(7)为Z'\(_{出}\)≈\(\frac{n}{K}\)1k\(_{2}\)……S末β\(_{次}\)η,
其中K\(_{1}\)K2……分别为第一级、第二级等的实际增益。要作较准确的计算时,还应把输出变压器内的电阻也包括在内,并且它的等效值亦与反馈有关。
6.负反馈放大器的稳定性
因放大器内有电容电感等元件,故会产生相移,频率愈到高、低两端时,相移也愈大。如果反馈量设计不当,在某些频率就会变成正反馈,甚至发生自激振荡而不能工作,必须加以注意,稳定性问题计算很繁,但可用实验调试。如果工作的反馈量与开始自激的反馈量之间相差6~10分贝以上,则放大器能稳定地工作。
三、常用的负反馈电路
1. 电流串联反馈
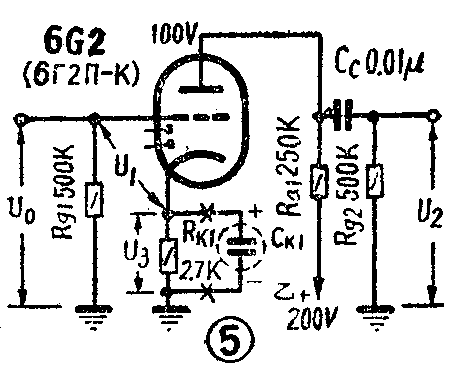
如图5,若把旁路电容器断开,便成为和图1(c)简图相似的电路,常用于电压放大器。不难算出,
β=\(\frac{R}{_{k1}}\)R'a=2.7;167=0.016,
其中R'\(_{a}\)为Ra1和R\(_{g2}\)的并联值。设旁路电容器未断开前的增益K0为54倍,则断开后的增益
K=K\(_{0}\)1+K0β=54;1+54×0.016=\(\frac{54}{1.87}\)=29
负反馈量F=20log(l+K\(_{0}\)β)=20log1.87=5.4分贝。
2.电压串联反馈
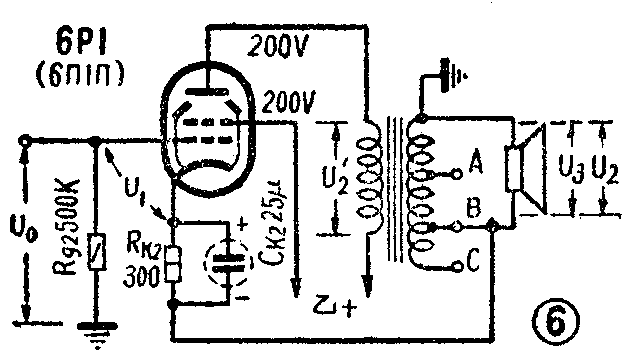
如图6,若把阴极电路接地点断开,通过输出变压器次级接地,并使极性为负反馈,即成为与图1(a)简图相似的电路,常用于简单的功率放大器。我们可以先算出至变压器初级端为止的有负反馈时的增益K,公式中的K\(_{0}\)为电子管输入至屏极输出的增益,而β初是nη,因为变压器的降压好比简图中电阻R\(_{1}\)和R2的分压作用。设K\(_{0}\)=22,n=0.029,η=0.75,于是
K=\(\frac{U'}{_{2}}\)U0=K\(_{0}\);1+K0β=\(\frac{22}{1+22×0.029×0.75}\)=22;1.48=15
反馈量F=20log(1+K\(_{0}\)β)=20log1.48=3.4分贝。
如果要求出次级的有负反馈时的增益K',则
K'=\(\frac{U}{_{2}}\)U0=K\(_{nη}\)=15×0.029×0.75=0.33
设电子管的互导为4.4毫安/伏,则次级的输出阻抗为
Z'\(_{出}\)≈\(\frac{n}{Sη}\)=0.029;4.4×0.75×10\(^{3}\)=8.8欧
我们也可以将输出变压器的×βnη包括在K\(_{0}\)之内,即公式中K0代以K\(_{0}\)nη;而β次为1,因U2全部反馈,没有其他分压。这样算出的结果和上面一样。如要增加反馈量,可在次级增加反馈圈数。
这种反馈方式也可在前级接入,反馈包括两级,所需的β可在变压器次级抽头调整。
3.电压并联反馈
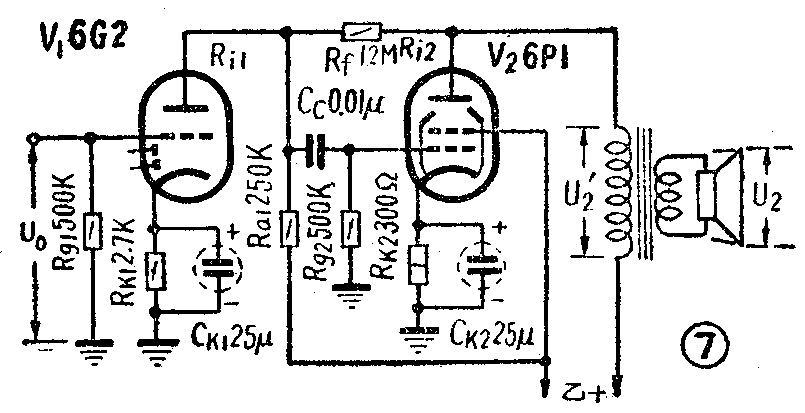
如图7,在两管之间接入R\(_{f}\),便构成与图1(b)相似的电路。这是一种常见的放大器电路。图1(b)中的Ri就是V\(_{1}\)的内阻Ri1,R\(_{g}\)则为Ral与R\(_{g2}\)的并联值,而U0则相当于V\(_{1}\)的等效电动势。设电子管参数与前一样,就可按图1所附公式求出β为0.044,以及末级电子管从输入到屏极输出在有反馈时的增益K2为11,F将为6分贝。
Z'\(_{出}\)≈\(\frac{n}{^{2}}\)S末β\(_{初}\)=4.3欧。
这种负反馈放大器的反馈量受到前级失真的限制,如不断加深反馈量,则由于末级输入阴抗减小而增益降低过多,要得到同样输出,就必须加大前级负担,结果末级失真虽很小而前级失真却大为增加,仍然得不偿失,此点需要注意。
4.电流电压串联反馈
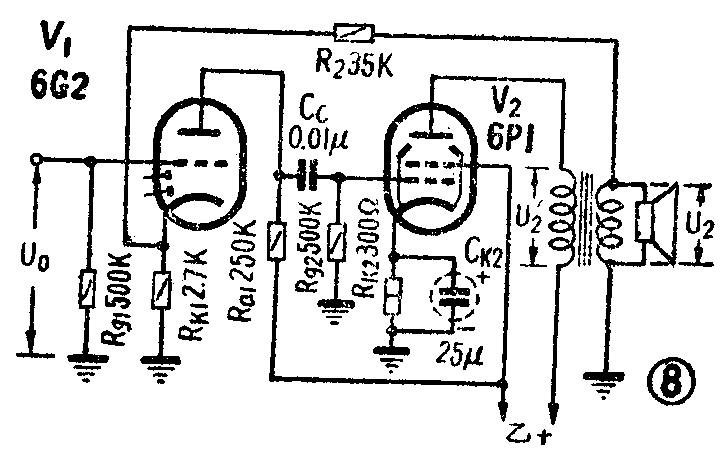
图8也是一种最常见的带负反馈的放大电路,其中共有两个反馈环:一是前级V\(_{1}\)本身的电流反馈;另一是末级V2的电压反馈。
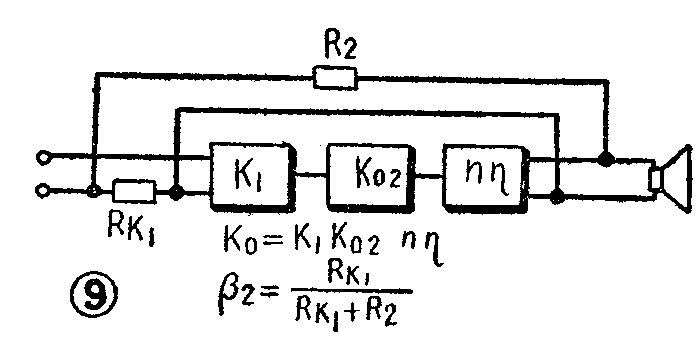
设电路元件数值和电子管的参数与前面例子相同。计算方法是先按前例算法解出有电流反馈时前级的增益K\(_{1}\)为29,F为5.4分贝。再将电路化为图9等效电路。求出
K\(_{0}\)=K1·K\(_{0}\)2·n·η=29×22×0.029×0.75=14
这时包括两级的电压反馈系数β\(_{2}\)为
β\(_{2}\)=RK1R\(_{K1}\)+R2=2.7;2.7+35=0.072;
所以
K=K\(_{0}\)1+K0β\(_{2}\)=14;1+14×0.072=7;
F\(_{2}\)=20log(1+K0β\(_{2}\))=20×0.3=6分贝
Z'\(_{出}\)≈\(\frac{n}{K}\)1S\(_{末}\)β2η=0.029;29×0.0044×0.072×0.75=4.3欧
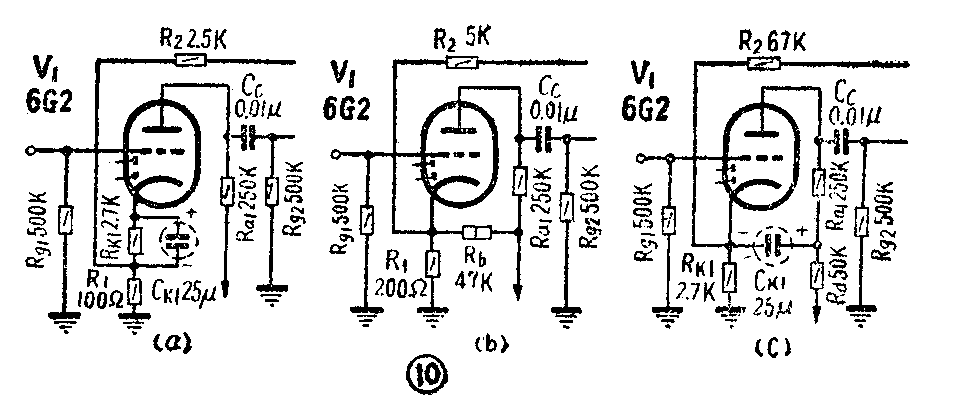
考虑到末级功率管的失真比前级大得多,故应加强末级的反馈量(即K\(_{0}\)β2要大)。在普通收音机里,放大器级数有限,要降低失真,同时又要兼顾增益较高,于是设法尽量减少前级的反馈量,把必要的反馈都加到末级中去。图10的三个例子都可达到这个目的。图10(b)的R\(_{b}\)为补足栅偏压之用。将前级电路稍加改变,使前级的电流反馈可以忽略,于是
K\(_{0}\)=K01·K\(_{0}\)2·n·η=54×22×0.029×0.75=26。
设F\(_{2}\)仍为6分贝,则
6=20log(1+K\(_{0}\)β'2)=20log2;
∴ 1+K\(_{0}\)β'2=2
K=K\(_{0}\)2=26;2=13。
与图8电路相比,因为F\(_{2}\)和前一样,且
Z'\(_{出}\)≈\(\frac{n}{K}\)01·S\(_{末}\)·β'2η=4.3欧,
故在失真和输出阻抗相似的情况下,增益却几乎提高了一倍。