一、问题的产生
在现代的自动电话、生产自动控制和远距离自动控制等设备中,常常使用大量的各种各样的继电器。有普通的线圈式继电器,也有电子继电器、热继电器和无接点的磁放大器式继电器等。这些继电器实质上就是一些开关,它按照所给定的条件使被控制的电路“接通”或“断开”。因此,所有继电器的共同特点是:启闭状态明显,变化突然,一般只有“启”和“闭”(或即“接通”和“断开”)两种稳定状态。由于这种原因,通常也把它们叫做双稳态元件。
继电器的作用虽然简单,但是要把许许多多的继电器组成一个电路,具有某种特定的功能,就不见得是那样容易了。
在本刊上一期“想想看”一栏中,曾提出这样的问题:要用两个开关互不相干地控制一个电灯。很多读者也许很快就会想出来,图1中所示的电路就可以达到这个目的。a和b两个开关,都可以随意接通或断开电灯X。
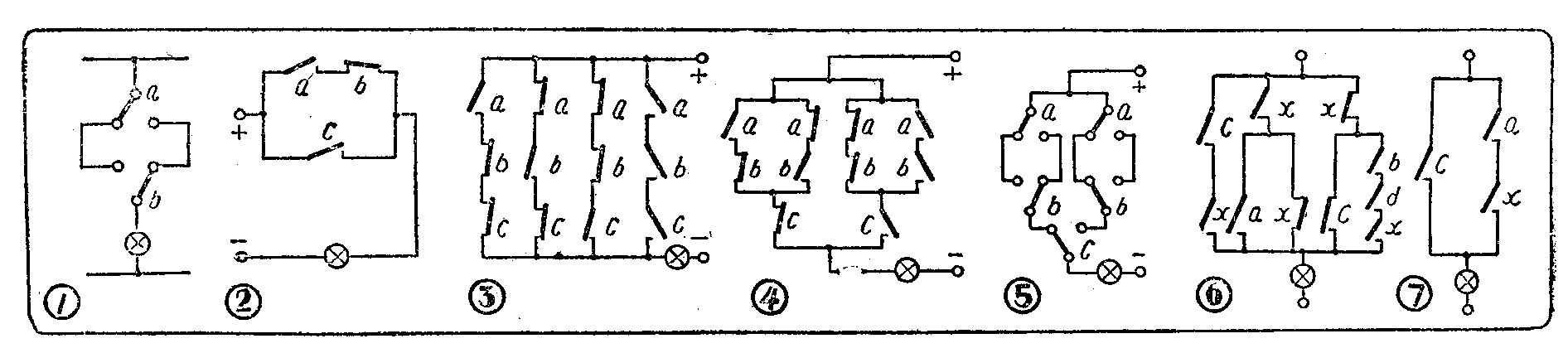
但是,如果我门要求有三个、四个或更多的开关都能独立地控制电灯X,那又该怎样办呢?读者不妨凭自己的经验构思一下这样的电路。这时你就会知道,由于仅仅多了一个开关,会使设计变得多么复杂。
在现代生产的大型自动化设备中,往往有成千上万个联接关系极为复杂的继电器。这时,按一般的直觉经验设计法来完成这样的设计任务,简直有不可想像的困难。因此,许多年来,很多学者一直在寻求继电器电路设计的数学方法。这种方法终于被找到了。这就是逻辑代数。逻辑代数在接点电路理论中又叫做接点电路代数或者开关代教,是目前研究接点理论的基本数学工具,它的实质,通过下面举的简单例子,是很容易了解的。
二、把接点电路写成数学式子
在逻辑代教中,首先要把逻辑关系转化为数学式子。
我们先看一下图2的接点电路。图中a、b、c分别表示三个继电器A、B、C(图中未画出)的接点,其中a和c是动合接点,而b是静合接点。由图可知,当

电路都可以接通,使执行元件或指示元件X工作。(结果)
前面这句话中的“与”、“或”、“不”(“否定”),就是逻辑代数中的三种基本运算形式。通常以乘号“×”代表连接词。“与”,以加号“+”代表连接词“或”,在运算对象的字母上面加一横代表“否定”。例如,若用a表示接点工作,则a-就“否定”了它的工作,即接点a不工作。
这样,若以F代表电路的工作条件,以X代表执行元件X工作,就可以把前面那句话写成以下的式子:
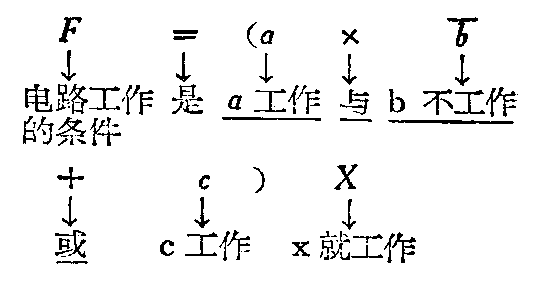
或者省去乘号,就得
F=(ab-+c)X。
这就是上述继电器电路的结构公式。如不写出X,即F\(_{x}\)=ab+c,就是元件X的动作公式。我们把这个式子和图2对照一下,就可以得出几条明确的规则:
1)乘号表示接点的串联,
2)加号表示接点的并联,
3)a,b,c……表示动合接合,
4)a-,b-,c-……表示静合接点。
有了这些规则,我们就不难根据电路的工作要求设计出所需要的接点电路来。
三、轻而易举的答案
现在让我们来设计一个“三开关控制一灯”的电路。这时,搬动开关的手就相当于一个继电器线圈。设它们的接点分别是a,b,c。电灯是信号元件,用X表示。要达到的目的是三个开关都能独立地控制电灯的明灭。
设a,b,c都不动作时,电灯是灭的。那么,当a,b,c中的任一个动作时,电灯都应该亮。在这种情况下,如果再使另一个开关动作,也就是使a,b,c中有两个动作时,电灯就应当灭。最后,再使第三个开关动作,即a,b,c都动作时,电灯又应该亮。由此可见,这个电路的条件是:当a,b,c都不动作或其中有任何两个动作时,电灯应当灭;当a,b,c中有任何一个动作或三个都动作时,电灯应当亮。由此可以写出:
当a动作与·b与·c不动作
或·b动作与·a与·c不动作
或·c动作与·a与·b不动作
或·a与·b与·c动作时
则电灯X(电路F)是接通的。
把上述条件按前节所述规则写成公式即为
F=(ab-c-+a-bc-+a-b-c+abc)X。
这样,就可以按前述规则画出我们所要求的电路,如图3所示。
由此例可以看出,逻辑方法如何使“多次试验”走向了一次成功。
四、接点数量的缩减 ——运算法则
图3的电路还可以利用逻辑运算的方法进一步化简。
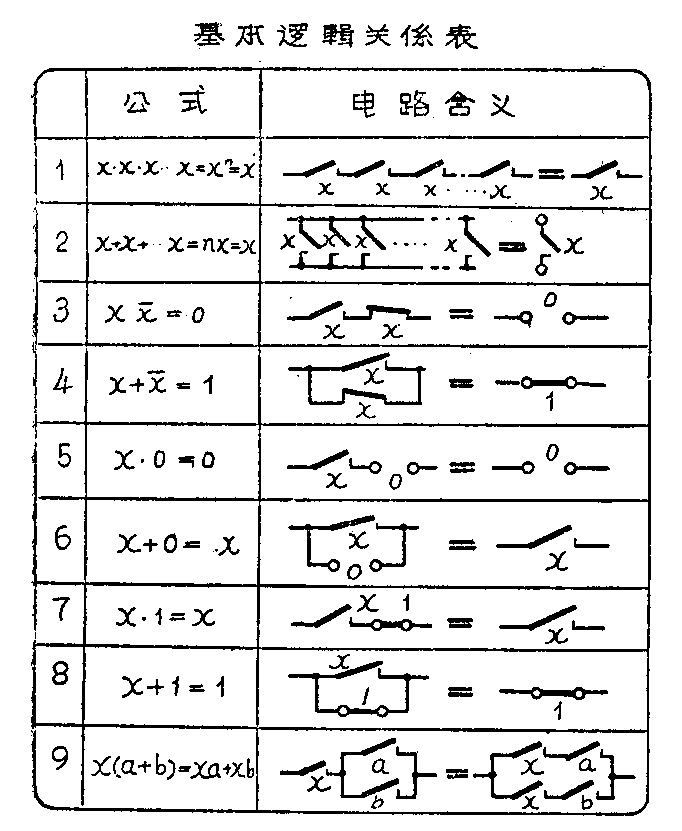
在设计实际的设备时,简化接点电路,缩减电路接点,不仅有很大的经济意义,而且对制造、安装、使用和检修都有很大好处,特别是可以提高设备的可靠性。在这个问题上,逻辑运算法给了我们很大的帮助。下面我们就来谈谈这种方法。
我们用“0”代表电路的断开状态,用“1”代表其接通状态,就可以得到前表所示的一些基本的逻辑关系式。
有了这些基本关系式,就可以根据电路的公式来简化电路。以图3的电路为例,电灯X的动作公式为:
F\(_{x}\)=ab-c-+a-bc-+a-b-c+abc
按表中公式(9),提出公因子c-和c,得
F\(_{x}\)=(ab-+a-b)c-+(a-b-+ab)c。
把这个结果绘成电路即如图4所示。然后,根据直观经验即可把图4电路化为图5的电路。由此可见,原来需要用三个四刀双掷开关的电路(图3),现在只要用两个双刀双掷开关和一个单刀双掷开关(图5)就行了。
我们再举一个利用上述法则简化接点电路的例子。要简化的电路示于图6。元件X的动作公式为
f\(_{x}\)=cx+x(a+x-)+x-(c+bdx)
=cx+xa+xx-+x-c+bdxx-。
因为xx-=0,
所以f\(_{x}\)=cx+xa+x-c
=c(x+x-)+xa。
因为x+x-=1,所以F\(_{x}\)=c+xa。
上式可画成图7所示的电路,它和图6的电路等效。由此可见,经过简化以后,接点数目大为减少。原来需要十付接点簧片,现在只需要三付就可以了。
五、在远距离控制中
现在我们用逻辑算法来研究一个远距离控制装置中常用的电路。在自动化生产中,常常要经过很远距离控制很多对象。但是为了经济起见,不可能使用太多数量的传输导线。在这种情况下,解决问题的方法之一就是应用相对少量的继电器的多种组合,来实现多个对象的控制。通常,一个继电器仅有“通”“断”两种状态,故只能实现一个对象的控制。但是两个继电器A和B就有“A通B通”、“A通B断”、“A断B通”、“A断B断”等四个状态组合(2\(^{2}\)=4),因而可以控制三个对象(因为有一个状态组合是对应于传输电路不工作的状态,即对任一对象都没有控制的状态,所以能控制的对象数为4-1=3)。不难看出,三个继电器能控制23-1=7个对象,四个继电器能控制2\(^{4}\)-1=15个对象。一般说来,n个继电器能控制N=2n-1个对象。例如,当有10个继电器时(n=10),能控制的对象数为N=2\(^{1}\)0-1=1023个。这就是说,用10条传输线(和一条公用地线),就可以控制一千多个对象。
作为一个例子,让我们来作这样一个设计:要求能按任何次序分别控制X\(_{1}\)、X2、X\(_{3}\)、X4、X\(_{5}\)、X6、X\(_{7}\)等七个对象。试求所需的继电器数,并绘出电路接线图。
解:1.根据公式N=2发\(^{n}\)-1,代入被控制对象数N=7,便可求得n=3。
2.求电路。
设A、B、C为三个继电器,其接点分别为a、b和c。由于每个继电器都有“工作”和“不工作”两种状态,故三个继电器就有8种状态组合,即:
1)abc,2)abc-,3)ab-c,4)ab-c-,5)a-bc,6)a-bc-,7)a-b-c,8)a-b-c-。
令第8)状态为零状态,即控制对象都不动作的状态,而其它七种状态分别为使七个被控制元件X\(_{1}\),X2,……X\(_{7}\)动作的状态,则可把七个被控元件分别串联在上述七种状态的电路中。于是得出继电器电路的总方程为
F=abcX\(_{1}\)+abc-X2+ab-cX\(_{3}\)
+abc-X\(_{4}\)+a-bcx5+a-bc-x\(_{6}\)
+a-b-cX\(_{7}\)
=a(bcX\(_{1}\)+bc-X2+b-cX\(_{3}\)+bc-X4)
+a-(bcX\(_{5}\)+bc-X6+b-cX\(_{7}\))
=a〔b(cX\(_{1}\)+c-X2)
+b-(cX\(_{3}\)+c-X4)〕+a-〔b(cX\(_{5}\)
+c-X\(_{6}\))+b-cX7〕。
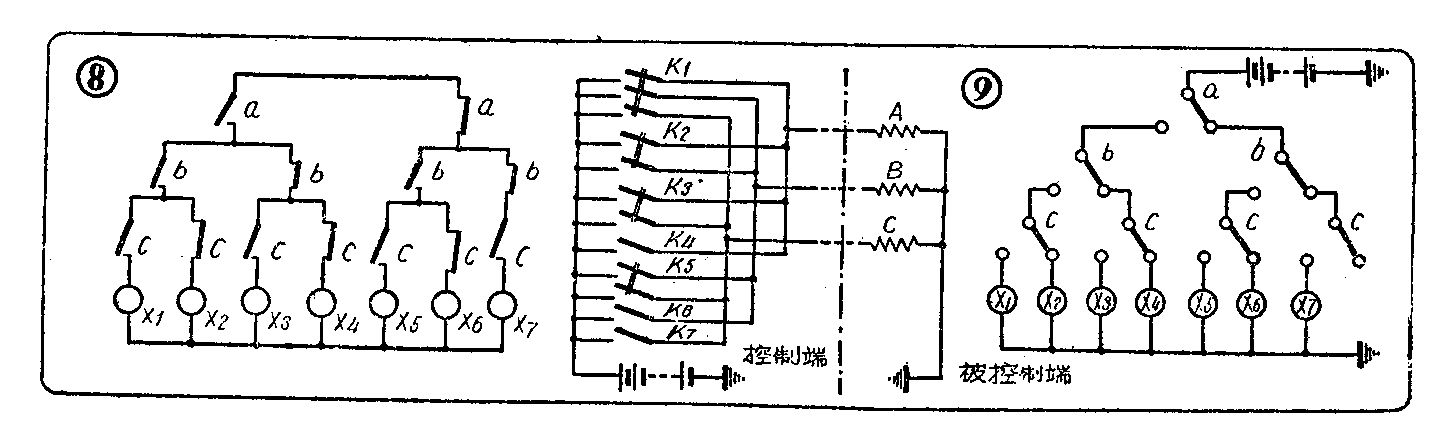
此结果可绘成如图8所示的接点电路。然后,根据三个继电器状态组合的关系,可以在控制端组成开关K\(_{1}\)、K2……K\(_{7}\)等,即得能实际应用于遥控的一套电路,如图9。由图可知:
按下K\(_{1}\), a,b,c,动作 X1工作,
按下K\(_{2}\) a,b动作 X2工作,
按下K\(_{3}\) a,c动作 X3工作,
按下K\(_{4}\) a动作 X4工作,
按下K\(_{5}\), b,c动作 X5工作,
按下K\(_{6}\) b动作 X6工作,
按下K\(_{7}\) c动作 X7工作。
这样一来,我们总共只用了三根传输线,就能控制七个元件的动作。
从上边所介绍的一些例子可以看到,利用逻辑代数来研究和设计电路是很方便的。但是,这里所谈的只是一些最简单的情况。实际上常常应用到延时的、快吸慢放或慢吸快放的等等多种形式的继电器,它们常组成所谓多步电路,即按一定顺序自动动作的继电器电路。在这种情况下,就要用到更多的逻辑理论公式,同时逻辑设计的优点也就表现得更为明显了。(田进勤)