(本文系供水平较高的工程技术人员参考——编者)
调节天线方向图,可以减少必须的天线数目,提高运用率,降低维护费用。
如众周知,利用对天线的每半边以不同相位馈电的方法,可以使CГ型天线方向图主瓣最大值偏位达15°。较大角度的方向图偏位不予采用,因为当相移超过90°时(相当于偏位15°),旁瓣将显著地增加。具有特殊天线转换器的CГ-P型天线,由于将天线网及反射器转接,可以使方向图转180°。
本文讨论±15°范围内的偏位问题,因为180°的偏位并不特别困难,仅与拟定妥善的天线转换器有关。
图1示能使天线方向图偏位的电路图,偏位所必需的相移可以由改变半边天线Ⅰ及Ⅱ的配电馈线PФ的长度来得到。改变主馈线ГФ的连接点使二半边天线间的电流发生相移,因而引起主瓣最大值偏位。
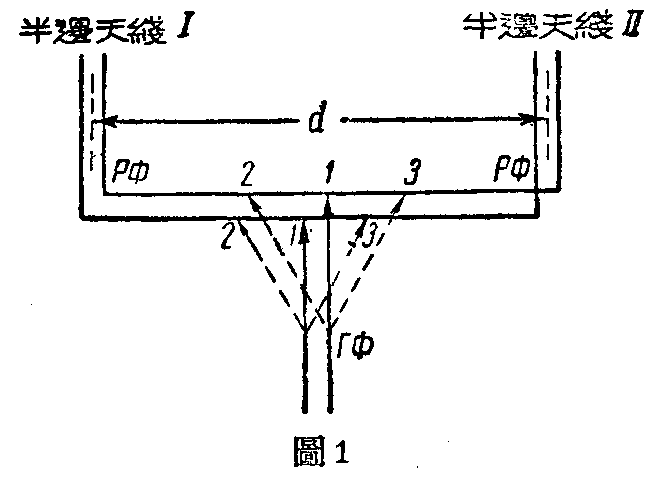
如果已给主瓣最大值的偏位角,则所需的相移角可以由下式计算:
ψ=mdsin m (1)
式中m=2πλp——波数,λp——工作波长,d——二半边天线中心间的距离(参看图1)。
虽然上式没有考虑影像的影响,但它测量的结果完全吻合。
行波时,为了获得预定相移所必需的配电馈线长度差,可按下式计算:
Δl=\(\frac{ψ}{m}\), (2)
式中 Δl——配电馈线的长度差。
但是在大多数情况下行波系数K小于1,此时Δl按下式计算:
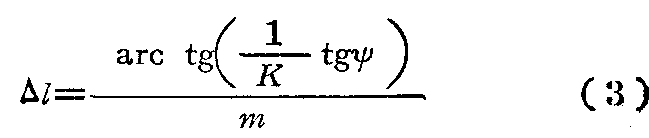
如果Δl值为已知,则此时的相移可以按下式计算:
ψ=arc tg(KtgmΔl) (4)
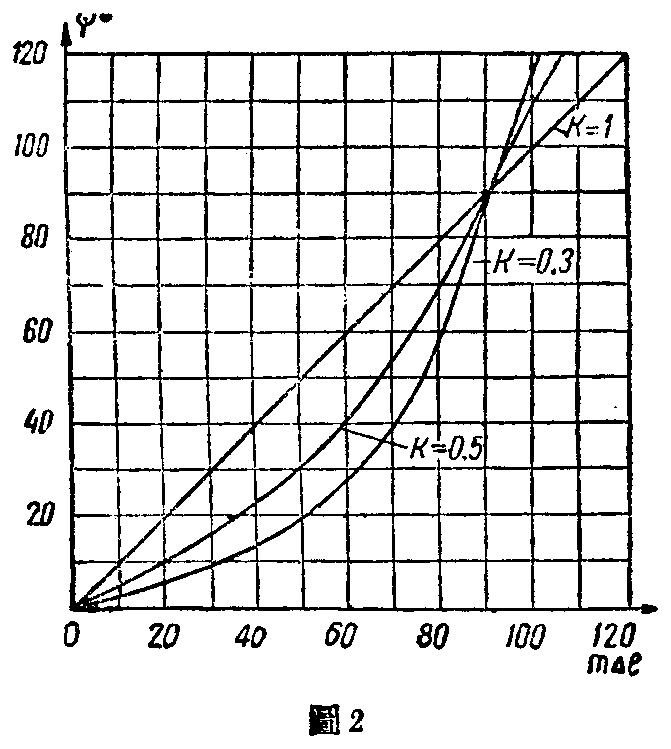
mΔl称为馈线的电长度差。各种K值时ψ与电长度差mΔl间的关系列于图2。如果行波系数小于1,则在半边天线Ⅰ和Ⅱ之间功率的分配可能不相等。
二半边天线辐射功率的比率a由下式确定:
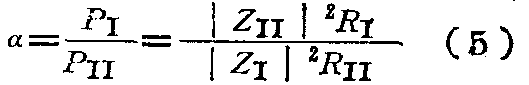
式中P\(_{Ⅰ}\)及PⅡ——分别为半边天线Ⅰ及Ⅱ所辐射的功率,|Z\(_{1}\)|及|Z2| ——半边天线Ⅰ及Ⅱ的配电馈线在连接主馈线处的输入阻抗的模数,R\(_{Ⅰ}\)及RⅡ——输入阻抗的有效部分。
从公式(5)可以看出,如果将二半边天线的输入阻抗认为是相等的,则当主馈线ГФ接点1—1时(图1),电功率将平均分配于二半边天线内,因为此时Z\(_{Ⅰ}\)=ZⅡ。但是,如果K<1,则当主馈线接至点2—2或3—3时,Z\(_{Ⅰ}\)≠ZⅡ,因为当计算二半边天线在和主馈线连接处的输入阻抗时,将牵连到配电馈线的电长度差。
当Z\(_{Ⅰ}\)及ZⅡ为各种不同的数值时,电功率平均分配的条件可以写成下列形式:
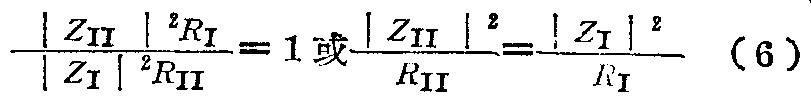
实际上最有用的情况乃是当二半边天线间的相位差等于90°,即当方向图发生15°偏位时,此时为了获得90°相移所必需的电长度差mΔl,与行波系数无关,并也等于90°,即Δl=\(\frac{λp}{4}\),而点1—1与2一2及点1—1与3—3之间的距离等于λp;8。
为了求出当Z\(_{Ⅰ}\)及ZⅡ为各种不同的数值时,二半边天线间电功率是怎样分配的,让我们研究两种极端情形。在第一种情况下,我们假定点1—1处发生电压波节或波腹(当K<1),在第二种情况下,假定电压波节或波腹位于距离点1—1λp8的地方。
从长线理论得知,线长λp8的输入阻抗等于
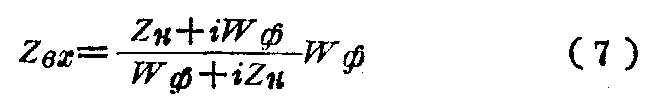
式中Z\(_{бх}\)——线路的输入阻抗,Z——线路始端的阻抗,Wф——线路的波动阻抗。
利用公式(7)可以求出为了计算二半边天线间功率分配情况所必需的Z\(_{Ⅰ}\)及ZⅡ。设发生第一种情况,我们假定电压波节位于点1—1处,而主馈线接至点2—2,此时相当于使方向图,顺时针方向转15°,为了计算Z\(_{Ⅰ}\)把\(\frac{Wф}{K}\)代入公式(7)替换Zн:
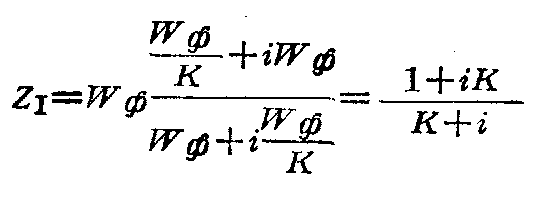
为了确定Z\(_{Ⅱ}\),把WgфK代入公式(7)替换Zн。此时相当于在半边天线Ⅱ那边距点2—2λp8处为电压波节:
Z\(_{Ⅱ}\)=\(\frac{K+i}{1+iK}\)Wф
此时Z\(_{Ⅰ}\)及ZⅡ满足电功率平均分配的条件[参看式(6)],即
α=\(\frac{P}{_{Ⅰ}}\)PⅡ=1 K为任何数值。
对于第二种情况,利用公式(7)及(6),则得
Z\(_{Ⅰ}\)=\(\frac{Wф}{K}\),ZⅡ=WфK及α=P\(_{Ⅰ}\);PⅡ=K\(^{2}\)。
相当于第二种情况的电压分布状况示于图3б,此时假定电压波腹位于点2—2及点3—3。
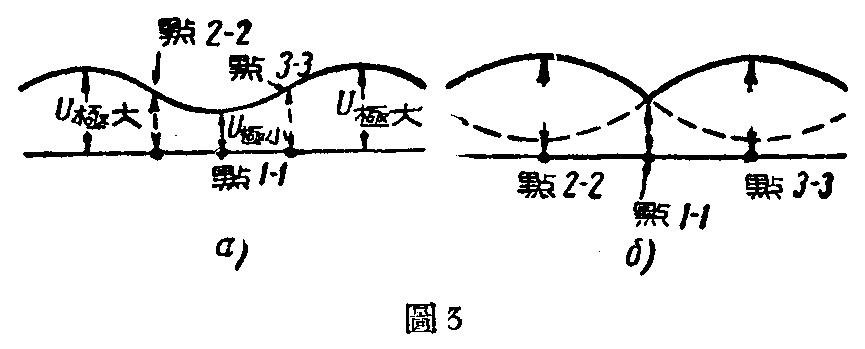
显然,在上述情况中电功率的分配与配电馈电线上的行波系数有着密切的关系。功率的不平均分配使得方向图扩张、减少偏位角 \(_{m}\)并增加旁瓣,由于方向图扩张及旁瓣增加天线的增益系数降低。
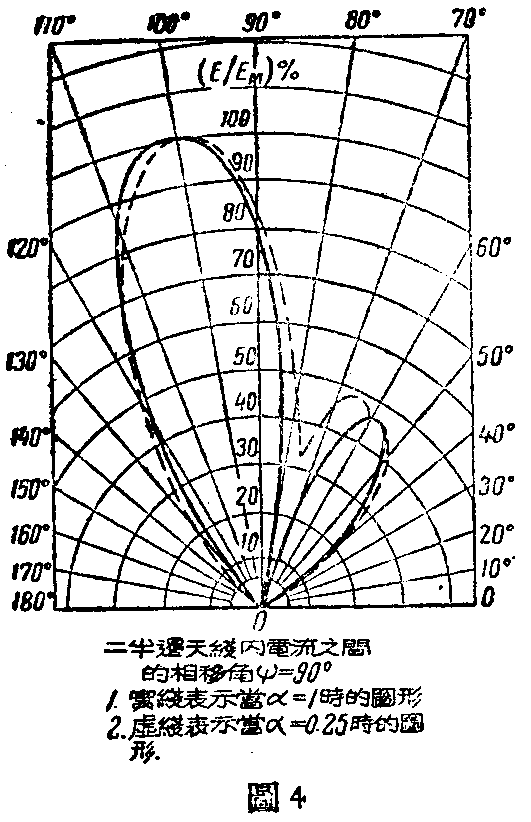
为了比较起见在图4上绘出了当α=1及0.25时四个振子排成一行的CГ型天线在其水平面内的方向图,这些图形系由下式求得:
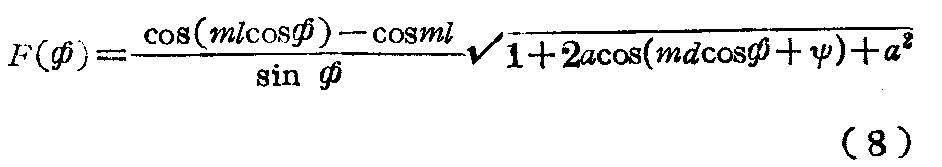
式中a=\(\sqrt{α}\)=K——在已知的功率分配情况下由每半边天线所产生的场强比值。
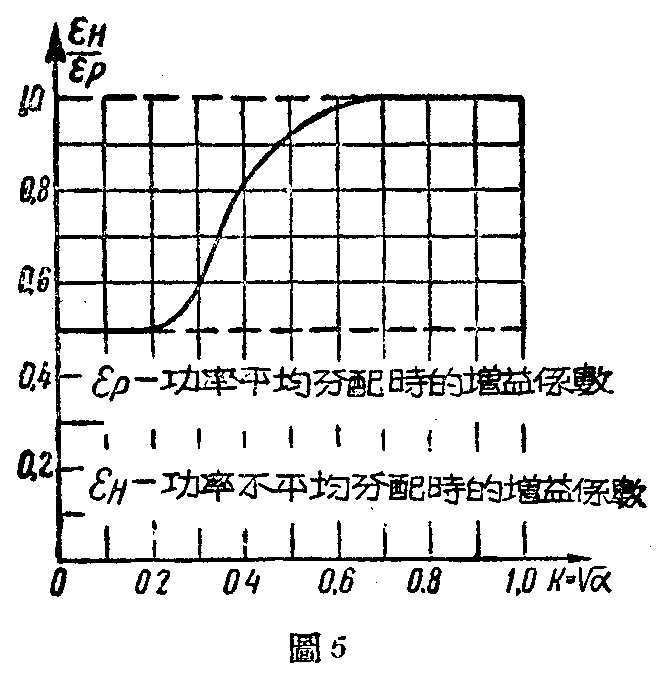
增益系数随功率分配变化的曲线示于图5,从曲线可以看出只有当K小于60%时,天线增益系数才由于功率分配不均匀而发生显著的降低。必须补充说明,计算方向图及增益系数时,没有计及影像及二半天线之间的影响,事实证明这样作是完全容许的。
让我们来研究主馈线与配电馈线相匹配的问题,通常希望主馈线及配电馈线的K值相等。为了达到这个条件,主馈线的波动阻抗应当是配电馈线波动阻抗的二分之一。当配电馈线的输入阻抗Z\(_{Ⅰ}\)及ZⅡ相等时,主馈线的行波系数将等于配电馈线的行波系数。
前面已经指出,如果K<1则仅在点1—1处,Z\(_{Ⅰ}\)=ZⅡ。因而当在方向图偏位的情况下工作时,主馈线与配电馈线的行波系数将不等。但是从下述的计算得出主馈线行波系数Kιл永远大于或等于配电馈线行波系数K。
我们来确定与上述同样的功率分配情况下的Kιл值。
第一种情况:
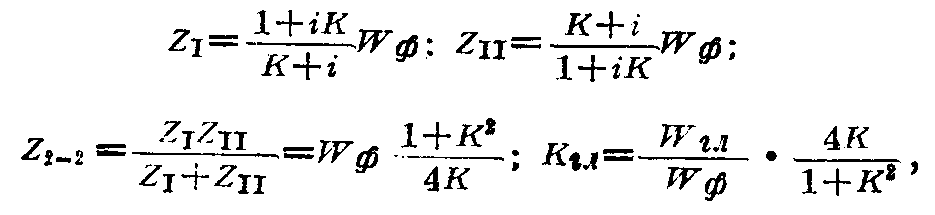
式中Wιл——主馈线的波动阻抗。
如果能够使得Wιл=\(\frac{1}{2}\)Wф,则Kιл=2K;1+K\(^{2}\),即当0≤K≤1时,Kιл≥K。
第二种情况:
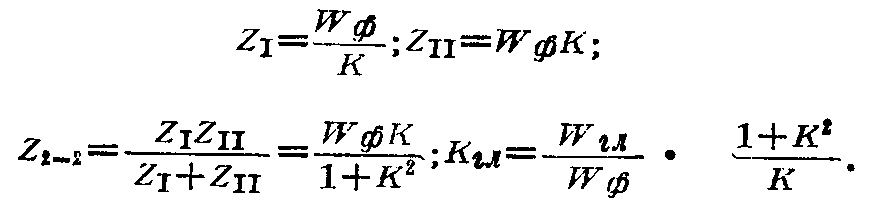
当0≤K≥1时,同样Kιл≥K。例如,如果K=0.5,则在两种情况下,Kιл均等于0.8。
因此,在这些场合下当方向图偏位时,主馈线与配电馈线的匹配得到改善。但是必须注意,当主馈线接至点1—1及2—2或3—3时在主馈线上的电压分布将不同(当K<1)。
由于当电压分布改变时,即当波腹的位置及Kιл值改变时必需达到应有的匹配,我们采用调整设备以调谐主馈线。在许多情况下为了调谐可以利用所谓“四分之一波长配接线”。
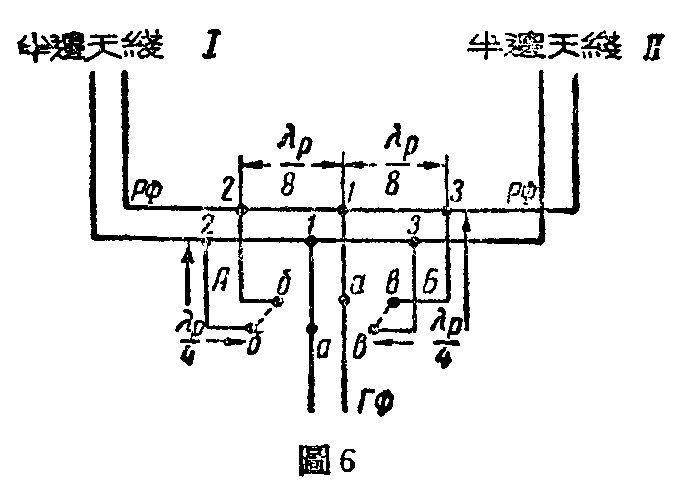
最后让我们来研究最广泛采用的方向图偏位电路图(图6)。主馈线ГФ,其终端为a—a点,藉桥接线A及B可以任意接至点1—1或接至点B—B或点(B—B)。使桥接线的波动阻抗等于Wιл ,桥接线A及B的长度为\(\frac{λp}{4}\),同时在点B—B及B—B将不工作之桥接线短路。在此情况下接线在点2—2及3—3的输入阻抗值非常大,因而它们对配电馈线及主馈线的匹配并不发生任何显著影响。
根据以上的分析可以作出下列的结论:
1.当K远小于1时上述方向图偏位电路图仍可正常工作。勿需将每一配电馈线调至行波状况。
2.选择配电馈线的长度使在点1—1发生电压波节或波腹可以使得二半边天线间功率的分配平均。
3.当K>60%时,功率的不平均分配几乎对天线的工作不发生影响。
4.Kιл≥K;当主馈线接至点1—1或2—2及3—3时主馈线调谐时必须考虑Kιл的变化及在主馈线上电压的分布情况。((苏联)无线电企业工程师P.B.顾烈维奇原著 萧笃墀编译)
(原文载1954年第7期苏联邮电公报)