巧用Excel解方程
软件世界
解方程是我们经常遇到的数学问题。有些方程可以求出解析解(比如一元二次方程有求根公式)。而有的方程很难求出或根本没有解析解(如ex-x-2=0这类方程就没有解析解)。对这类方程,通常我们可用编程或用专门的数学软件求它的数值解。可是如果不会编程又没有专用软件那又怎么办呢?
下面就以方程ex-x-2=0为例,介绍一种用Excel求方程数值解的方法。
首先,要把方程变换成x=f(x)的形式。这里,我们把上面的方程写成x=ex-2的形式。然后,新建一个工作表,在B2单元格内输入-2作为初值,在B3单元格内输入公式“=exp(B2)-2”,把鼠标放在B3单元格右下角的小黑方块上向下拖动,一直填充到B16单元格。我们可以看到B3至B16单元格内的数字逐渐趋于一个稳定的值,这个值就是方程的一个根。
有读者可能要问:我怎么知道应该选多少作为初值呢?别忘了,Excel有绘图功能。可以先绘出y=ex-x-2的函数图像,曲线与x轴的交点就是方程ex-x-2=0的解。从(图1)中看出,在-2附近有一个根,所以上面我们把-2作为初值。
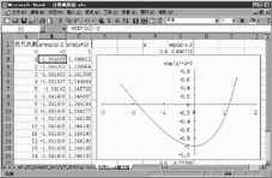
从(图1)中还可以看出,这个方程还有一个根在1附近,可是不论我们怎样改变初值都无法得到1附近的这个根。要得到这个根需要修改迭代公式。把原方程写成另一种形式x=ln(x+2),在C2单元格内输入1作为初值,在C3单元格内输入公式“=ln(C2+2)”,把鼠标放在C3单元格右下角的小黑方块上向下拖动,一直填充到C16单元格。至此,我们得到了这个方程的全部两个根-1.841和1.146。
上面所用的求数值解的方法叫做迭代法。即给定一个x的初值,将它代入x=f(x)的右边,得到一个数值,再将得到的结果代入f(x),如此反复,得到的x值就会越来越精确。在这个例子中,经过10次迭代所得到的数值已经相当精确了。这个方法对大多数方程是有效的,但有时迭代会出现发散或振荡的情况,这时可以换一个初值或者换一个迭代公式试试。读者如果想了解更多的关于迭代法的知识,可以参考数值计算方面的书籍。