为了加强对欧姆定律概念的理解,我设计了图1所示的简单实验电路。我的目的是要证明当电源接通后,串联电阻R1和R2上的电压降应该相等,且其和应该等于电源两端的电动势E。为此我用了一个新电池作电源,选了两个阻值相同的l0kΩ电阻作R1和R2。接通电源后,把一只袖珍万用表正确地拨到直流电压挡上,为了把读数看得更清楚些,把量程拨在满度2.5V挡上。然后就分别测量两个电阻上的电压降U1和U2。
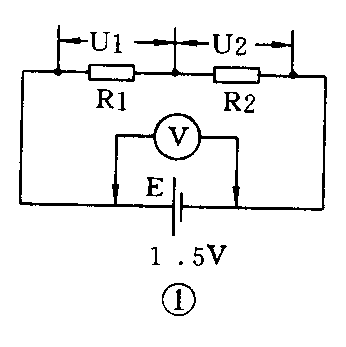
不错,两个电阻上的电压降是相等的,即U1=U2,其读数都是0.54V。然后我再去测量电池两端的电压,即电池的电动势,结果显示为l.5V。简单一加,不禁令我感到奇怪:0.54V+0.54V=l.08V。怎么不是1.5V呢?所短缺的0.42V(1.5-1.08=0.42)到哪里去了呢?
我怀疑什么地方弄错了,便再三检查电路,校对万用表,并三番五次地重复试验,结果除了因为读数有一点点视觉误差之外,确实没有任何错误。百思不得其解的情况下,我去请教了一位老无线电爱好者,我叫他“古老师”。他听完后只作了一点简单的计算,就告诉我说:“测量没错,读数也对,万用表也没问题。问题出在测量观念上!你要是用10V挡去测量,就不会有那么大的误差了。”
古老师是这样分析和解答这道“怪题”的:首先他把原图细化为图2的形式,目的是在电路中体现出万用表的内阻对电路实际状态及测量结果的影响。他假定万用表的内阻为R0,因此当用这只万用表去测量任何一个电阻上的电压时,被测电阻的真正值都不再是原来的l0kΩ,而是原来的10kΩ与电表内阻R0关联起来的总电阻。这个总电阻肯定比10kΩ小,且以R′来代表,则有:R′=R2×R0/(R2+R0)或R′=Rl×R0/(R1+R0)
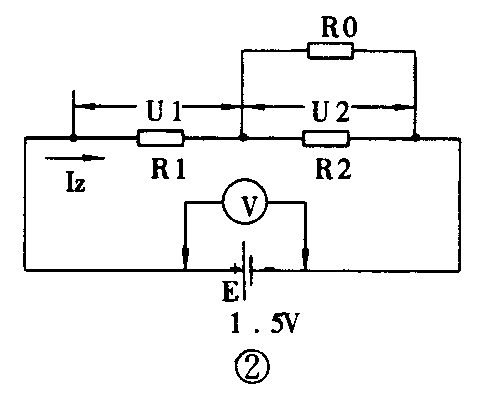
因为R′<R1或R2,所以测量时所得到的读数U1或U2肯定不是电池电动势的一半,而是要比它小。还记得吗?我把我测量的结果U2=0.54V告诉了古老师,所以他就用上面的公式来推算R0的数值。其实你和我也能独立地完成这个计算。
既然E=1.5V,而所测电阻R2上的电压降为0.54V,那么另一个电阻R1上的电压降就必然是l.5V-0.54V=0.96V,于是流过电路的总电流就是Iz=0.96V/10kΩ=0.096mA了。
另一方面,此时从R2及R0上流过的电流总和也应该是Iz=0.096mA。因为R2是已知的(=10kΩ),所以从它上面流过的电流肯定是I\(_{R2}\)=U2/R2=0.54V/10kΩ=0.054mA。那么还有0.096-0.054=0.042ZmA的电流自然就从电表内阻R0上流过了。由此便可求得R0的阻值为R0=0.54V/0.042mA≈12.86kΩ。因为我当初测量时是把电表拨在2.5V挡上的,所以古老师便可据此算得我用的是5kΩ/V的表头:
12.86kΩ/2.5V≈5kΩ/V。
一看这个数据,我想你也会和我一样豁然开朗:把一个12.86kΩ的电阻并联到l0kΩ电阻上面去了,阻值几乎减小到一半,测出来的电压不变低才怪了呢!
话说回来,既然表头的内阻参数是5kΩ/V,如果放在10V挡上,则总内阻就变成了50kΩ,把它并联到l0kΩ的R1或R2上面去时,其影响比起12.86kΩ来自然就要小得多,难怪古老师建议我用10V的量程来测量。
既然选用的量程越大,则万用表内阻对被测电路的影响就越小,我们何不用50V的量程或更大的量程来测量呢?当然也不行,因为此时指针摆动的角度将大大减小,能读出的电压精度也就大大减低了。理想的办法是换一个灵敏度较高的电表,即每伏欧姆数较高的万用表来测量。例如每伏50kΩ或100kΩ的指针式万用表,或者目前流行的任何一种数字万用表。(顾亭)