在学习电子技术的基础理论时,不少初学者往往只注重单纯记公式、做习题,却忽略了公式所包含着的基本概念。在分析问题和解决问题时往往乱套公式,没有真正懂得表达定律和定理的公式中,各个量的概念及相互之间的关系。这就难免会出错误。
有这样一个习题:“将6V电压加在某电器两端时(见图1),通过它的电流强度是100mA,问电器的电阻是多少?又问当电压变为0V时,它的电阻又为多少?”前半题按公式R=U/I,不难求得电器的电阻为60Ω。后半题如果疏忽概念直接去代公式,会得出电器电阻为0Ω的结果,显然不符事实。错在哪里呢?我们还是从欧姆定律中去找答案。欧姆定律是这样说的:“通过一段导体的电流强度和导体两端的电压成正比。”写成等式为I=U/R或U=IR。式中I和U可以是变量,但电阻实际上是一个常量。在公式中,它是电压和电流的比例常数,其大小不由电压和电流决定,而是与构成电阻的材料和几何形状有关。其中电阻值R与材料的长度L成正比,与横截面积S成反比。用公式表示:R=ρL/S,式中ρ为电阻率,其大小由材料决定。一旦电阻值确定后,把它接在电路中可以改变或影响电流及电压的值,而电流或电压却不能改变电阻的值。
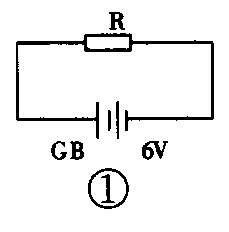
电阻在电路中是个耗能元件,有阻碍电流流动的本性。电流通过电阻要消耗电能。沿电流流动方向必然会产生电压降,其值为电流与电阻的乘积。对于一个有确定值的电阻,它两端所加电压越大,流过该电阻的电流也越大;反之,它两端所加的电压越小,流过电阻的电流也越小。总之,电压和电流的比值总是一个恒量,即已确定的电阻值。即使电压为零,电阻值仍然以它的原有值存在着,要不然上述习题中的用电器的电阻值就变成不存在了。在习题中我们虽然可以用数学公式的可逆性,以R=U/I来求出未知用电器的电阻值,但是欧姆定律的概念却万万不能用数学公式R=U/I来逆向叙述。否则欧姆定律会成为:导体的电阻,跟它两端的电压成正比,跟通过它的电流成反比的错误概念。
正确理解电子技术中的基本概念和基本规律,可以提高我们分析问题和解决问题的能力。概念是从大量的实践中抽象、概括出来的反映事物本质属性的思维形式。而公式则是用数学形式表示定律和定理中各个量之间一定关系的式子。概念可以通过公式来表示,但公式不能完全替代概念。与电阻元件常在一起工作的电容器,也是电子技术中最基本的元件。提起它,初学者自然会想到公式C=Q/U,即电量/电压。我们不妨再来做一个习题:“有一个电容器,带电10\(^{-5}\)C时,电压是200V,如果它的电量再增加10-3C,这时它的电压是多大?在这个过程中电容器的电容变不变?等于多少?”解题前我们还是先来看看电容的概念吧:“对于一个电容器,它的电量跟两极板间电势差是成正比的,它们的比值叫做电容。”即随着电量Q的增加,电势差U将按比例地增加,Q与U的比值是一个常量,即电容。它的物理意义是使导体每升高单位电位所需的电量。与电阻相似,电容的大小与电容器的结构、形状和极板间介质有关,而与带电多少无关。一旦电容的结构、形状和介质确定后,其电容量也就确定了。电容大表示每升高一个单位电压时,所需增加的电量也多。好比盛水的容器,不同体积大小的容器,灌入相同高度的水量是不同的(见图2)。容器小的所需的水量少;容器大的所需的水量多。对于容器来讲,即使不灌入求其容量还是客观存在的。电容器与此类似。
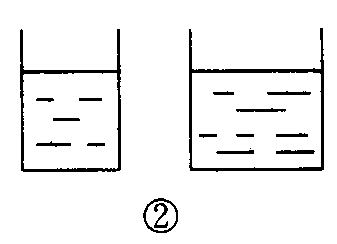
电容器在电路中有储存电荷的作用,因而称它为储能元件。由概念可知,一个电容器两端所加的电压越高,聚焦的电荷也越多,即电量Q越多。明白了电容的概念后不难求出习题中的电容值:C=10\(^{-}\)5/200=5×10-8(F),增加10\(^{-3}\)C后电压为2.02×104V,整个过程中电容器的电容量是不变的。为了加深读者对电容概念的理解,这里再出一个习题:“一个50μF的电容,在它的两端加上50V电压后,两极板上所带电量为多少?当它的两端电压加倍时,该电容器的电容为多少?”不妨依照电容的概念和公式自己算一算(答案为2.5×10\(^{-}\)3C和50μF)。
电子技术中的概念与公式不计其数,初学电子技术一定要掌握它的基本概念,在理解基本概念的基础上运用公式去解决问题。绝不能简单地找几个数字代代公式,得出不可靠的结论。正确的学习方法即是成功的一半。对于电子技术中的基本概念,明确了它的含义,理解了它的物理意义,一切问题也就迎刃而解了。 (谈小元)