电子技术是一门渗透性很强的学科,无论生产、科研、生活都离不开它。它能借助各种传感器把大自然中物理量、化学量的变化转换成电信号的变化,通过对这些电信号进行处理、加工、控制和传递,进而为人类服务。例如:电视技术就是先用摄像机将光和声音转变成电信号,经电视台加工后通过无线或有线的方式传送到千家万户,最后由电视机把电信号还原成光和声音。又如工厂流水线上的产品数量统计,产品每经过传感器一次,便产生一个电信号,最后对这些电信号进行统计处理就可以得出产品的生产数量。因此,掌握一些电信号的知识对学习电子技术是有帮助的。
自然界里能转变为电信号的物理量和化学量不计其数,如声、光、磁、力、温度、软硬、轻重、湿度、气体、浓度等等。如果我们对由各种物理量、化学量转变成的各种电信号进行分类,可分为规则电信号和非规则电信号,规则电信号又可分为周期电信号和非周期电信号,而周期电信号还可分为正弦电信号和非正弦电信号。假如按电信号在波形幅值上和时间上是否连续来分,又可分为模拟电信号和数字电信号两大类。下面我们分别对这两大类电信号加以分析。
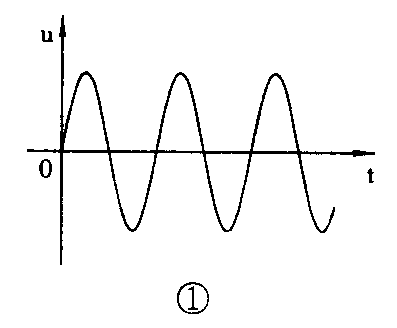
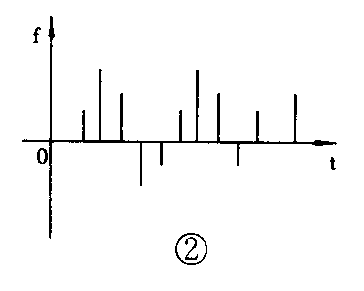
模拟电信号的特点是它的波形在幅值上一定是连续变化的,在时间上则可以是连续的,也可以是不连续的。例如声音经话筒转变成的电信号即为模拟信号。当声音传入话筒后,声波的机械振动引起话筒电场发生变化,从而产生了随声波变化而变化的交变电压。这种交变电压的波形尽管同声波一样很复杂。但它只是各种波形的合成物,在数学上用傅里叶级数分解法可以把它分解成许多个不同频率的正弦信号波。图1为其中的某一频率的波形。该信号电压在幅值上和时间上都是连续的,是一条没有间隙的连续曲线。从数学角度来讲,电压u是时间t的连续函数,意思是电压u的值和时间t是一一对应的,每一个时刻的t总有一个对应的电压u。图2为一幅度上是连续变化的而时间上是离散的信号波形,仍属于模拟电信号。研究分析模拟电信号只需掌握它的三个参数特性:周期(或频率)、振幅和相位。这三个参数在电工学上分析正弦交流电部分时讲述较多见,这里不再复述。
数字电信号是一些不连续的量,它不仅在幅值上是离散的,而且在时间上也是离散的。讲到数字电信号往往与脉冲信号分不开。在数字电路中需要的各类信号是用脉冲振荡器产生的或用已有的脉冲信号进行整形来获得。脉冲信号是指在短促时间内电压或电流突然变化的信号,从狭义来讲是指一种持续时间极短的电压或电流波形,从广义来讲,凡不具有连续正弦波形或正弦波高度失真了的波形,都属于脉冲波形。
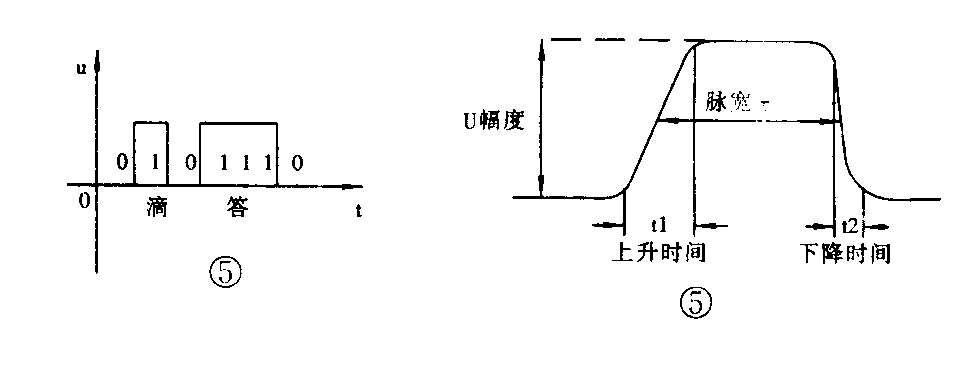
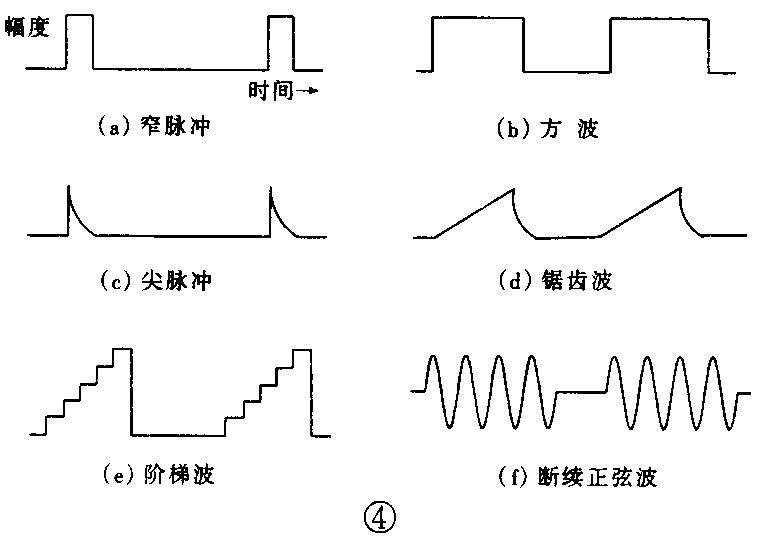
脉冲信号千变万化,种类很多,图3给出了常见几种脉冲信号的波形。从图中可以看出脉冲信号的特点为间断、突变。由于不连续,脉冲仅能用信号有、无或电平高低这两种状态来表示。因此人们通常用二进制数“0”和“1”来代表数字电信号的两种状态。例如在无线电等幅报通信时(CW),用电键发莫尔斯码中的“A”字(“滴答”)“答”的脉冲信号时间是“滴”的3倍,其电信号波形如图4所示,该信号用二进制数表示为10111。数字电信号应用最广的莫过于数字电子计算机,其内部全依靠数字电信号进行工作。由于二进制数的两个基本数码“0”和“l”,可用电子开关元件的“开”和“关”两种状态来表示,因此不管由“0”和“l”组成的二进制数像“天书”那样难读难记,在计算机里仅用电脉冲信号的“有”、“无”来表示即可,算法简单。另外,脉冲信号的频率可以做得很高,在1秒钟内可以产生几亿个电脉冲信号,用这种电脉冲来计数,难怪计算机的运算速度极快。
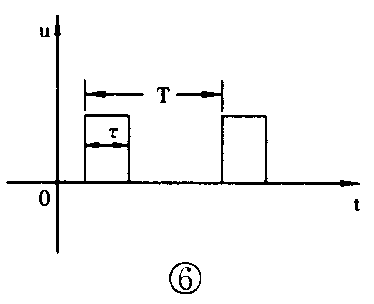
脉冲幅度U:表示脉冲电压或电流变化的最大值。
脉冲周期T:表示两个相邻脉冲重复出现的间隔时间。上升时间t1:脉冲从幅度的10%上升到幅度的90%所需要的时间,也称为脉冲的前沿宽度。下升时间t2:脉冲从幅度的90%下降到幅度的10%所需要的时间,也称为脉冲的后沿宽度。脉冲宽度τ(或称脉冲持续时间):指脉冲幅度的50%处的宽度。其值越大表示脉冲出现后持续的时间越长。
占空比:指脉冲宽度(脉冲持续时间)τ与脉冲重复周期T之比。占空比通常是小于1的数值。
近年来,在电子技术的新领域中,数字脉冲技术得到广泛应用。例如,日益普及的GSM移动通信系统就是采用数字通信方式。在家用电器方面,数码音响,激光音、视盘,也均采用数字电信号来工作,大有数字“取代”模拟之势。其实二者并不是孤立的,在电子技术应用中,常需要将模拟电信号和数字电信号进行相互转换,这就是通常所说的A/D或D/A转换。例如:用数字测量仪表测量一个模拟量,就必须先将模拟量变换为同频率的数字脉冲信号,然后才能用数字显示电路进行显示测量结果。又如用计算机进行自动控制,除了要求先把被控制的模拟信号转换为数字信号外(A/D转换),还得将计算机处理后的结果所得到的数字信号转换为模拟量(D/A转换),才能实现自动控制。此外,另有一些集成电路,既有模拟电路的功能又有数字电路的功能。如555时基电路是一种模拟——数字混合式集成电路,电路功能灵活,适用范围广,在自动控制方面有着广泛的应用。(谈小元)