通常我们将每倍频程衰减6dB(-dB/oct)的滤波器称为一阶滤波器。图1是最简单的一阶低通滤波器,它是无源滤波器。而每倍频程衰减12dB的滤波器称为二阶滤波器。通常的二阶滤波器以有源的居多。
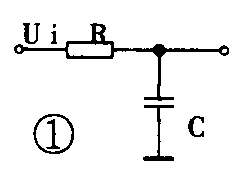
二阶滤波器的种类较多,有能提供最大平坦通带的Butterworth(巴特沃斯)滤波器。它有相当好的幅度与瞬态特性,使整个通带内和直流增益不一致的偏差最小。这种滤波器适合在仪表电路中应用,它的电路见图2中虚线右边部分。而Bessel(贝塞尔)滤波器则提供低的过冲和快速置定(即线性相位——平坦延迟)特性,它对所有频率等量延迟,保持阶跃输入形态,减轻对高频的衰减,比巴特沃斯滤波器稳定得快,适合从多路中选择一个信号送往模数变换器(A/D)的情况下使用。图2是一个四阶贝塞尔滤波器,虚线左边部分即为二阶贝塞尔滤波器。
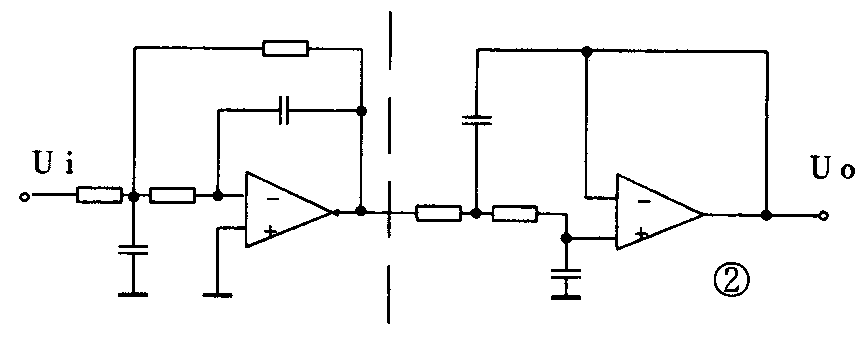
椭圆函数滤波器有最陡峭的频率倾斜缘,它那靠近边缘的高Q值极点结合阻带零点使衰减特性锐变,适合使用于要求阻带区锐减的场合。图3是一个三阶椭圆函数滤波器,虚线左边即为一个二阶有源低通椭圆函数滤波器,右边为一阶无源低通电路。该电路不仅电路复杂,而且计算步骤多。虽然有现成表格可查出数据进行计算,但算出的电容、电阻并非标称值,尤其是电容器可能要以一个以上并或串联达到计算值。而且须在电容电桥上测试挑选,否则元器件数值达不到一定的精度,除难以满足设计指标外,还可能引起电路自激振荡。
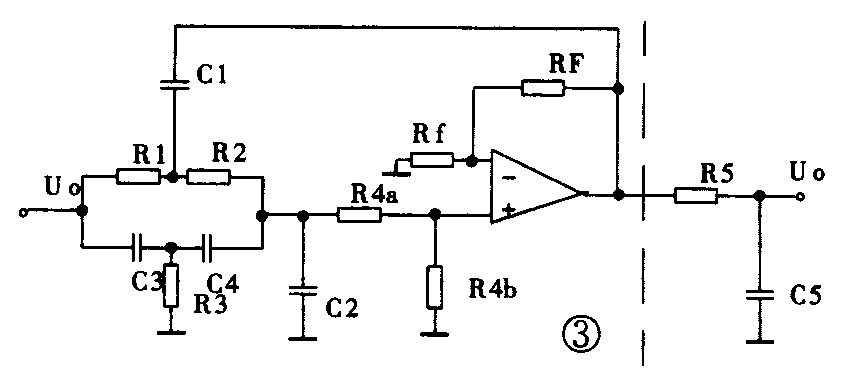
由美国MAXIM公司生产的MAX系列八阶低通滤波器集成电路,外形见图4(a)(b),它们是使用极为方便的模拟信号滤波器IC。这种IC几乎不用外接元件,可以单或双电源应用,只要选择适当的时钟频率送入该IC的CLK(时钟输入)端,即可达到滤波的目的。这种IC也可以使用内部振荡器,只需在CLK端对地接一个合适的电容器(见后计算)也可达到同样目的。IC内部有一个独立运算放大器,可与外接阻容元件构成用于后置滤波器或抗混叠的连续时间低通滤波器,以消除输出信号中产生的干扰。
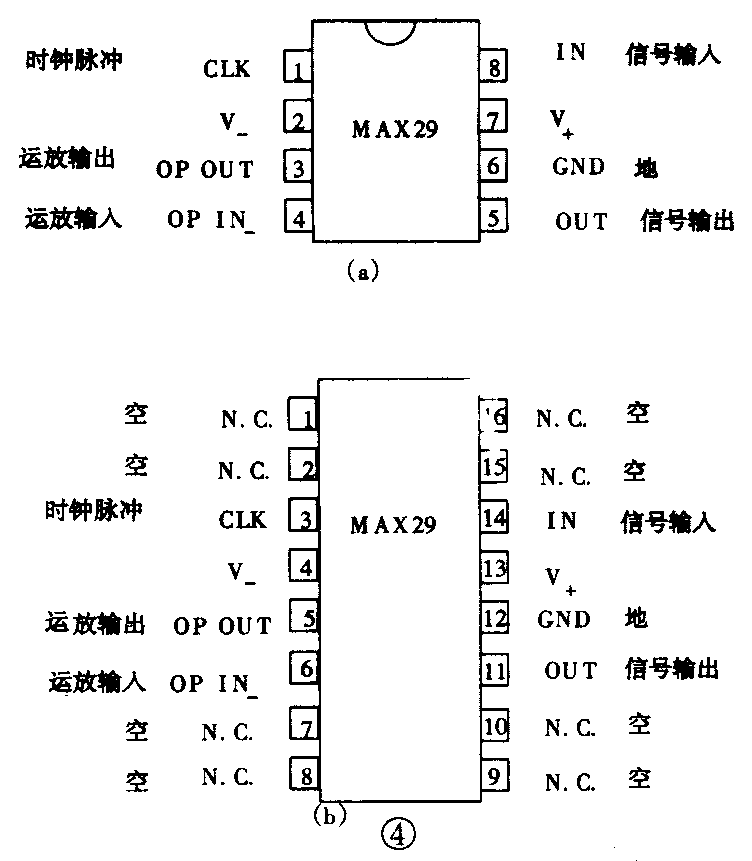
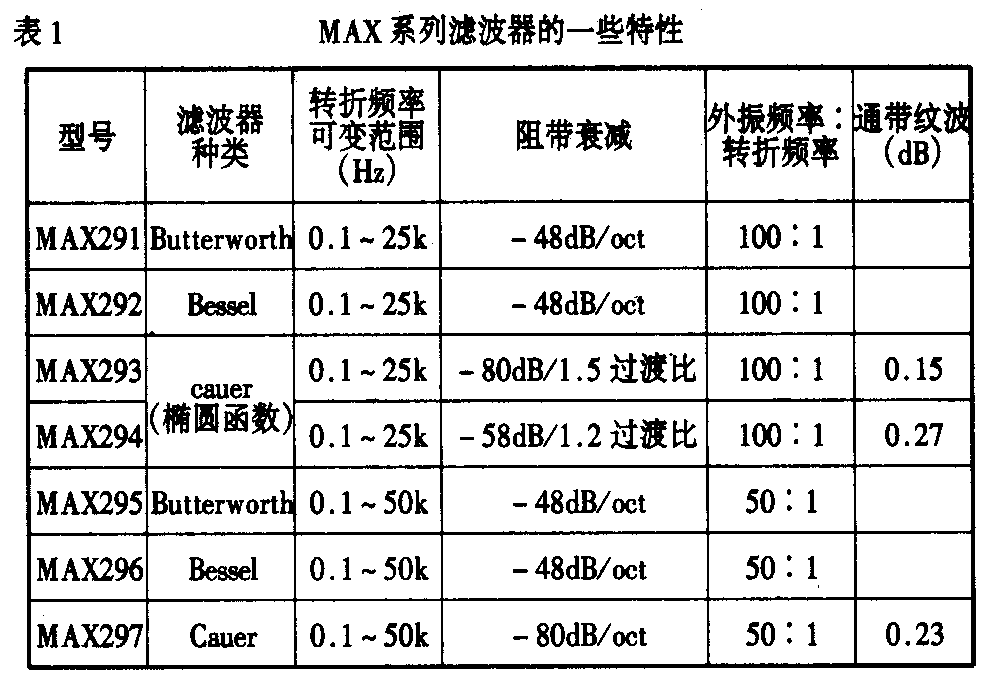
表1列出了MAX系列八阶滤波器的种类及特性,所谓“外接振荡频率:转折频率”,它指的是两种频率的比值。例如需要低通滤波器的转折频率是1kHz,而表2中给出的比值是100∶1,那么外接振荡器频率应该是100kHz。这些滤波器所允许的外接振荡器的最高频率为2.5MHz。
由图4看出,MAX系列滤波器的管脚排列有8脚与16脚两种封装形式。NC脚即空脚,CLK为时钟输入端,当用内部振荡器时,该脚对地端接一电容C,C=\(\frac{10}{^{5}}\)3f(pF)。式中f为所需滤波器的转折频率,如低通滤波器选择转折频率f=1kHz,则C=105;3×10\(^{3}\)=33pF\(_{o}\)V-与V\(_{+}\)分别是负、正电源端。GND是地端,在单电源使用时,它置于电源的中点上,IN与OUT分别是滤波器的输入、输出端。OP IN-与OP OUT则分别是内置独立运放的反相输入与运放输出端。
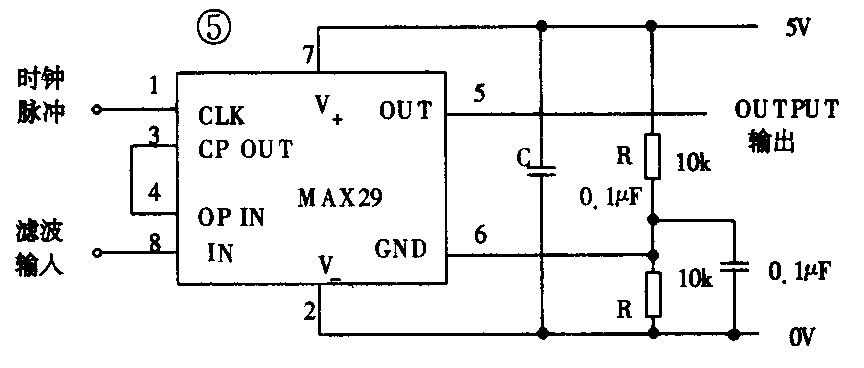
图5是该滤波器的典型运用,它使用了单电源,当内置运放不用时,将其反相端与输出端短接。C是电源退耦电容,R为分压电阻,使GND端接电源的中点。
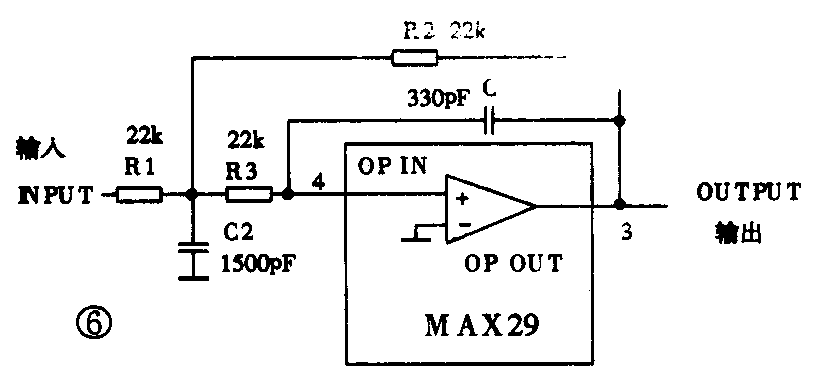
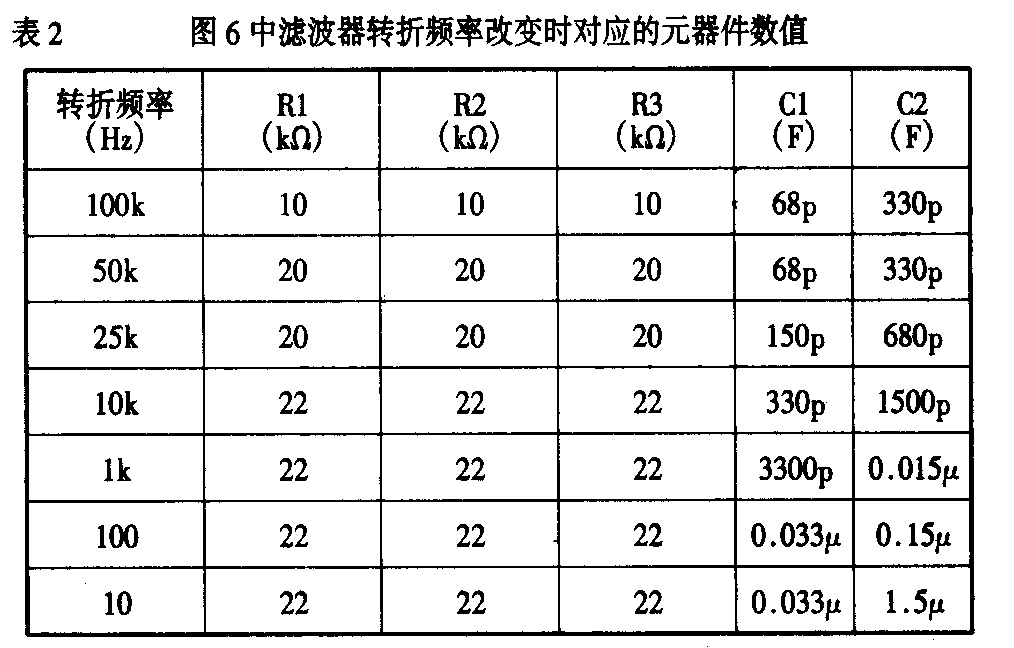
图6是独立运放所构成的低通滤波器。该运放的同相端已经在内部连接到GND端,这个独立运放构成的滤波器具有10kHz的转折频率,是二阶Butterworth滤波器,其输入阻抗大于22kΩ。表2给出了当这个滤波器转折频率改变时对应的阻容元件的数值。当选用椭圆函数滤波器时,这个独立运放所构成的滤波器的转折频率至少2.5倍于椭圆函数滤波器的转折频率,最好是5倍以上,以防止元件容差带来的通带误差。使用椭圆函数滤波器作D/A变换的后置滤波器时,要将D/A变换的时钟与滤波器的时钟同步,且D/A变换的时钟应该利用滤波器的时钟进行分频而取得,方能防止差频混进滤波器输出的通带内。(张国华)