电阻、感抗与阻抗,这些参数经常出现在电子技术的书刊中,但许多初学者对这几个参数的区别以及它们之间的关系搞不清楚,本文以扬声器的参数为例,来谈谈上述问题。
一只扬声器标明阻抗8Ω,若用万用表测量它的电阻为7.5Ω,阻值比所标阻抗值小,这是为什么?
我们知道扬声器是一种电声元件,它能把电信号转换成机械振动,通过空气传送声波到耳机使人们听到声音。因此,严格来说扬声器的阻抗不仅包括电阻抗还应包括机械阻抗、声阻抗。而一般扬声器所标明的阻抗主要是指电阻抗,就是指音圈的电阻抗。
音圈是用漆包线多层密排绕制而成的,它具有一定的电感量和铜线电阻,音圈的电阻抗就是由电感形成的感抗和铜线电阻合成的。那么音圈的阻抗与音圈的电阻以及感抗又有什么关系?这里我们先谈感抗。
感抗
我们可以做这样一个实验来了解电感的特性。用一个日光灯镇流器(15瓦至20瓦),电感量约10亨,铜线电阻约30Ω,一节一号干电池。用两只手分别捏住镇流器两根引线露出的铜线部分,同时去碰触电池的正负极,模拟一个瞬时变化的电流,你的双手会有什么感觉?!
当接触电池时,1.5伏电压加在镇流器和你的两只手上,电流由小增大,经过数秒钟达到稳定后,电流约等于1.5V/30Ω=50毫安。我们说镇流器储存了电流或电流产生了磁场。
当两手捏住镇流器的导线要撤离电池正负极时,电流要从50毫安减小,这时镇流器产生的自感电动势会阻碍50毫安电流使它不能立即减小,而是通过你的两只手缓慢地释放出来,在释放的开始一瞬间,自感电动势将达到50毫安乘上两手之间的人体电阻(就估算100kΩ吧)。你算一下这个电压值有多高?你必然会有所感觉。但因时间很短,对人体没有什么不良的影响。
通过这个实验使人们体验到自感电动势的客观存在。它存在的必要条件是电流是变化的。还可以体会到电感线圈储存电流的基本特性。自感电动势的产生和存储电流的特性使电感线圈具备了阻碍电流变化的作用,这就叫做感抗,用字母X\(_{L}\)表示。
显然,电流的大小变化得越快,频率f越高,阻碍作用也越大;自感系数L(电感量)越大,储存电流能力越强,阻碍作用就越明显。所以感抗X\(_{L}\)与频率f成正比,与电感量L也成正比。用数字定量表示它们的关系即:
X\(_{L}\)=2πfL=ωL
其中。ω=2πf是交变电流的角频率。
通过实验或理论计算都可以证明,交流电通过电感线圈时具有与直流电通过电阻时相似的关系形式,即
Im=Um/X\(_{L}\)或IRms=U\(_{Rms}\)/XL
其中Im、 Um是峰值,I\(_{Rms}\)、URms是有效值。
但是交流电的瞬时值i、U与X\(_{L}\)却不存在类似的关系。这是因为在电感电路中,电流瞬时值与电压瞬时值之间相位相差90°。也就是说最大值并不是同时出现的,它们之间相差\(\frac{1}{4}\)周期。电流总是落后电压1;4周期。用坐标曲线来表示这种关系见图1,从图上可以看出,电路接通的开始时刻,t=0时,交流电压u先达到最大值Um,而电流i是从0开始增长的。经过\(\frac{1}{4}\)周期,电流达到最大值时而不变化了。这时电压是0,如A点。又经过1;4周期,电流下降到B点为0,但是要改变方向,变化率是最大,它对应的电压U达到反向最大值。当电流由0反方向增长到达C点时又不变化了。所以C点对应的电压又从反向最大值下降到0。总之,电流与电压的最大值不是同时存在的而是相差\(\frac{1}{4}\)周期。如果用数学表达式写出来则:电流i=Imsinωt=I\(_{m}\)COS(ωt-90°),电压u=UmCOSωt
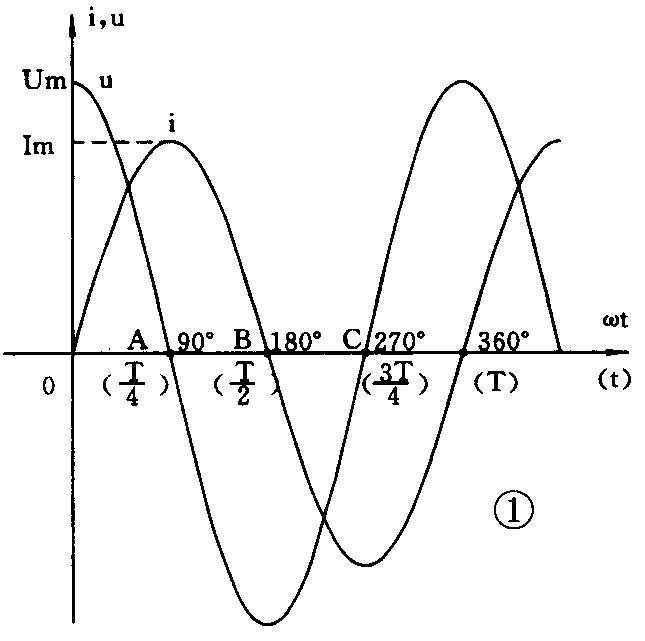
可以看出电流的相位落后电压的相位90°。因此,在同一时刻里,瞬时值u与i相除的关系不等于2πfL(X\(_{L}\)),而XL只是表示电压、电流最大值或有效值之间数值上的关系。从这里也看出X\(_{L}\)不是按正弦规律变化的,因此它也不是一个矢量。
阻抗
一个音圈的电阻抗,可以分解、简化成一个电感和一个电阻串联组成,如图2所示。在串联电路中。通过各元件的电流i相同。i=I\(_{ms}\)inωt=\(\sqrt{2}\)IRmssinωt,交流电流通过电阻时,在电阻上的电压与电流是同频率同相位的,都按正弦规律变化。所以i=U\(_{R}\)/R或IRms=U\(_{Rms}\)/R
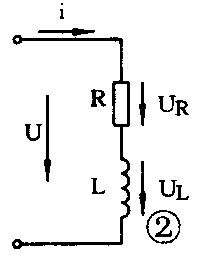
这个等式的形式与直流电路I=U/R相似。所以U\(_{R}\)=iR=IRm
Rsinωt=\(\sqrt{2}\)I\(_{Rms}\)Rsinωt=2URmssinωt=U\(_{Rm}\)sinωt
交流电通过电感时,电感上的电压U\(_{L}\)是超前电流i90°的同频正弦量
U\(_{L}\)=ULmsin(ωt+90°)=I\(_{Lm}\)XLsin(ωt+90°)=\(\sqrt{2}\)I\(_{Lrms}\)XLsin(ωt+90°)
=\(\sqrt{2}\)U\(_{Lrms}\)sin(ωt+90°)
按照电路理论电路两端总电压的瞬时值等于这两个分电压U\(_{R}\)与UL瞬时值之和,即U=U\(_{R}\)+UL=\(\sqrt{2}\)U\(_{Rms}\)sinωt+2ULRmssin(ωt+90°)
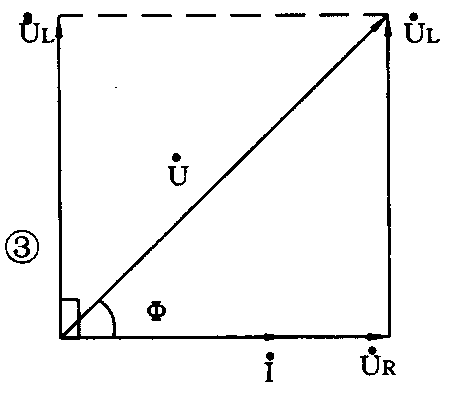
由于这两个瞬时值的相位相差90°。相加时用三角函数计算比较复杂,我们采用有效值矢量图来表示比较方便。那么总电压的有效矢量U·=U·\(_{R}\)+U·L,因为串联电路各部分的电流相同。所以用电流有效值矢量I·作为有效值矢量的参考轴,如图3所示。图中U·\(_{R}\)与I·同相,长度为I·R,U·L超前I·90°,长度为IX\(_{L}\)。U·、U·R、U·\(_{L}\)三个矢量构成了电压直角三角形,它的斜边表示总电压矢量U·,而U·L与U·\(_{R}\)互相垂直。因此总电压有效值的大小U=\(\sqrt{U}\)R\(^{2}\)+U\(_{L}\)2=IR\(^{2}\)+XL2,即直角三角形斜边的长度。这样,我们把\(\sqrt{R}\)\(^{2}\)+X\(_{L}\)2叫做电阻与电感串联后形成的阻抗,用符号Z表示。它的单位也是欧姆。具有阻碍电流通过的性质。它的大小由电路的参数R、L和信号频率f确定,而与电压电流的大小无关。由Z=R\(^{2}\)+XL2看出阻抗Z与电阻R、感抗X\(_{L}\)也构成一个直角三角形称XL是直角边,Z是斜边。它们之间的关系不是简单的相加,但也不是矢量。所以三角形各边不带箭头方向,仅仅表示三者之间数量上的关系。与电压三角形成相似三角形。因此也可以通过阻抗三角形求出电压之间的相位关系,如图4所示。
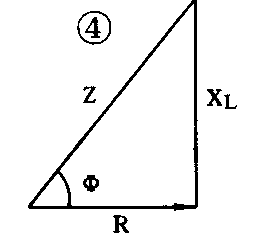
综上所述,一个音圈的阻抗Z是由铜线电阻R和音圈的电感X\(_{L}\)两部分构成的。如果音圈阻抗是8Ω,电阻是7.5Ω,通过1000Hz信号,可以算出感抗应当是2.78Ω。(王昌辉)