选购电源变压器时,常因吃不准其具体使用性能而犹豫。因为只测量空载输出电压并不能保证加负荷应用时也能符合要求。事实上任何变压器的有载输出电压都要比空载输出电压低一些甚至低许多。例如一些专为配合某种高档电子琴使用的12V电源适配器,其空载输出竟达17V之高,但在接入专用的电子琴之后却接近12V。
那么如何才能在商店售货台上就能对要购的变压器测判个八九不离十呢?下面介绍两种简单方法。
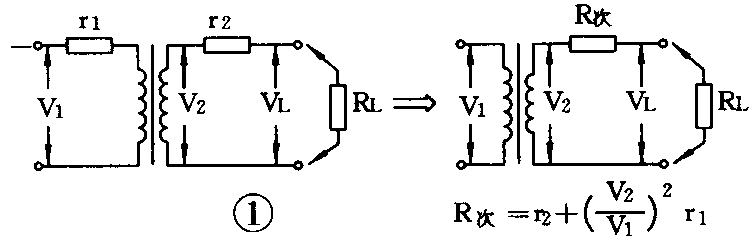
方法一:选定了要求的初、次级电压标称值后,用万用表的电阻测量档分别测出初、次级的直流电阻r\(_{1}\)和r2。由图1的等效电路我们可以把初级电路的电阻全部折算到次级去。这样,就得到了一个初级电阻为0,次级电阻为
R\(_{次}\)=r2+(V\(_{2}\)/V1)\(^{2}\)r\(_{1}\) (1)
的等效变压器电路。这个R\(_{次}\)正是引起次线有载时输出电压降低的原因。且负荷电阻越小输出电压就降得越低。据此可以导出一系列实用计算公式(证明从略):
负载为R\(_{L}\)时的实际输出电压
V\(_{L}\)=V2[RL/(R\(_{次}\)+RL)] ②
最大输出功率时的负载电阻应为R\(_{Lm}\)=R次 ③
最大输出功率P\(_{0}\)max=V2\(^{2}\)/4R\(_{次}\) ④
输出功率为最大值时的输出电压V\(_{0}\)max=V2/2 ⑤
要求提供电流为I\(_{0}\)时的实际输出电压
V\(_{0}\)=V2-I\(_{0}\)R次 ⑥
要求提供电压为V\(_{0}\)时的实际可供电流
I\(_{0}\)=(V2—V\(_{L}\))/R次 ⑦
以上各式中的V\(_{2}\)均为变压器的次级空载输出电压或变压器上标注的名义次级电压。
举例来说,若测得一变压器的初级电阻为r\(_{1}\)=100Ω,次级为r2=2Ω规;初级电压为V1=220V时次级空载输出电压为V\(_{2}\)=18V,试判断一下当要求该变压器能提供12V电压时的实际使用性能。
1.R\(_{次}\)=r2+(V\(_{1}\)/V2)\(^{2}\)×r\(_{1}\)=2+(18/220)2×100=2.67Ω
2.输出12V时
可提供的电流为
I\(_{0}\)=(V2-V\(_{L}\))/R次=(18-12)/2.67≈2.25A
可供使用的功率为
P\(_{0}\)=VL×I\(_{0}\)=12×2.25=27W
3.能提供的最大功率为
P\(_{0}\)max=V2\(^{2}\)/4R\(_{次}\)=182/(4×2.67)≈30W
4.能给出30W输出时的最佳负载为
R\(_{L}\)=R次=2.67Ω
5.能输出最大功率时的输出电压为
V\(_{Pm}\)=V2/2=18/2=9V
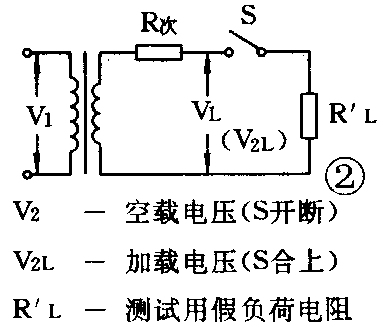
方法二:准备一只10~15Ω瓦数足够大的假负荷电阻R\(_{L}\)'(例如10Ω/5W的),用电压档测量变压器次级的空载和有载输出电压V2及V\(_{2L}\)。由图2的等效电路可以推知次级等效电阻为
R\(_{次}\)=R'L(V\(_{2L}\)/Ve-1) ⑧
然后就可以按照方法一的程序计算该变压器的实用性能,看是否适于你预期的目的。
例如,若一变压器,其次级输出电压的空载值为V\(_{2}\)=15V,接上10Ω负载时变为V2L=11V,则其内阻R\(_{次}\)=RL(V\(_{2}\)/V2L—1)=10(15/11—1)=3.64Ω
问:该变压器用于提供9V、3A的场合能否胜任?
利用公式⑦可求得输出9V时能供出的电流为:
I\(_{0}\)=(V2-V\(_{L}\))/R次=(15-9)/3.64≈1.65A(<3A),可见不能胜任3A电流的要求。利用公式⑥可求得供出3A电流时能输出的电压为:V\(_{0}\)=V2-I\(_{0}\)R次=15-3×3.64≈4.1V,可见满足了电流时又满足不了9V电压的要求。
最后,还应核算一下变压器铁芯能够承担的功率:
P=S\(^{2}\)/1.56 ⑨
式中S为铁芯中柱截面积(单位为平方厘米)。例如一变压器,其标签称“50W”,量得其芯柱尺寸为3×2.4cm\(^{2}\)(即变压器舌宽与叠厚的乘积),此厂家所示指标可信否?
用公式⑧可以算得P=S\(^{2}\)/1.56=(3×2.4)2/1.56≈33.2W。可见不应相信其“50W”之标签值。
验算满意后如有条件最好能再试两项实际性能:一是空载升温速率,二是额定功率输出时的升温速率。这两项指标关系到变压器的效率高低。通常,空载试验时,半小时的升温应基本无觉察;额定负荷时的最高升温不应引起手指的警觉感,仅应微温而已。(师业)