数字电路中常常需要各种各样的脉冲,它们通常是由脉冲振荡器产生的。此外,为了对脉冲信号进行整形、延时等加工的需要,还广泛使用着单稳触发器。脉冲振荡器和单稳触发器都是数字电路中的重要部件,它们都可以用门电路组成。
微分电路和积分电路
从电路的基本知识知道,由电阻和电容组成的分压电路,因连接方法和时间常数的不同可以分成微分电路和积分电路两种。
假定RC电路的时间常数是τ=RC,输入脉冲的宽度是t\(_{k}\)。那么,按图1(a)的接法并满足τ《tk条件时,就是一个微分电路。当微分电路输入端加上一个正脉冲时,在脉冲的上升沿,输入信号突然从低电平变到高电平时,输入电压对电容C充电,充电电流极大,充电电流在电阻R上的电压降是上正下负。由于电路的τ很小,充电电流很快减至零,所以输出端得到一个尖的正脉冲。在输入脉冲的下降沿,输入信号从高电平突然变到低电平时,电容C上已充满的电荷要放电,放电电流的方向是从下通过电阻R回到电容的另一端,所以输出端得到一个尖的负脉冲。两个尖脉冲形状相同,时间间隔是t\(_{k}\)。通过分析可以知道,微分电路的输出波形只反映输入脉冲的突变部分。即只有当输入脉冲发生正跳变或负跳变时才有输出,如果输入脉冲电压不变就没有输出。因为这个电路的输出电压Uo和输入电压U\(_{i}\)之间是近似的微分关系,所以称为微分电路。
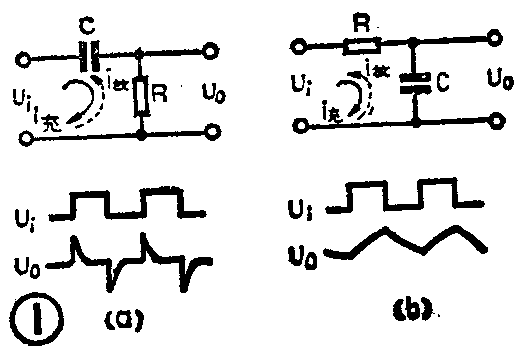
如果把R和C的位置互换,按图1(b)连接并满足τ》t\(_{k}\)的条件时,电路就成为一个积分电路。当积分电路的输入端加上正脉冲时,在输入电压突然从低变高时,电容开始充电,电容两端电压Uo=U\(_{c}\)按指数规律增长。由于τ很大,充电很慢。在输入电压突然从高变低时,充电过程还没有结束,电容C要通过电阻R放电,输出电压Uo逐渐下降。因此对应于输入端的正脉冲,输出电压的波形近似于一个三角波。因为这个电路的输出电压U\(_{o}\)和输入电压Ui之间是近似的积分关系,所以称为积分电路。
单稳态触发器
数字电路中除了大量使用双稳态触发器,还使用一种叫做单稳态触发器的电路。单稳态触发器的特点是:它有一个稳定状态和一个暂稳状态,在没有外来触发脉冲作用时它总是保持在稳定状态。在外来触发脉冲作用下,电路会从稳定状态翻转到暂稳状态;经过短暂的一段时间后,电路又会自动恢复到原来的稳定状态。因此,单稳触发器好象是一扇弹簧门,如果没有人推它,就一直保持关闭的状态。当有人推动它之后,它就会打开,但在开了一会儿后,它又自动恢复到关闭的状态。单稳触发器的暂稳状态的时间长短是由电路中RC元件的参数决定的,和触发脉冲没有关系。或者说,触发脉冲在这里只是起一种推动或开关的作用。
单稳触发器从工作原理上可以分成微分型单稳和积分型单稳两种。
(1)微分型单稳触发器
用两个与非门交叉连接,门1到门2用微分电路耦合,门2到门1用直接耦合,输入的触发脉冲加到门1的另一个输入端,便得到一个微分型单稳态触发器,如图2(a)。有时为了突出输入输出的关系,也可画成图2(b)。
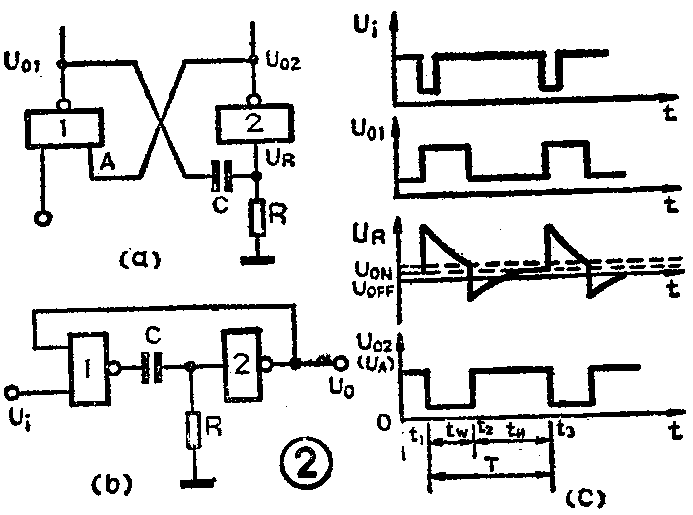
微分型单稳电路规定在没有触发脉冲时输入电压U\(_{i}\)是高电平,这时输出电压U02也是高电平,这个高电平输出就是微分型单稳电路的稳态。它交叉耦合到门1的输入,使门1的输出U\(_{0}\)1为低电平。在没有触发脉冲输入时各点电压的波形见图2(c)中0~t1所示。
微分型单稳电路是用负脉冲触发的。假定电路在t\(_{1}\)时刻,输入一个触发脉冲,即Ui突然由高变低,则U\(_{0}\)1应从低变高,UR随之突变为高电平,U\(_{0}\)2随之变成低电平。U02同时耦合到门1的输入端使U\(_{0}\)1维持为高电平。这是暂稳态的开始,见波形图中t1点。暂稳态开始后,随着电容C的充电,U\(_{R}\)逐渐下降,当下降到等于门2的关门电平UOFF时,门2又重新截止,U\(_{0}\)2恢复为高电平。从暂稳态开始到输出又翻转成高电平的全部时间就是暂稳态时间tW,如波形图中t\(_{1}\)~t2所示。暂稳态结束后进入恢复阶段,这时U\(_{0}\)2的高电平送到门1的输入端A,门1的另一个输入端上的触发脉冲早已消失,也已恢复了原来的高电平,因此门1的输出U01成为低电平。由于U\(_{0}\)1降到低电平,电容C要放电,在电阻R上形成负电压。随着放电电流的减少,UR逐渐上升,到放电基本结束时才恢复原来的U\(_{R}\)值。从波形图看到,t2~t\(_{3}\)正是单稳触发电路的恢复阶段。根据计算,暂稳时间约为:tW=(0.7~1.3)RC;恢复时间约为:t\(_{H}\)=(3~5)RC。如果在单稳触发电路恢复稳态以后又有触发脉冲输入,电路就会重复以上的过程,因此从输出端得到的将是一串脉冲宽度不变的脉冲。而这串脉冲的脉冲宽度实际上就是暂稳时间tW。因为t\(_{W}\)只和R、C的数值有关,所以通过调整R、C的数值可以得到不同脉冲宽度的脉冲串。
(2)积分型单稳触发器
如果两个门之间用积分电路耦合,并且使输入触发脉冲同时加到两个门的输入端,如图3(a),便得到一个积分型单稳态触发器。有时按输入输出的顺序可以画成图3(b)。
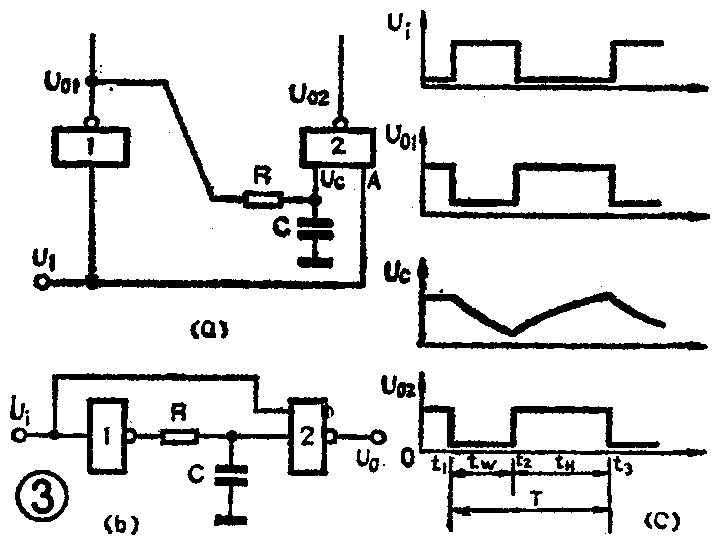
积分型单稳电路规定在没有触发脉冲时输入电压U\(_{i}\)是低电平,这时U01和U\(_{0}\)2以及电容C上的Uc都是高电平,见图3(c)中0~t\(_{1}\)时各点电压波形。因此积分型单稳电路的稳态是高电平。
积分型单稳电路是用正脉冲触发的。假定在t\(_{1}\)时刻,输入一个触发脉冲,即Ui突然从低变高,则U\(_{0}\)1应从高变低,门2的输入A已经是高电平,另一个输入是从U01经过积分电路送来的,因为电容上的电压不能突变,所以U\(_{c}\)一开始仍维持为高电平,然后逐渐下降。于是门2的输出U02变成低电平,这是暂稳态的开始,见波形图中t\(_{1}\)点。暂稳态开始后,随着电容C的微电,Uc逐渐下降,当U\(_{c}\)下降到等于门2的关门电平UOFF时,门2又翻转,恢复到原来的高电平,暂稳态结束。波形图中t\(_{1}\)~t2这段时间就是电路的暂稳时间t\(_{W}\)。和微分型单稳电路相同,积分型单稳电路也有一个恢复阶段。在恢复阶段,U01对电容C充电,U\(_{c}\)逐渐上升到原来的高电平时,恢复过程结束,见波形图中t2~t\(_{3}\)时的波形。根据计算,积分型单稳电路的暂稳时间约为;tW=1.1RC;恢复时间约为:t\(_{H}\)=(3~5)RC。如果在电路恢复稳态以后又加上触发脉冲,电路就会重复以上过程。从输出端得到一串脉冲,脉冲宽度就是tW。
单稳触发电路可以用来对脉冲波形整形或作定时、延时用。一个脉冲经过一段线路的传输之后,波形常常会发生变化,变得不规整甚至因干扰而带上毛刺。把这种失真了的脉冲送入单稳触发电路,从它的输出端可以得到和输入脉冲频率相同,脉宽和幅度都规整的方波。
数字系统中各个电路常常是严格地按时间先后有次序地工作的。例如有两个电路,要求第二个电路比第一个电路滞后一段时间工作,或者说作用在第二个电路上的触发脉冲应该比第一个电路上的错后一段时间,这就是延时的要求。这时只要用触发脉冲经过单稳触发电路以后再作用到第二个电路上,就可达到目的。延时的时间就是单稳触发电路的暂稳时间t\(_{W}\)。(未完待续)(俞鹤飞)