数字电路中使用的是数字信号,它们是一串串的电脉冲。这些脉冲的不同组合代表着各种信息:有时它代表数字:有时它表示文字符号;有时它只是告诉机器应该完成某种操作。也就是说,数字电路中的电脉冲实际上是“数字化”了的各种信息。
那么,数字电路中的数字有些什么特点呢?让我们先从数制谈起。
什么是二进制教
我们日常使用的是十进制数。它使用0、1、2、……9共十个数字符号,它的基数是十。它的计数方法是每计满十个数时要向高位进位,也就是“逢十进一”。
除了十进制数,我们还使用着其它进位计数制。例如十二进制数:一打铅笔12支,一年有12个月;十六进制数:我国的老秤是一斤有16两;六十进位制:一小时60分,一分60秒等。
数字电路中使用的是最简单的二进位计数制。二进制计数法只有0和1两个数字符号,它的基数是2。它的计数方法是每一位计满2就要向高位进位,也就是“逢二进一”。附表中的第2列表示出和十进制数对应的二进制数。
十进制数是按照高位到低位从左向右排列的。每个数字因所在的位置不同而有不同的位值。例如1989中有二个9,最有边的9在“个”位上,它的值是9;在它左边的9在“百”位上,它的值是900。整个数字的值是一千九百八十九。也可以写成:
1989=1×10\(^{3}\)+9×102+8×10\(^{1}\)+9×100
其中,10\(^{3}\)、102、10\(^{1}\)、1O0就是每一位的位值,我们把它叫做十进制数每位的“权”。每一位的数码乘上该位的权就是这位数的大小。上例中,右边的9的权是10\(^{0}\),所以它的数是9×100=9;而在它在边的9的权是10\(^{2}\),所以它的数是9×102=900。
二进制数也是按高位到低位从左向右排列的。但因为它的基数是2,所以它每位的权是以2的几次方变化的。例如二进制数1011100各位的权可表示如下:
1 0 1 1 1 0 0
2\(^{6}\) 25 2\(^{4}\) 23 2\(^{2}\) 21 2\(^{0}\)
这个二进制数相当于十进制数的值是:
(1011100)\(_{2}\)=1×2\(^{6}\)+0×25+1×2\(^{4}\)+1×23+1×2\(^{2}\)+0×21+0×2\(^{0}\)
=64+16+8+4
=(92)\(_{1}\)0
为了区别,我们在十进制数外面加()\(_{1}\)0表示或者在后面加一个缩写字母D;在二进制数外面加()2或在后面加字母B表示。
数字电路中为什么用二进制
计算机和自动控制设备中使用的都是数字电路。计算机的主要工作是计算,而自动控制设备中也常常有数值计算的要求,因此选用什么数制是和整个设备的工作效率有关的。
首先,从电路上能否实现来考虑。如果使用十进制,就要求电路中有对应的十种状态,这将使电路变得非常复杂,实际上很难实现。如果改用二进制只需要有和0、1相对应的两种状态。而这两种状态在电路中是很容易实现的,如开关的“开”和“关”,灯的“亮”和“灭”,脉冲的“有”和“无”,电平的“高”和“低”等等。
其次,从运算规则上考虑。十进制数的加法和乘法运算都很复杂,各有55条“九九口诀”。按照这样的运算规则设计出来的电路一定是很复杂的,运算的速度也快不了。
二进制的加法规则是最简单的,只有四条:
0+0=0
0+1=1
1+0=1
1+1=10
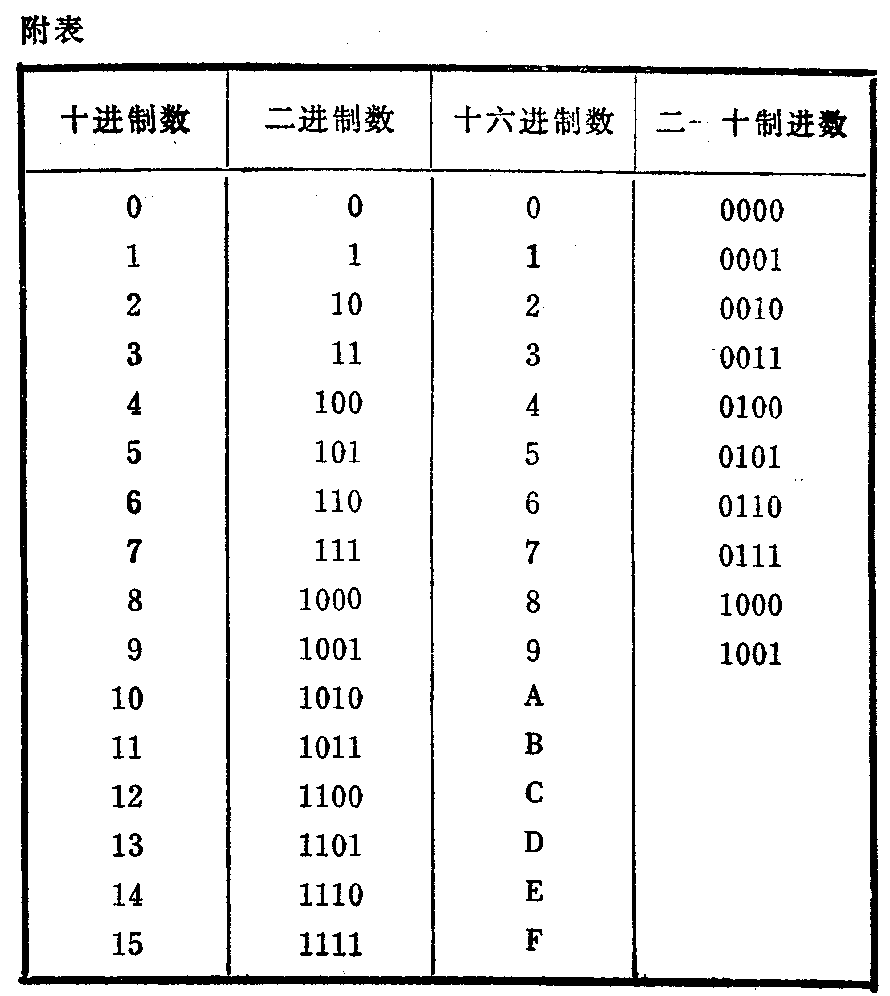
第4条是因为二个1相加产生进位而成为10。例如用二进制加法做十进制数6+5时,运算过程非常简单:
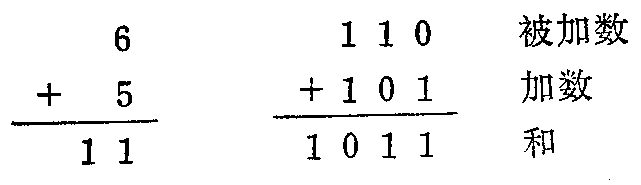
二进制的乘法规则也很简单,也只有四条:
0×0=0
0×1=0
1×0=0
1×1=1
例如用二进制乘法做个进制数6×5的过程是:
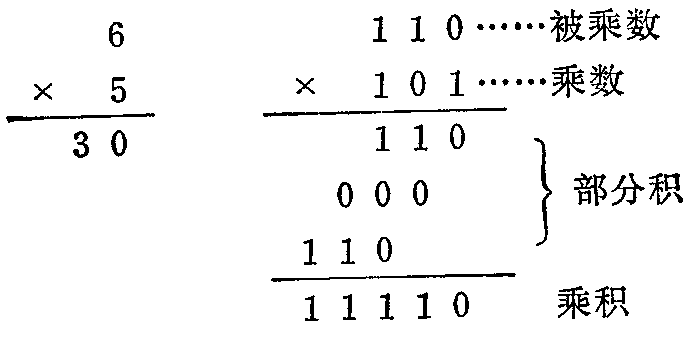
从乘法过程看到:乘数是0时,部分积是000;乘数是1时,只要被乘数110全部写下来就成为部分积,不过为了把位对齐,要把被乘数相应地向左移。当乘数各位部乘过以后,把所有的部分积总加起来就得到乘积。可见二进制的乘法可以通过移位的办法用加法来完成。也就是说,数字电路中只要用一个加法器再配上其它辅助电路就可以完成全部四则运算。
目前,数序电路的运算速度一般是一秒钟内能做几万或几十万次加法,大型计算机则已经快到每秒几亿次。电脑的运算速度远远超过了人脑!能够达到这样高的运算速度,集成化技术和脉冲技术的发展是一个原因。另一方面,采用二进制计数方法,运算规则特别简单,也是一个重要原因。
最后从设计方面考虑,由于二进制数只有0和1两个符号,可以利用逻辑代数把电路设计问题变成数学问题,加快了设计速度,提高了电路质量。
二进制数也有缺点,就是它的位数很长,不好读不好记。为了帮助阅读和记忆,我们常常把二进制数改写成十六进制数,使位数缩短,就好读好记了。十六进制数的基数是16,使用0~9和A、B、C、D、E、F共16个符号。见表1的第3列。它的表示方法是在数字后面加缩写字母H。由于一个十六进制数相当于四位二进制数,因此一个较长的二进制数改用十六进制数表示后就变得可读可记了。例如
(10001010)\(_{2}\)=(8A)16=8AH
(01000001)\(_{2}\)=(41)16=41H
二进制数和十进制数的转换
(1)十进制数转换成二进制数
十进制整数转换成二进制数时用“除2取余”法。把一个十进制整数连续除以2,把每次得到的余数从后向前排列就是二进制数。
例:(35)\(_{1}\)0=(100011)2转换过程如下:

(2)二进制数转换成十进制数
二进制数转换成十进制数时用“按权相加”法。把每位二进制的权值相加起来就是十进制数。在数制中,规定整数从低位到高位的排列次序中,把第1位称为第0位。因此,二进制数各位的权值如下:
B\(_{9}\) B8 B\(_{7}\) B6 B\(_{5}\) B4 B\(_{3}\) B2 B\(_{1}\) B0
2\(^{9}\) 28 2\(^{7}\) 26 2\(^{5}\) 24 2\(^{3}\) 22 2\(^{1}\) 20
512 256 128 64 32 16 8 4 2 1
例:(101001)\(_{2}\)=1×2\(^{5}\)+O×24+1×2\(^{3}\)+0×22+O×2\(^{1}\)+1×20
=32+8+1
=(41)\(_{1}\)0
二——十进制码
数字电路中,把0和1两种符号的组合统称为代码,意思是“代表某种信息的码”。
最简单的代码是二进制码。一个二进制数例如1100011,在数字电路里它表示是一串脉冲,我们就把它叫做二进制代码或二进制码。或者反过来说,这串代码现在是表示一个二进制数。除了二进制代码以外,用0和1的组合还可以表示十进制数、英文字母或汉字字符、某种操作等,它们分别被称为十进制码、字符码、操作码等。
当我们需要向数字电路输入十进制数时,首先遇到的一个问题是用什么方法表示十进制数?十进制数有0~9十个符号,要求有相应的十种状态。而数字电路中只有0和l两种状态,因此只能用0和1两个符号组合成的一组代码来表示十进制数。二位二进制数可以有4种组合,三位二进制数有8种组合,四位二进制数有16种组合。所以要想用二进制码表示一位十进制数至少要用四位二进制数。这种用四位二进制数表示一位十进制数的代码就叫做“二进制形式编码的十进制数”,简称二——十进制码或BCD码。
BCD码的表示形式是以四位二进制数为一组,它是在二进制数的基础上,把原来二进制数前面的空位补上0凑齐四位而组成的。例如十进制数0表示为0000,1表示为0001……。见表1的第四列。因此,一个十进制数1989写成BCD码就是:
(1989)\(_{1}\)0=(0001100110001001)2-10
由于这种BCD码从高到低各位的权分别是8、4、2、l,所以又称为8421码。
除了数字代码,数字电路中还使用着大量的字符代码。例如可以输入英文字母、数字和符号的国际标准码,或简称ASCII码。它用七位二进制码表示一个字母、数字或符号。例如:
字母‘A’=(01000001)\(_{2}\)=41H
数字‘9’=(00111001)\(_{2}\)=39H
加号‘+’=(00101011)\(_{2}\)=2BH
最后,要指出的是:BCD码虽然在形式上是二进制,但它并不是真正的二进制数,它必须变换成二进制数以后,才能工作。
复习思考题
1.数制转换练习
①(37)\(_{1}\)0=()2=()\(_{2-1}\)0
②(138)\(_{1}\)0=()2=( )\(_{2}\)-10
③(1010101)\(_{2}\)=()10=()\(_{2-1}\)0
④(1111111)\(_{2}\)=()10=()\(_{2-1}\)0
⑤(000101010011)\(_{2-1}\)0=()10=()\(_{2}\)
上期思考题答案
2.TTL与非门输入端悬空,也就是多发射极管T\(_{1}\)的发射极开路。悬空的发射极不可能有电流通过,从逻辑效果上看和接高电平是等效的。(俞鹤飞)