(俞鹤飞)数字电路的设计,通常是从给出的逻辑要求开始,先画出真值表,再从真值表写出逻辑表达式,然后从逻辑表达式画出逻辑电路图。但是从真值表直接得到的逻辑表达式在实用上并不一定是最合理的,常常要进行化简或变换以后才能得到最经济最合理的结果。另外,有时虽然逻辑电路图是合理的,但由于产品规格以及生产工艺的问题,也往往不得不对原有的电路进行一些修改或变换,使之切合实际。因此逻辑表达式的化简和变换是逻辑电路设计中一项极重要的工作。
逻辑表达式的化简和变换是利用逻辑代数中的一些基本公式进行的。那么,逻辑代数中有那些基本公式,它们又是怎样进行化简和变换的呢?
逻辑代数的基本公式
逻辑代数中有不少基本公式,它们有的和普通代数在形式上相似,有的则是普通代数中没有的。
其中和普通代数相似的公式有,
(1)交换律
A+B=B+A ①
A·B=B·A ②
(2)结合律
A+(B+C)=(A+B)+C ③
A·(B·C)=(A·B)·C ④
(3)分配律
A·(B+C)=AB+AC ⑤
以下的公式则是逻辑代数特有的:
(4)还原律(对合律)
A==A ⑥
(5)重叠律
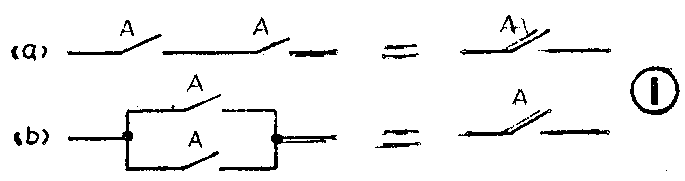
A+A=A ⑦
A·A=A ⑧
这两个公式画成开关电路如图1(a)和(b)所示,可以看到它们是成立的。
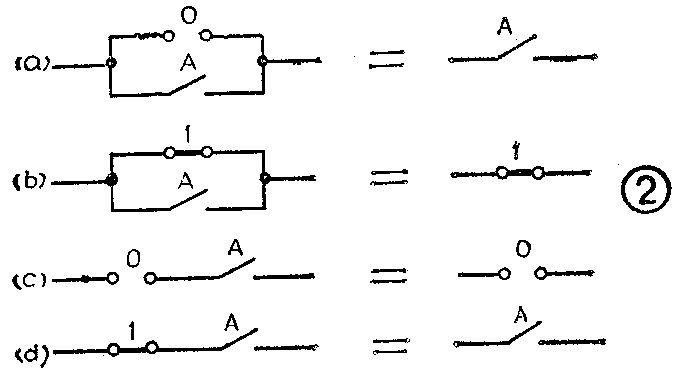
(6)0-1律
0+A=A ⑨
1+A=1 ⑩
0·A=0
1·A=A
它们对应的开关电路见图2。其中⑨、、三条和普通代数在形式上相似。第⑩条在对照图2(b)后也容易理解:一个常闭接点和接点A并联,接点A是不起作用的。
(7)互补律
A+A-=1
A·A-=0
它们对应的开关电路见图3。图中接点A和A-是在同一继电器上的一对接点,它们总是处于一开一合的状态,这种关系称为互补。从图看到,无论接点A为1或0,图3(a)总是接通的,图3(b)总是断开的。
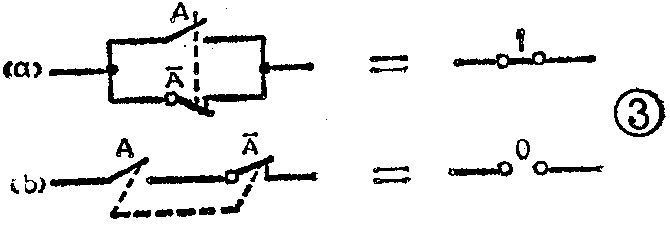
(8)吸收律
A+A·B=A
A·(A+B
对应的开关电路见图4。从图可见,不管接点B是什么状态,A=1时电路接通,A=0时电路断开,接点B实际上是不起作用的。
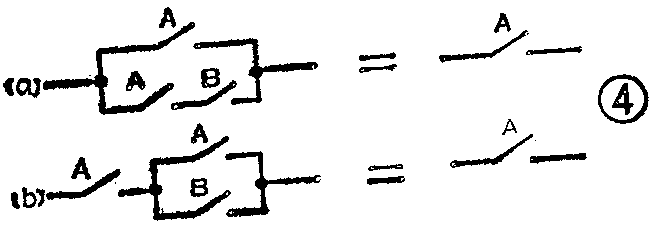
(9)消去律
A+A-B=A+B
A·(A-+B)=A·B
这两个公式可以用前面的公式来证明。
A+A-B=A+AB+A-B (吸收律)
=A+B(A+A-) (分配律)
=A+B (互补律)
A-)=AA- (分配律)
=0 (互补律)
=AB
(10)反演律(摩根定理)
A+B-=A--
A·B-=A--
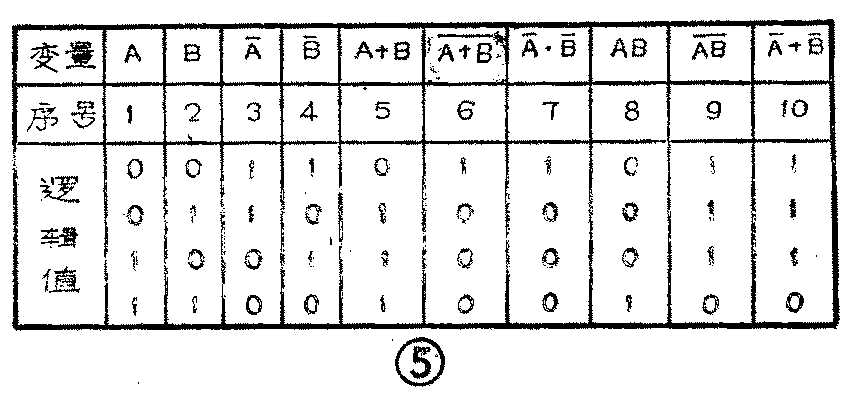
这是两条经常使用的公式,它说明“与”运算和“或”运算之间是可以互相转换的。把或运算变换成与运算;把与运算变换成或运算。如果把各个逻辑变量和运算的结果列成表,如图5那样,可以看到第6列和第7列相同,即证明了A+B-=A--;第9列和第10列相同,即证明了AB-=A--。
逻辑电路的化简
利用上面的基本公式进行合并、消去及变换等运算,可以使逻辑表达式变得更简单。最简逻辑表达式意味着得到的逻辑电路将是使用门电路最少、传输时间最短、最经济合理和最可靠。
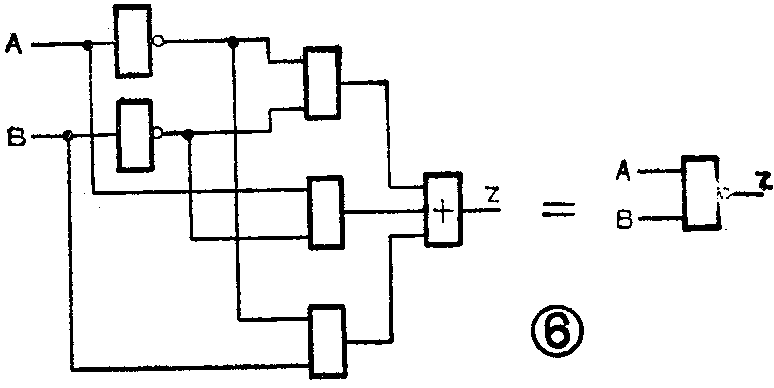
上一讲举出一例,从真值表得到的函数是Z=AB--B-,现在进行化简如下:
Z=AB-+A-B+AB-
=AB-+AB-+A-B+AB- (重叠律)
=A-(B+B-)+B-(A+A-) (分配律)
=A-- (互补律)
=AB-(摩根定律)
可见经过化简,逻辑表达式只有一项。原来要用二个非门三个与门一个或门的电路现在只用一个与非门如图6所示。
又如要求设计一个三输入变量表决逻辑电路。也就是在三个输入变量A、B、C当中,只要有两个或两个以上的变量是1时,输出变量Z为1。按照这个要求我们来进行设计:
第一步,按照逻辑功能要求列出真值表,如图7(a)。
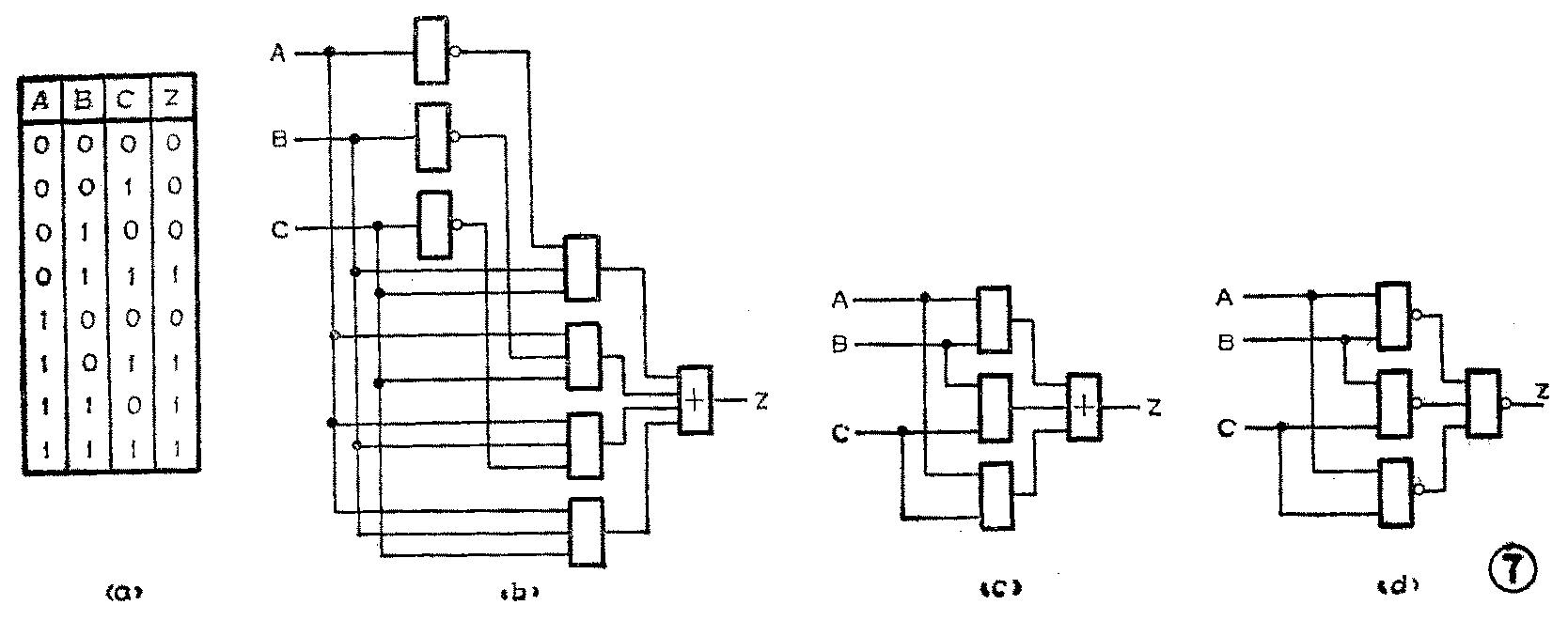
第二步,从真值表写出逻辑表达式。因为真值表中函数值Z等于1的共有四项,所以得到的逻辑表达式是:
Z=A-BC-C+ABC-+ABC
第三步,对逻辑表达式化简。从上面式子如画出逻辑电路图,如图7(b)。可见需要三个非门四个与门和一个或门。如把上式再进一步化简:
Z=A-BC-C+ABC-+ABC
=(A-BC+ABC)+-C+ABC)+(ABC-+ABC) (重叠律)
=BC(A+A-)+AC(B+B-)+AB(C+C-) (提公因子)
=AB+BC+AC
最后得到的式子只有三项,与它对应的逻辑电路图只要三个与门一个或门,见图7(c)。从节约的观点看,化简后的电路比原来的电路少用四个门电路。从传输质量看,原来的电路信号从输入到输出要经过非门、与门、或门三级传输,现在则只要二级,因此信号传输的时间缩短,对高速电路来说,传输质量提高了。
逻辑电路的变换
有时即使我们得到了最简的逻辑表达式,却不一定符合生产实际。例如数字集成电路是现代化生产,生产批量越大成本越低。因此生产厂家往往是减少品种,大量生产通用的品种。例如与非门就是最通用、生产量最大的,所以设计好了的电路常常希望能再进行变换,多使用与非门。
例如前面介绍的三变量表决电路用了三个与门和一个或门。还可以继续变换使电路只使用与非门一种元件:
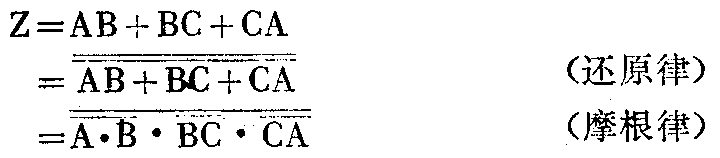
电路可用四个与非门实现,如图7(d)。显然,这个电路是经济合理和切合实际的,因为使用的元件从二种减到一种,而且是最通用最低廉的与非门。
又如,假定要求设计一个两输入变量的电路,当两个输入变量相同时,输出变量为0;两个输入变量相异时,输出变量为1。
按照这个要求我们来进行设计。第一步,列出真值表,见图8(a)。
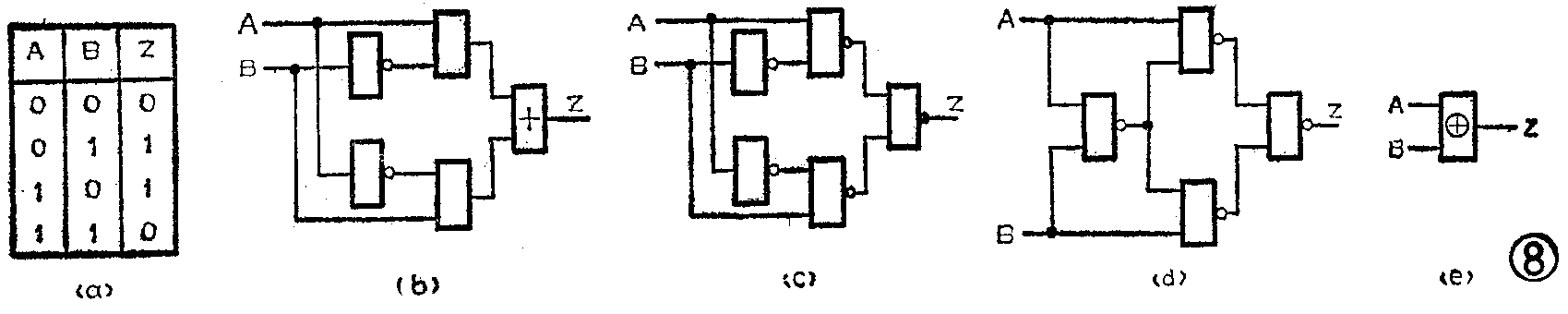
第二步,从真值表写出逻辑表达式:
Z=A-B-
第三步,化简和变换。按上式得到的电路要用两个非门两个与门一个或门,如图8(b)。因此还要进行变换才能得较为理想的电路。如按以下步骤变换:

如果非门也用与非门代用,则上式共使用五个与非门,如图8(c)。
如按以下步骤变换:
Z=A-B+AB-
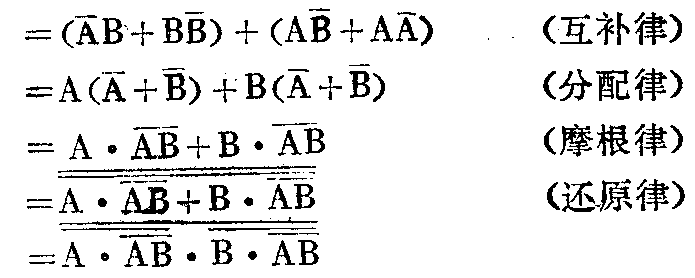
则只要四个与非门,如图8(d)。
由于这个电路在数控和计算机方面使用较多,是组成一种叫做加法器的部件的主要电路,因此集成电路专门成批生产具有这种逻辑功能的电路。这种电路有两个输入端、一个输出端,因为它具有“输入相异时出1”的特性,所以被称为“异或门”,并专门用一个特殊的逻辑符号来表示,见图8(e)。它的特殊的运算符是“,所以异或门的逻辑表达式一般写成
Z=A
通过以上的化简和变换,可以知道逻辑表达式不是唯一的,可以是多种多样的。利用公式进行化简和变换的方法常常是灵活多变的,并没有一定的模式。但化简的最终目的应该是:逻辑表达式中包含的项数最少,每个项中的变量最少。这样得到的电路便是输入变量最少、使用门电路最少、传输时间最短的电路。
复习思考题
1.逻辑代数中有那些基本公式?
2.化简下式
(a)Z=ABC-C+ABC--C-
(b)Z=A-B-
上期思考题答案
2.从或门的真值表得到的逻辑表达式是:
Z=A-B-