CMOS—LED显示组合器件

在数字控制系统以及各种数字仪表中，对数字信号的计数和显示多分别采用不同功能的多个单元电路，使用很不方便。本文向读者介绍两种目前应用较广泛的CMOS计数—锁存—译码驱动与LED数码显示器组合器件，它将上述五种功能集于一体，通常称为“五合一”电路。

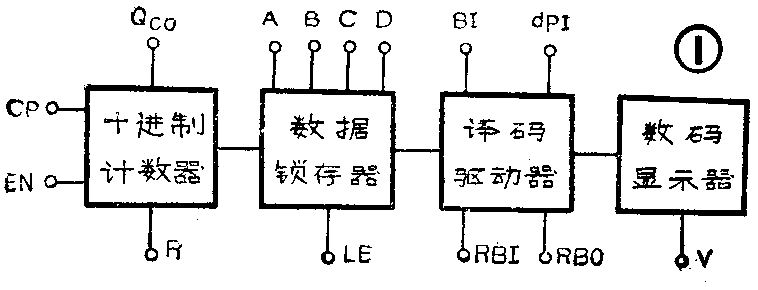
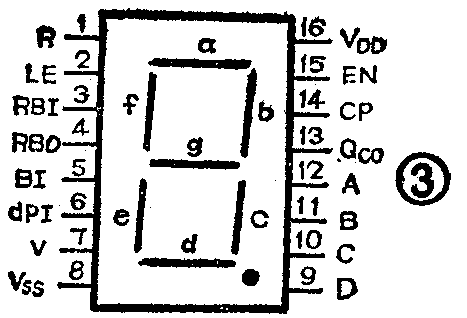
图1是CL102的逻辑框图，内部逻辑电路如图2所示。它由二—十进制计数器、四位数据锁存器、七段显示译码器及驱动器、LED数码显示器以及消隐电路构成。下面分别介绍各部分电路的工作原理。

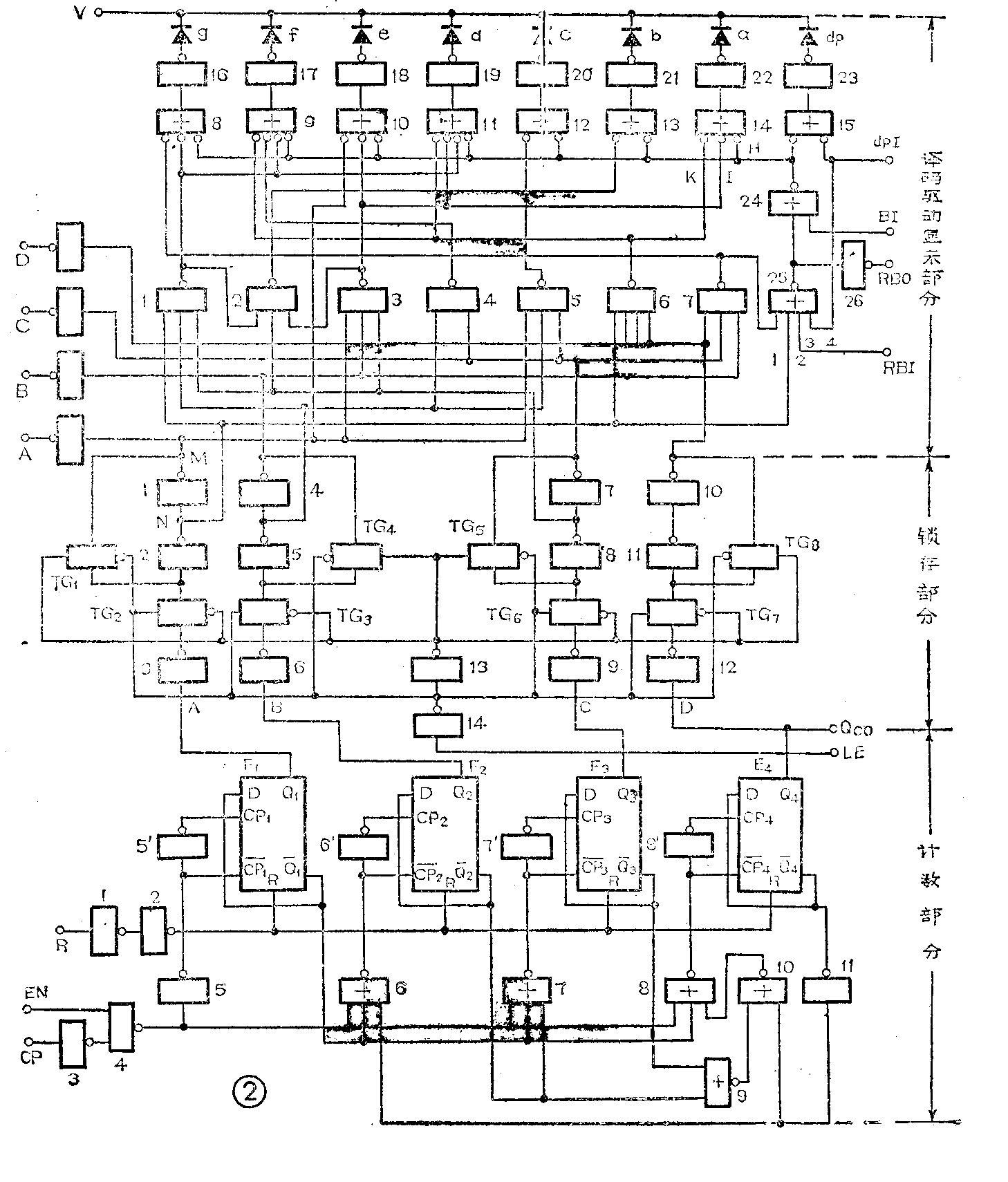
1．二—十进制计数器：图2中，D触发器F\(_{1}\)～F4以及门1～门11组成二—十进制同步计数电路。它有两个时钟输入端：CP和EN。如果要用时钟脉冲的上升沿触发，则脉冲由CP端输入，并将EN接高电平“1”；如果用时钟脉冲的下降沿触发，则脉冲由EN端输入，并将CP接低电平“0”。计数器的计数单元是由D触发器（D、Q-端相连）构成的T型触发器。T型触发器的逻辑功能是：从CP端每输入一个时钟脉冲，触发器状态就翻转一次，即：Qn\(_{+}\)1=Q-n。现假定计数器的初始状态为“0000”，若把时钟脉冲CP的作用也考虑进去，四个T型触发器（F1～F\(_{4}\)）控制端的控制方程分别为：

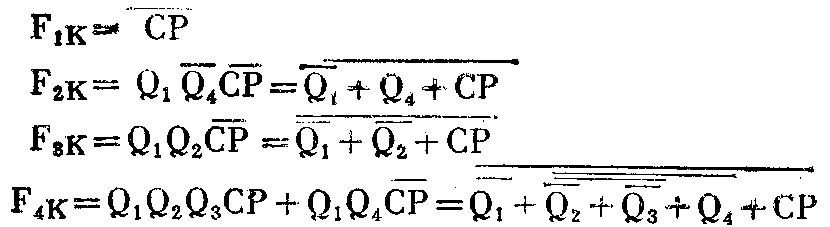
由控制方程可总结出计数与进位的规律：对于触发器F\(_{1}\)，每输入一个CP脉冲，F1就翻转一次。仅当Q\(_{1}\)=1，Q4=0时，每输入一个CP脉冲，F\(_{2}\)就翻转一次。当Q1=Q\(_{2}\)=1时，每输入一个CP脉冲，F3就翻转一次。而当Q\(_{1}\)=Q2＝Q\(_{3}\)=1时或者Q1=Q\(_{4}\)=1时，F4才在CP脉冲作用下翻转一次。下面具体分析1～10的计数过程：清零信号过后，Q\(_{4}\)～Q1的计数状态为0000，称原始状态。第一个CP脉冲来到时，F\(_{1}\)置1，Q1=1；Q-\(_{1}\)=0，Q4～Q\(_{1}\)的计数状态为0001。由于Q1=1，Q-\(_{4}\)=1，这就为下次触发F2做好了准备。第二个CP脉冲来到时有两个作用：①使F\(_{2}\)置1，Q2=1，Q-\(_{2}\)=0；②使F1置0，Q\(_{1}\)=0。计数状态为0010。因为第三个CP脉冲过后，计数状态为0011，即Q1=Q\(_{2}\)=1，所以第四个CP脉冲来到时，使得：①F3置1，Q\(_{3}\)=1；②F2置0，Q\(_{2}\)=0；③F1置0，Q\(_{1}\)=0，计数状态为0100。第八个CP脉冲来到时，F4翻转，Q\(_{1}\)=Q2=Q\(_{3}\)=0，计数状态为1000。第十个CP脉冲来到时，因在此之前Q4=1，故CP脉冲的上升沿不能触发F\(_{2}\)，F2仍为0，又因在这之前Q\(_{1}\)=Q4=1，故CP能触发F\(_{4}\)，使F4置0，Q\(_{4}\)=0，电路恢复“0000”原始状态，同时从Q4端输出一个进 位脉冲。如此循环下去，便完成了二—十进制计数。

从以上分析可以看出，在输入CP脉冲作用下，能够翻转的触发器总是同时翻转的，属同步计数器，它的特点是具有较高的计数速度。

2. 数据锁存电路：它包括四路数据锁存电路，传输门TG\(_{1}\)、TG2以及非门1、2、3组成Q\(_{1}\)数据锁存电路，TG3、TG\(_{4}\)以及门4、5、6组成Q2数据锁存电路，TG\(_{5}\)、TG6、门7、8、9为Q\(_{3}\)数据锁存电路，TG7、TG\(_{8}\)、门10、11、12为Q4数据锁存电路。下面以Q1数据锁存电路为例，介绍锁存电路的工作原理。

在数据锁存电路中，传输门的导通或截止是由锁存控制端LE的电平状态控制的，而每个传输门又有两个控制端，如Q\(_{1}\)锁存电路中，TG1左边的控制端加正极性控制电压，右边的控制端（带小圈）加负极性控制电压，TG\(_{2}\)导通，其上下两端可实现（双向）数据传送。当TG1所加控制电压与上述相反时，TG\(_{1}\)则截止，不能传送数据。当LE为“0”电平时，经门14反相后变为高电平，此高电平加到TG2的正极性电压控制端和TG\(_{1}\)的负极性电压控制端；LE的“0”信号经门14、13两次反相后变为低电平，此低电平加到TG2的负极性电压控制端和TG\(_{1}\)的正极性电压控制端，使TG2导通，TG\(_{1}\)截止。这样，计数单元中F1的Q\(_{1}\)端的数据信号通过门1～3及TG2传送到输出端M和N，即：M=Q-\(_{1}\)，N=Q1。当控制端LE为高电平“1”时，TG\(_{1}\)和TG2所加控制电压与上述刚好相反，TG\(_{1}\)导通，TG2截止。由于TG\(_{2}\)截止，Q1端的数据信号不能传送到MN端，但是，由于TG\(_{1}\)的导通，M=Q-1将通过TG\(_{1}\)反馈到门2的输入端，经门2和门1反相后使MN端仍为原来状态，也就是保持了原来已传送的数据信号，从而实现了数据锁存。其余三路锁存电路的结构原理完全相同。整个锁存电路的功能是，LE=0时，计数器Q1～Q\(_{4}\)端的数据信号可以传送到锁存器的输出端，也就是译码器输入端，LE=1时，Q1～Q\(_{4}\)端的数据信号不能传送到译码器输入端，但原来已传送的数据被锁存，不再随计数器的状态而变化。

设置锁存器的目的是为了避免在计数过程中出现不停地跳数现象，以利于读数或记录。例如，在数字频率计中，计数器是每秒计数一次，计满1秒计数器自动清零，然后再重新计数1秒，不断重复。若无锁存器，当计数器清零时将显示全零状态。看上去显示的数码就有不停地跳动现象。若在计数器清零前通过特定电路向LE端送入“1”电平，则原来数据被锁存，计数器清零后仍显示原数据，待计数器计满1秒后再向LE端送入“0”电平，将新数据送入译码器，这样显示的数码就没有跳数现象了。

3.译码、驱动、显示电路：译码器为四线至七段译码器，显示字形笔划如图3（引线排列图）所示。它由译码部分的门1～22组成。其功能就是将计数器的BCD码译成阿拉伯数码。译码器是一种组合逻辑电路，其输出状态仅取决于此时输入状态。现以笔段a为例说明一下笔段方程式的写出方法。图2中，a=C-＝K+I-…①，K=DCBA-…②，I=CBA-… ③，将式②③代入①，得a=C-=ACBD+ABC-。这里需要说明的是，门14的三个输入端中H是消隐电路的输出端，在正常显示情况下H=1，因此，上述方程式①中没有考虑H。按上述方法由图2不难写出各笔段的逻辑表达式（布尔代数式）：

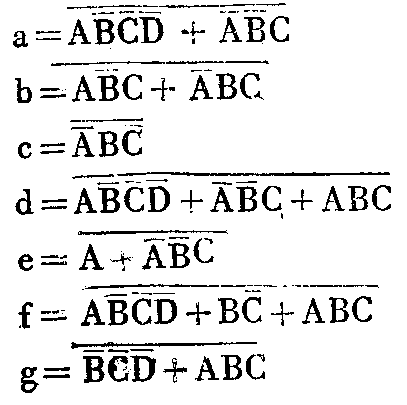
根据上述表达式也很容易得出对应于各种数据状态下七段a～g的状态。例如，当计到第七个数时，DCBA=0111，各笔段的状态分别为：a=1，b=1，c=1，d=c= f=g=0。即 a、b、c段亮，d、e、f、g不亮，显示字为7。当计数器从“0000”～“1001”变化时，显示器显示0～9。

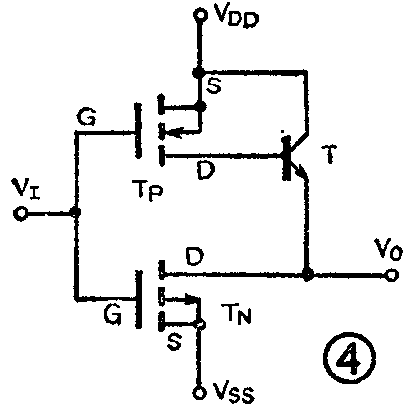
由于CMOS门电路的输出电流较小，本电路驱动级（门16～23）为MOS管与双极型晶体管复合而成，如图4所示，当输入端V\(_{I}\)=0时，MOS管TN截止，T\(_{P}\)导通，TP漏源电流I\(_{DS}\)注入双极型晶体管T的基极。T导通，使显示单元LED发光。当VI=1时，T\(_{P}\)截止，TN导通，T的基极为低电平，T截止，LED不发光。这种电路最大驱动电流达几十毫安。

4．消隐电路：消隐电路有三部分，一是显示的强迫消隐，二是小数点消隐，三是无效零消隐。强迫消隐电路比较简单，由图2可知，当消隐控制端BI为高电平“1”时，或非门24输出低电平，并同时加到门8～15的输入端，使它们均输出高电平，使门16～23均输出低电平，各显示单元均不亮，实现消隐。当dPI=0时，小数点dp被消隐。此位不是小数位将dPI接低电平“0”即可。所谓无效零消隐就是将数码中没有用的零数码灭掉。例如，一个数字仪中显示八位数0015.1020，这里15前的两个零以及最后一个零就是无效零。经无效零消隐电路后就显示为15.102，这才符合我们的书写和阅读习惯。由图2可见，如果本位不是小数点位，则dPI=0；如果我们人为地将RBI 端也接“0”电平，则门25的第3个输入端为低电平零；如果本位恰好为零数码，计数器为“0000”状态，则门25的第1、2个输入端也为低电平。也就是说，当本位为0，也不是小数点位，且RBI=0时，门25 的四个输入端全部为低电平，输出端为高电平，经门24反相后变低电平作用于门8～15的输入端，使它们均输出高电平，门16～23输出低电平，各显示单元均不亮，从而实现无效零消隐。此零是否为无效零，则应通过各位间的RBO与RBI端的正确联接确定，这一问题我们放在CL102的多位级联一节中介绍。

另外在图2中，R端为清零端，当R=1时，各计数单元F\(_{1}\)～F4均被置“0”，计数器为“0000”状态，电路显示0。ABCD为BCD码输出，分别为2\(^{0}\)、21、2\(^{2}\)、23代码，供信号检测或记录之用。V端为显示器公共阳极，改变V端电位可以改变显示器亮度。

顺便指出，CL102中计数部分与CC4518相同，译码部分与CC4511相同。

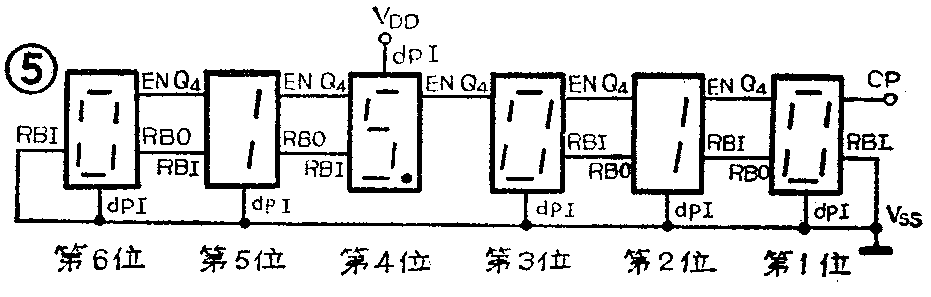
当某一装置需要多位计数显示时，可将CL102级联使用。级联时主要是考虑时钟、进位以及无效零消隐问题。进位端的连接应是低位进位端Q\(_{CO}\)与相邻高位的负脉冲时钟端EN相接，利用QCO的下降沿使高位计数。若将Q\(_{CO}\)与高位的CP端相连，利用上升沿计数，则得不到“逢十进一”的结果。这是因为当计数器计到第8个数时，QCO就有一正脉冲输出（Q\(_{4}\)由“0”变为“1”），若用它作为高位的CP信号完成的将是八进制计数。但当计到第十个数时QCO却有一负脉冲输出，因此，低位的Q\(_{CO}\)与相邻高位的EN相连完成的是十进制计数。但最低位可用上升沿也可用下降沿计数。图5是这种典型的级联方式。自动零消隐电路是这样连接的：在小数点前，最高位的RBI接“0”电平，高位的RBO与低位的RBI相连；小数点后，最低位的RBI按“0”电平，低位的RBO与高位的RBI相连。现在我们假设译码后的数码为：015.010，由于最高位RBI=0，dPI=0，且为零数码，满足消隐条件，最高位被消隐。且该位RBO=0，为相邻低位消隐提供了一个RBI=0的条件，第5位的dPI=0，但有一条件不满足就是该位不为零，故正常显示。且第5位RBO=1，这就表明第4位不能消隐。第1位RBI=0，dPI=0，且该位为零，故第一位消隐。且该位RBO=0，为第2位消隐提供了RBI=0的条件，但第2位不为零，将正常显示。且第2位RBO不为“0”，这表明第3位不能消隐，尽管它为零，所示上数就显示为15.01。（未完待续）（沙占友 苏长赞）