数字电路讲座（6）——逻辑表达式和逻辑运算

数字电路中，除了使用真值表和波形图，还常常使用数学式子来表示逻辑电路的逻辑关系。因为这种数学式子中包含有逻辑变量和逻辑运算符，所以称为逻辑函数表达式或简称逻辑表达式。逻辑表达式的优点是简单明瞭，更可贵的是它可以用逻辑代数这种数学工具进行运算和变换，达到简化电路的目的，使电路设计更简便更科学。

那么，什么是逻辑代数，它有哪些运算，它的运算又是怎样进行的呢？

逻辑代数也叫开关代数。它和普通的代数相比在意义上是不同的。首先，逻辑代数中的输入逻辑变量A、B、C……和输出逻辑变量Z并不表示数字而只表示逻辑值，而且只有0和1两种情况，它们分别表示开关的通和断、逻辑判断的真和假、脉冲的有和无等两种状态。其次，逻辑代数中的运算符及运算规律和普通代数也不同，有的虽然在形式上一致，但含义却完全不同。

逻辑代数中有三种基本运算。

（1）逻辑乘

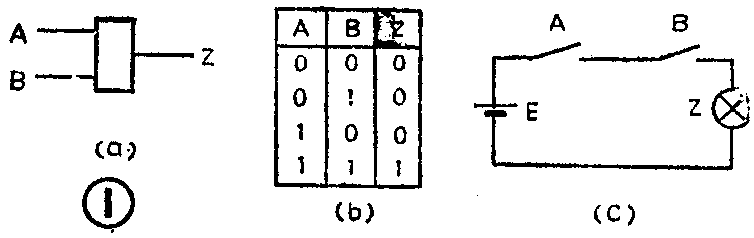
图1是与门的逻辑符号图、真值表和等效的串联开关电路图。从图看到，只有开关A与B都闭合时，灯Z才点亮；其它情况下灯都是灭的。它符合“全1出1，有0出0”的逻辑规律。与门的这种逻辑关系写成逻辑表达式是：Z=A·B读成“Z等于A乘B”。式中的“·”是逻辑乘的运算符。整个逻辑表达式表示：输出逻辑变量Z是输入逻辑变量A、B进行逻辑乘运算的结果。对照与门的真值表，逻辑乘的运算规则是：

可见它和普通代数的乘法规律在形式上是一致的。

（2）逻辑加

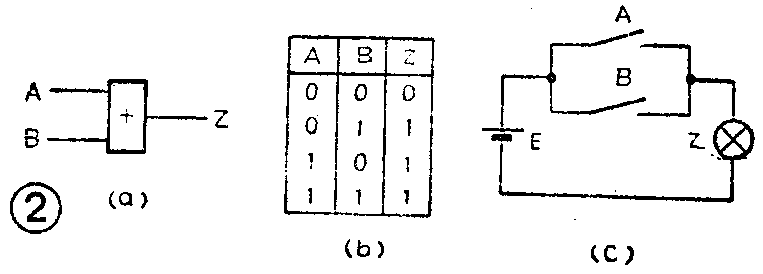
图2是或门的符号、真值表和等效的并联开关图。从图看到，当开关A或B闭合或者A、B都闭合时，灯Z点亮；当开关A、B都断开时，灯Z熄灭。它符合“有1出1，全0出0”的规律。或门的这种逻辑关系写成逻辑表达式是：Z=A＋B。读成“Z等于A加B”。式中的“＋”是逻辑加的运算符。整个逻辑表达式表示输出逻辑变量Z是输入逻辑变量A、B进行逻辑加运算的结果。对照或门的真值表可以写出逻辑加的运算规则：

其中前面三条和普通代数的加法规则在形式上是一致的，最后一条在形式上和普通代数完全不同，这是逻辑运算本身的规律决定的。只要考虑到在逻辑运算中，结果只有0和1两种可能，就不难理解1加1的结果必然仍是1。

（3）逻辑非

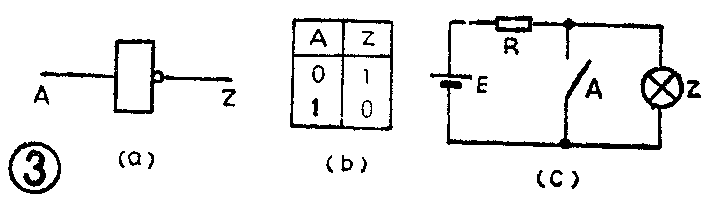
图3是非门的符号、真值表和等效图。非门的这种逻辑关系写成逻辑表达式是：Z=A-。读成“Z等于A非”。式中的“-”是逻辑非的运算符，是逻辑代数特有的。它写在A的上端表示要对A进行“非”运算，也叫“求反”运算。整个逻辑表达式表示输出逻辑变量Z是输入逻辑变量A进行“非”运算的结果。对照非门的真值表可以写出逻辑非的运算规则：

（4）逻辑代数的运算规则

逻辑代数中，在对逻辑表达式进行各种逻辑运算时,必须遵循以下的规则：

①同一个式中有乘有加时，应先乘后加。例A·B＋C·D是先做A乘B和C乘D，然后再把二项相乘的结果相加。

②逻辑表达式中如果有括号，应先做括号里面的运算。例（A＋B）·C是先做括号里的加法，然后再做乘法。

③乘法运算符有时可以省略。例A·B可写成AB。

④进行非运算时可以不用括号。例（A+B）-可写成A＋B-。在做非运算时要注意“非”号的长短，不要搞错。例AB＋CD-是先乘后加再非，而AB-＋CD-则是先乘后非再加。

我们学习数字电路知识的目的有两个，一个是根据实际问题设计出符合要求的电路；另一个是对已知的电路图进行分析，了解它的功能。设计数字电路时，一般的步骤是：根据给出的要求列出真值表。按照真值表写出逻辑表达式，再经过化简和变换得到最简逻辑表达式，最后画出它的逻辑电路图。分析数字电路时，通常是根据给出的逻辑电路写出它的逻辑表达式，再把逻辑变量代到逻辑表达式中得到它的真值表，从而分析它的逻辑功能。真值表、逻辑表达式、逻辑图是同一个逻辑函数的不同表示形式。在设计和分析数字电路时，常常会碰到从一种形式转换到另一种形式的问题。因此对于初学者来说，掌握它们之间的转换方法是必须的。

现在让我们先看看真值表和逻辑表达式之间是怎样转换的。

（1）从逻辑表达式到真值表

把逻辑表达式中各输入逻辑变量的所有的可能值都代到式中可以求出相应的输出逻辑变量的值，这个值也称为逻辑函数值。然后把输入和输出逻辑变量的对应关系列成表就得函数的真值表。例如有一个逻辑函数Z=A-B--B-，把输入变量A、B的可能值逐个代入：

把这四组变量按A、B、Z的次序画成表便是这个逻辑表达式的真值表，见图4。从这张表一看便知，它的逻辑功能相当于一个与非门。

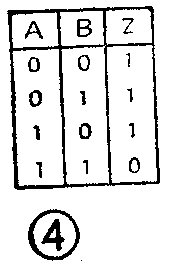
（2）从真值表到逻辑表达式

把真值表中函数值为1的变量组合取出来，输入变量如果是1就写成原变量的形式，如果是0就加上非号写成反变量的形式，然后使它们相乘得到一个乘积项。最后把所有函数值是1的乘积项都加起来，就得到这个真值表所对应的逻辑表达式。例如从与门真值表中看到：只有在A=1、B=1时，Z=1。所以它只有一个乘积项，乘积项中的A、B都是原变量，它的逻辑表达式是：Z=AB，又如图4的真值表中，函数值Z等于1的项有三个，第一个是A=0，B=0，写成乘积项是A-B-；第二个是A=0，B=1，写成A-B；第三个是A=1，B=0，写成AB-。把这三个乘积项相加便是这张真值表所对应的逻辑表达式：Z=A-B-+A-B+AB-。

（1）从逻辑图写出逻辑表达式

从逻辑图写出逻辑表达式可以按以下步骤进行：

①把电路图按左入右出（或下入上出）的规定进行整理，并按先后次序给每个门编号；

②从输入开始按每个门的逻辑功能，逐个写出它们的输出变量；

③最后一个门的输出变量就是整个电路的逻辑函数值，也就是它的逻辑表达式。

图5是经过整理并已编好号的电路图。从图看到，门1的输出是A-，门2的输出是B-，门3输出是AB-，门4输出是A-B，门5输出是AB-+A-B。所以和图5对应的逻辑表达式是：Z=A-B-。

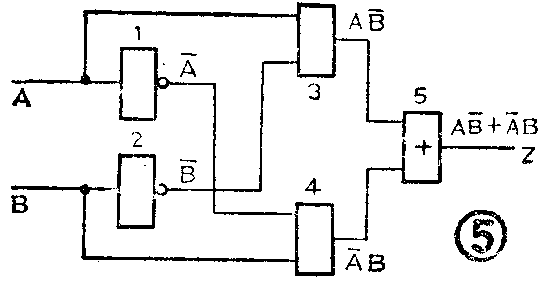
（2）从逻辑表达式画出逻辑图

从逻辑表达式画出逻辑图大致按以下的步骤：

①先弄清楚逻辑表达式中每一项以及各项之间的逻辑关系：

②按运算的次序从左到右用逻辑符号画出电路，逻辑乘用与门，逻辑加用或门，逻辑非用非门，最后得出和逻辑表达式相对应的电路图。对初学者来说，可以在每个门的输出端写上相应的逻辑式以便复核。

③最后再进行整理加工画成清晰整齐和符合规范的电路图。

例如要求画出逻辑表达式Z=A-B-+AB--B对应的电路图。分析逻辑表达式看到此式共有三项，每项是乘运算，可以用与门；三项之间是逻辑加的关系，可以用或门。所以，第一步先画成图6（a），再经过整理画成完整的电路图，如图6（b）。全部电路使用两个非门、三个与门和一个或门。

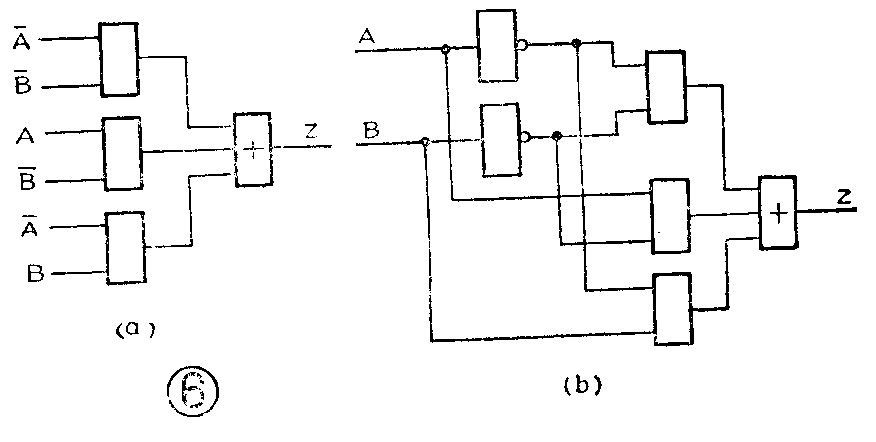
和这个电路相对应的真值表是图4。从真值表分析可以知道，它的逻辑功能是与非逻辑关系，也就是说这里用了六个门电路，实际上只需要用一个复合的与非门就可以了。可见，按真值表或逻辑表达式直接画出的逻辑电路图有时并不是最经济最合理的。通常都要对逻辑表达式进行化简或变换以后才能得到较为理想的电路图。

1．逻辑代数有哪些基本运算，它们在运算时要遵循什么规则？

2．从二输入端或门的真值表写出逻辑表达式。

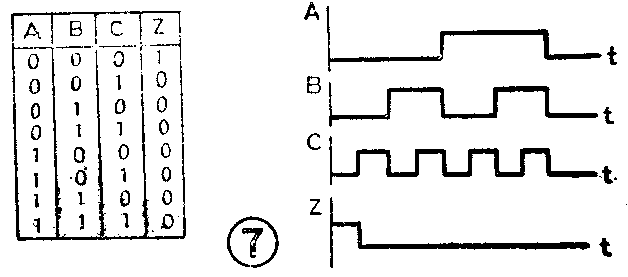
2．或非门的逻辑功能是：“有1出0，全0出1”，其真值表和波形图见图7。（俞鹤飞）