数字电路讲座（3）——基本门电路的逻辑符号和真值表

有了前面的基本门电路的基础知识，就可以进一步介绍更为复杂一些的门电路。但是为了便于读者更好地学习和掌握数字电路的知识，在学习复杂的门电路之前，先介绍门电路的逻辑符号和真值表。

一个复杂的数字电路往往使用着成百上千个门电路。如果在一张图上把每个门的具体电路都详细地画出来，那将是一张巨大的图。不仅如此，因为门电路可以是二极管的，也可以是晶体三极管的；可以是分立元件的，也可以是集成电路的，等等，于是使这张图变得更为复杂。这样的图，画起来费时，读起来费力，实在太不方便了。

实际上，分析数字电路时主要是分析它们的逻辑功能。这些逻辑功能是靠各种逻辑部件去完成的，门电路就是逻辑部件中的一种。因此在数字电路图中，一般只需表示出用的是什么逻辑部件以及这些逻辑部件之间存在什么样的逻辑关系就行了。至于每个逻辑部件内部究竟是二极管电路、晶体管电路还是其它电路组成的，完全可以不去理会它。由于这个原因，我们就人为地给各种门电路规定了标准图形符号。于是在电路图中只要见到这些符号就能认出它们代表的是什么逻辑功能的门电路。由于这些图形符号突出了数字电路的逻辑功能，使得画图、读图和分析电路大为简便，受到了大家的欢迎。这种图形符号就叫做门电路的逻辑符号。

基本门电路的逻辑符号如图1所示。图1（a）是与门的逻辑符号，A、B是输入端，这里只画了两个输入端，实际的与门可能有好几个输入端。Z是输出端，它只有一个。输入和输出之间的长方框抽象地概括了除输入、输出端以外的全部与门电路。它可能是一个二极管与门，也可能是晶体三极管与门或者是其它什么电路组成的与门。不管它是由什么电路组成的，只要它有逻辑“与”的功能就都用这个符号来表示。与门的逻辑关系是：Z端的输出信号是输入信号A、B之间逻辑“与”的结果。为了表示的方便，我们把这种关系用数学式子表示成：Z=A·B。式中符号“·”表示逻辑“与”。在下面即将介绍的逻辑代数中，它表示进行的是逻辑“乘”运算。

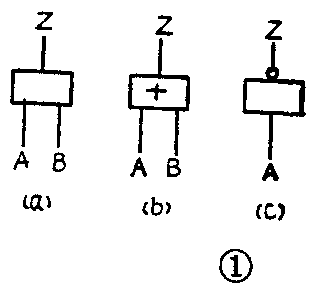
或门的逻辑符号见图1（b）。或门和与门在逻辑符号上不同的只是：或门在长方框中增加了一个“＋”号，用它表示电路具有逻辑“或”的功能。或门的逻辑关系是：Z端得到的输出信号是输入信号A、B之间逻辑“或”的结果。用数学式表示时写成：Z=A＋B。式中的符号“＋”表示逻辑“或”。在逻辑代数中，它表示进行的是逻辑“加”运算。

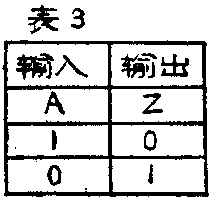
非门的逻辑符号见图1（c）。它只有一个输入端A和一个输出端Z。在输出端紧靠方框处加画了一个小圆圈，表示电路具有逻辑“非”的功能。非门的逻辑关系是：Z端得到的输出信号是对输入信号A进行逻辑“非”的结果。这种关系用数学式表示时写成：Z=A-。A上面的一小横表示逻辑“非”。在逻辑代数中，它表示Z对A进行逻辑“非”运算。

有了这些逻辑符号和数学表达式，不仅使画图、读图和分桥电路大为简便，而且由于这种规定能把电路的逻辑功能和数学联系起来，因此能使我们运用后面就要介绍的逻辑代数的方法去解决复杂的电路问题。这样就使数字电路的分析方法更加科学化了。

我们已经知道，有两个输入端的与门，按高、低电平的组合可以有四种情况：（1）A、B都是高电平；（2）A为高电平、B为低电平；（3）A为低电平、B为高电平；（4）A、B都是低电平。和这四种输入相对应地也有四种输出结果。按照与门的逻辑功能，只有第一种情况时，输出Z是高电平。其余三种情况，输出都是低电平。我们把这种逻辑关系用列表的方法表示出来就更加清楚，见表1（a）。这张表清楚地描绘出与门的输出和输入信号之间的全部对应关系。我们把这张表叫做与门的真值表。假定我们事先不知道这是个与门，但从表1（a）所反映的逻辑关系就可以判断这个真值表所对应的一定是一个与门。可见真值表对说明门电路的逻辑关系是很有用的。

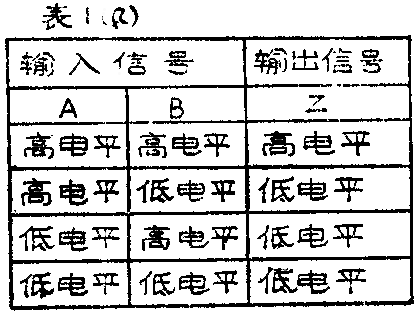
但是象表1（a）那样，用“高电平”、“低电平”这样的表示方法写起来太麻烦，也不清晰。能不能改用一种更为简单的符号来表示呢？

因为数字电路中只使用高电平和低电平两种信号，因此用符号“H”表示高电平，“L”表示低电平，可以使表示方法简化。但是我们发现，如果用数码“1”表示高电平，数码“0”表示低电平，不仅更为清晰，而且还符合数字电路中使用二进制计数的要求。如果按照这种表示方法，表1（a）可以改写成表1（b）。显然，后者的表示方法比前者更清晰、简便。所以这种表示方法已在数字电路中普遍使用。

参照与门的真值表，同样可以根据或门和非门的逻辑关系列出或门和非门的真值表。表2是或门的真值表，表3是非门的真值表。

真值表能直观地说明门电路的逻辑功能，因此已成为分析数字电路的一种重要和方便的工具。对初学者来说，必须熟悉和掌握它。

必须指出，“1”和“0”这两个符号在数字电路中，在不同的场合有不同的含义。在表示二进制数时，它们分别表示二进制数1和0。而在逻辑式和真值表中，它们并不表示数，而只是一个逻辑符号，用来表示逻辑问题中条件或结果的两种不同状态，例如“真”和“假”、“是”和“否”等等。有时为了区别或者强调它的逻辑意义，往往用黑体字1和0来表示。我们现在讨论的是门电路的逻辑关系，因此它们代表的就是逻辑“1”和逻辑“0”。

前面我们人为地规定，用“1”代表高电平，用“0”代表低电平。为什么一定要这样表示，能不能反过来用“1”代表低电平，用“0”代表高电平呢？这当然是可以的。数字电路中就是有两种不同的表示方法：一种用“1”代表高电平，用“0”代表低电平，这种表示法叫做正逻辑表示（简称正逻辑）；另一种则正好相反，用“1”代表低电平，用“0”代表高电平，这种表示法叫负逻辑表示（简称负逻辑）。

由于正逻辑和负逻辑的“1”和“0”所代表的逻辑信号正好相反，因此同一个电路在采用不同的逻辑规定时，就会有不同的逻辑关系。我们前面给出的真值表用的都是正逻辑，如果改用负逻辑表示结果又会怎样呢？下面就以与门的真值表为例加以说明。表1（b）是正逻辑与门的真值表。如果采用负逻辑，就是把这张表中的“1”换成“0”，“0”换成“1”。结果得到的一张新表是和表2完全相同的。也就是说负逻辑的与门和正逻辑的或门在逻辑功能上是完全相同的。根据同样道理可以知道：负逻辑的或门和正逻辑的与门有相同的逻辑功能。

因此，当我们在说明与门、或门的逻辑功能时，应该先明确它们采用的是正逻辑还是负逻辑。但是在习惯上，如果不加以特别的说明，一般就指的是正逻辑。例如前面介绍的与门和或门都是正逻辑与门和正逻辑或门。

在实际电路中，究竟采用哪一种逻辑规定要根据具体情况决定。通常在使用正电源的数字电路中采用正逻辑，例如NPN型晶体管的集电极电源就是正的。对于使用负电源的电路则采用负逻辑较为方便，例如PNP型晶体管的集电极电源就是负的。在有的电路中也可能同时使用两种电源，因此两种逻辑表示都被采用这种情况就称为混合逻辑。但是在学习和讨论中，一般都采用正逻辑。

1．对照真值表，说明正逻辑与门和负逻辑或门的逻辑功能是相同的。

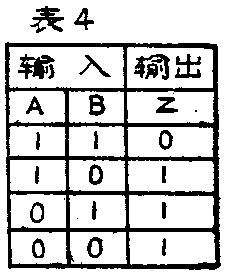
2．有一个真值表（表4），说明它的逻辑功能并画出它的逻辑符号图。如果把这个门从正逻辑变成负逻辑，它将具有什么逻辑功能？

2．如忽略晶体管的漏电流和管压降，晶体管截止时输出约为+5伏，饱和导通时输出约为0伏。（俞鹤飞）