热,是套在半导体器件脖子上的枷锁。热,会使半导体器件伏安特性发生畸变,从而导致稳定性、可靠性及寿命大为降低,甚至使它彻底损坏。因此,定量地处理电子电路中的散热问题,提高元器件的使用效率,无疑是在设计、制作以至维修中不可回避的重要环节。本文在最基本的热学理论基础上,举例分析和介绍电子电路散热装置的设计和使用方法。
热的传播及温度——热流方程
我们知道,热的传播有三种基本方式,即:传导、对流和辐射。传导是由分子运动引起的。位于高温处的分子具有较高的动能,这些动能通过分子之间的碰撞从一个传向另一个,向周围传播。甚至在散热器与空气的接触面上,能量也是靠传导方式由散热器分子传向空气分子的。在对流方式中,物质会因温差而自行流动,或者被迫流动(如鼓风),于是热能被带走。在辐射方式中能量不是靠物质运动而是靠包括紫外线到红外线的所有不同波长的电磁波来传播的。
由此可见,热是能量存在的一种方式,而热的传播就其本质而言,是能量的流动。那么,不妨把这种能量的流动叫做热流量。(简称热流)
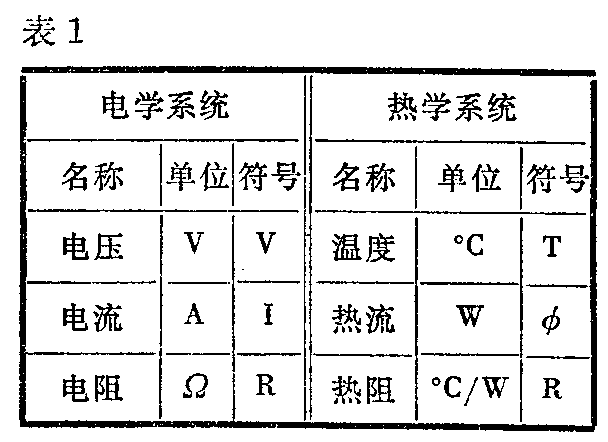
也许热流对于我们来说要比电流陌生得多。但有一点我们很清楚,如果房间里的热散不出去,房间的温度就会很高。这与电流通过较大的电阻时产生较高的电压相仿。假如把阻碍散热的能力叫热阻的话,那就可以把描述电学的量与描述热学的量列表进行对比(如表1)。不难发现,电压与温度,电流与热流以及电阻与热阻是相互对应的。这就是说,如图2a所示的热流问题可以被看作如图2b所示的电流问题来对待。
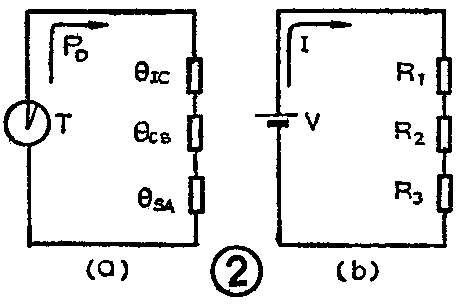
由热学的基本关系可知:温度的变化是由热流与热阻产生的,即:ΔT=φ·R
这就是温度——热流方程。不难看出,这一方程不过是欧姆定律在热学中的体现。然而正是这一方程给我们定量处理散热问题带来了理论依据。
半导体器件的发热和散热
通过上面的分析,已经对热流这一物理量有了一定的认识。既然热流是衡量能量流动的,那么以瓦特(W)作为其单位就不足为怪了。于是又使我们想起了耗散功率。大家都知道,耗散功率大的晶体管产生的热量多。事实上,前面所谓的热流正是晶体管的耗散功率。
晶体管为何会发热呢?晶体管的热量是由集电极和发射极的PN结产生的。由于集电结工作时加反向偏置,有很高的电阻,所以会产生更多的热量。实际上集电结产生的热量远远大于加正向偏压的发射结,因而可以将发射结产生的热量忽略,也就使耗散功率方程减化为:
P\(_{D}\)=IC·V\(_{CE}\)
这是P\(_{D}\)为耗散功率;IC为集电极电流;V\(_{CE}\)为加在集电极与发射极之间的电压。耗散功率PD也就是需要散发的热流。当热流遇到热阻时,就会使晶体管的温度升高。
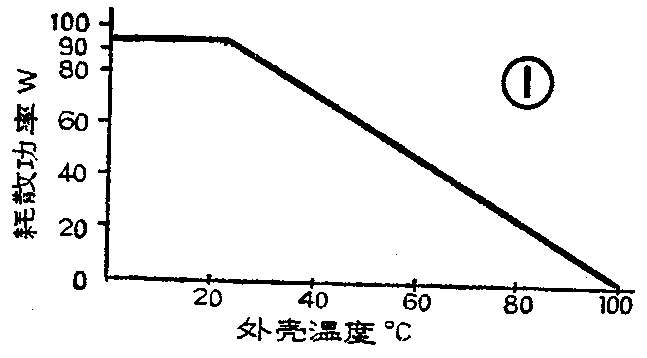
不同的半导体所承受的最高温度是不同的。如锗为85℃~100℃,而硅为150℃~200℃。但是不能让半导体器件在这么高的温度下工作,因为此时其性能已降至很低了。如图1,是一个典型的大功率晶体管的最大耗散功率与外壳温度的关系曲线。当温度低于25℃时,最大耗散功率可达90W;当高于此温度后,其最大耗散功率是线性下降,直到100℃。
散热器的选用和计算
最简便实用的散热装置就是散热器。由于一个有许多叶片的散热器会大大增加散热面积,给热的传导、对流和辐射都带来很大的方便,因而可视为小热阻元件。当其与半导体器件外壳(即大热阻元件)并联时,就象小电阻与大电阻并联一样,将使总阻值下降,从而给热流提供了更多的有效途径。就理论上而言,一个无限大的散热器可使热阻降为零。但是散热器占用空间,材料讲究,价格较高,这样就使得合理地选择散热器和计算其面积,成为设计散热装置的关键。
根据条件,可将温度——热流方程写成如下形式:
P\(_{D}\)(max)=(TJ(max)-T\(_{A}\)(max))/θJA
其中,T\(_{J}\)为晶体管所允许承受的最高表面温度;TA为要求电路工作时所处的最高环境温度;θ\(_{JA}\)为热流所经过的总热阻。这里有:
θ\(_{JA}\)=θJC+θ\(_{CS}\)+θSA
即总热阻θ\(_{JA}\)为PN结(J)到晶体管外壳(C)的热阻(θJC)、晶体管外壳(C)到散热器(S)的热阻(θ\(_{CS}\))及散热器(S)到环境空气(A)的热阻(θSA)之和(见图2a)。这里θ\(_{JC}\)可由手册上查出,而另外两个热阻就必须计算或设定。下面根据一组给定数据举例说明散热器的设计方法。
设:T\(_{A}\)(max)=60℃;TJ(max)=125℃;
I\(_{C}\)(max)=0.8A;VCE(max)=10V。
首先可得出最大耗散功率:
P\(_{D}\)(max)=IC(max)·V\(_{CE}\)(max)=8W
由于晶体管的外壳具有一定的散热能力,所以外壳不同,其自身所能承受的功率也不同。如TO-3外壳约2.8W;TO-220外壳约1.8W;TO-202外壳约1.5W;而小型TO-39和TO-92外壳只能承受约2/3W的功率。如果外壳承受的功率可满足要求,就不必使用散热器了。
设上面给定的一组数据是使用78××系列的稳压管,外壳为TO-220型,可见是必须使用散热器的。通过查手册可知7800系列θ\(_{JC}\)=5℃/W。于是将数据代人方程可得:
θ\(_{JA}\)=(TJ-T\(_{A}\))/PD=(125-60)/(0.8×10)
=8.13(℃/W)
由于θ\(_{JA}\)=θJC+θ\(_{CS}\)+θSA,所以
θ\(_{CS}\)+θSA=θ\(_{JA}\)-θJC=8.13-5=3.13(℃/W)
这时会明显地看到我们的任务无非是选取适当的散热器以保证θ\(_{CS}\)加θSA不大于3.13℃/W。然而从上面对散热器原理的分析中可知,增加散热器的面积只能减小θ\(_{SA}\)而不能减小θCS。当θ\(_{CS}\)很大时就必须使θSA很小,也就是散热器面积将取得很大。显然这是我们所不希望的。于是,在计算散热器面积之前,首要的是确定θ\(_{CS}\)。既然θCS是散热器与管壳接触面间的热阻,那么散热器与管壳的安装方式就是决定其大小的重要因素。有时为了防止短路,散热器与管壳之间要加绝缘垫。必须注意的是,绝缘垫应选用同时具有高电阻和低热阻双重特性的材料(如云母),切不可随便代换。一般为了使接触面接触紧密以降低θ\(_{CS}\),最好在接触面上涂以硅脂。在表2中列出了几种典型情况下的θCS值。可见,散热器与管壳的联接方式是安装和维修电子设备时特别应注意的。
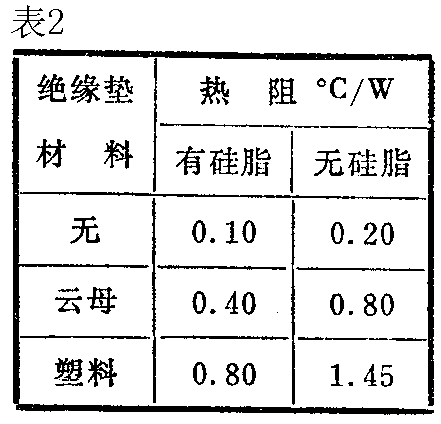
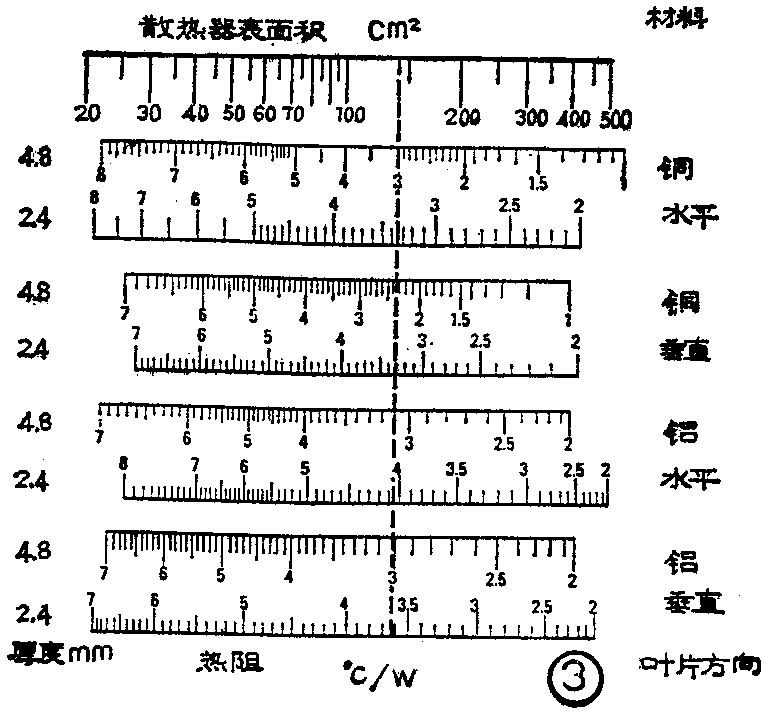
在上面的问题中,如果采用无绝缘垫并加硅脂的方式,为了计算简便且留有余量,可取θ\(_{CS}\)=0.13℃/W。于是得到θSA=3℃/W。这样,就可从图3上找出合适的散热器面积值了。由图3可知,如果使用铝材料4.8mm厚的散热器,并且打算垂直安装的话,这个散热器的表面积不应小于140cm2。
散热器使用中注意
①尽量避开其它发热元件和对温度敏感的元件。
②为了增加散热器的热辐射能力,散热器表面大多都有很薄的黑油漆、氧化物等高辐射系数的涂层。千万不可将其损坏。并在使用中应经常保持散热器表面清洁。
③特别要注意散热器与管壳的接触面及管壳平整和光洁,切不可损伤。由于管壳与散热器很难作到紧密接触,总会留有看不见的空气隙,所以安装时最好涂硅脂。
④必须加绝缘垫时,应注意绝缘垫厚度要在0.08~0.12毫米之间。
⑤尽量使散热器叶片处于垂直方向。(安文歌)