恒压源及恒流源是使用广泛的两种电源。恒压源是一种允许负载电流大幅度变化,而端电压保持不变,或者说是电源内阻很小的电源。而恒流源是允许负载电阻大幅度变化,其端电压也随之变化,却保持流过负载的电流恒定不变,也可以说恒流源是一种内阻很大的电源。
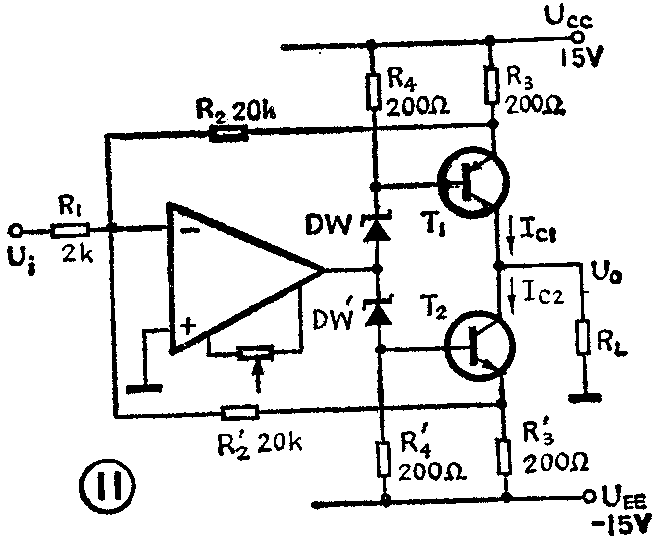
图1(a)是恒流源符号,箭头表示电流方向。图1(b)是理想恒流源的伏安特性曲线,内阻R\(_{S}\)为无穷大。实际的恒流源内阻不可能为无穷大,因而特性曲线是倾斜的。图1(c)是大家熟悉的晶体管共射极输出特性曲线。假如参变量Ib固定,则U\(_{ce}\)作大幅度变化时,而与Ib对应的集电流I\(_{C}\)却变化很小,由于r=ce/c可见,共发射极晶体管的输出阻抗是一个很大数值。换句话说,工作在线性放大区的晶体管具有很大的动态电阻。这正是恒流源所应具有的特点,正因如此,晶体管是构成各种恒流源的核心器件之一。
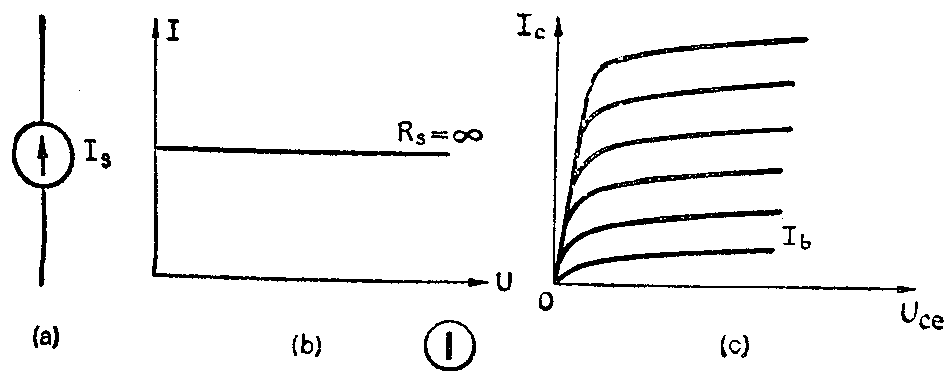
恒流源也称电流源,实质上它是一种电压到电流的转换器。图2是一恒流源的实例,图中稳压管DW为晶体管提供稳定的偏置电压,使晶体管的注入基流I\(_{b}\)不变,这样可保持IL的恒定。由于I\(_{L}\)≈(UW-U\(_{be}\))/Re,改变R\(_{e}\)的大小即可改变IL的恒定值。恒定输出电流I\(_{L}\)的大小与负载RL的大小无关,改变R\(_{L}\)的数值只会改变UC的大小,即改变U\(_{ce}\)的大小。而Uce变化时,在I\(_{b}\)不变的情况下,Ic是基本不变的,正是这种U\(_{C}\)的随动,从而保证了RL上电流I\(_{L}\)的恒定。完成电压到电流的转换。
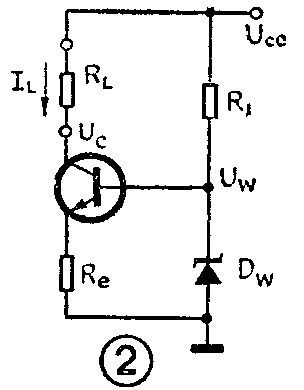
图3是常见的用结型场效应管组成的恒流源。场效应管的漏极特性曲线与晶体管的输出特性曲线极为相似。其独到之处是,输入附抗高达10\(^{8}\)Ω,温度系数小,噪声小,属于压控器件。图3之所以称为恒流源,关键在于源极电阻R\(_{S}\)。因源漏电流流过RS,其压降可为栅极提供确定的自给偏压,故R\(_{S}\)又称自偏压电阻,只要RS不变,就可保持栅源负偏压数值不变,同时也保持了漏源电流的恒定。假如R\(_{L}\)改变,只会引起漏源间电位的改变,有如Uce改变一样,并不会引起I\(_{L}\)的改变。如IL因某种原因增大,将引起R\(_{S}\)上的压降增大,这时栅源负偏压会增大,根据漏极特性曲线,|UGS|增大,源漏电流I\(_{L}\)必然下降,从而维持了IL的稳定。显然这是一种电流负反馈的效果。图3是一种极为简单而稳流性能又较好的实用恒流源。在对晶体管恒流源的工作原理有所了解之后,下面谈谈集成运放中广泛使用的恒流源。
集成运放较之分立元、器件有它本身的特点。例如,恒流水准最低到20μA的水平,要求恒流源能在几伏到几十伏电源电压下正常工作,要求恒流源温度系数小,噪声小等等。图4是典型的镜象恒流源。图中T\(_{1}\)管的b、c短接,利用发射结正向压降取代图2中的稳压管DW。何为镜象恒流源,我们可结合图4分析一下。假设β1=β\(_{2}\)=β,Ube1=U\(_{be2}\)(这在集成电路制造工艺上是很容易实现的),则有IR=I\(_{c1}\)+2Ib=I\(_{c1}\)+2Ic1/β=I\(_{c1}\)(1+2/β)……(1)式,IR称参考电流,其大小可根据恒定数值预先确定。由于I\(_{b1}\)=Ib2,β\(_{1}\)=β2,所以I\(_{L}\)=Ic1=I\(_{c2}\)(图中Ic2未标注)……(2)式,将(2)式代入(1)式,有I\(_{R}\)=IL(1+2/β)……(3)式,它表明恒定输出电流I\(_{L}\)与IR有确定的关系。当β≥100时,有I\(_{R}\)≈IL,确是互为镜象,故称为镜象恒流源。图中I\(_{L}\)的稳定,取决于IR的稳定程度,而与负载R\(_{L}\)的大小无关。RL增大时,可使U\(_{C2}\)减小,反之RL减小,可使U\(_{C2}\)增大,维持了IL的恒定。
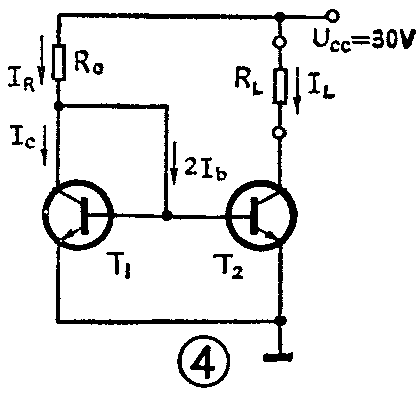
图4电路也有一定的问题,即要得到20μA水准的恒流源会遇到麻烦。由于I\(_{R}\)=(UCC-U\(_{be}\))/R0≈U\(_{CC}\)/R0,则R\(_{0}\)=UCC/I\(_{R}\)=30V/20μA=1.5MΩ。如此大的电阻,在集成电路工艺中是不能制造的。采用图5电路可以圆满地解决这一问题。图中,在恒流源输出一侧增加了一只电阻Re,这时的恒流源参考电流I\(_{R}\)与恒定电流IL就不相等了,因此它已不再是镜象关系了。通过计算可知,当R\(_{e}\)为5.07kΩ时,R0为29.5kΩ(为集成工艺所接受),可得到20μA水准的恒流源。
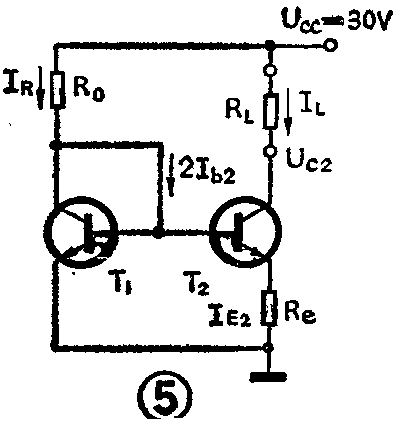
图4恒流源存在一个明显的缺点,即它们互为镜象关系的精度对电流放大系数β值的依赖性很大,例如β值是5时,参考电流I\(_{R}\)与输出电流IL的误差高达40%。特别是当一个参考电流带几路恒流输出的情况下,多路基流引入的误差将会成倍地增加。因而对图4加以改进是必要的。
图6是改进型镜象恒流源电路。采用该电路可以减小I\(_{R}\)与IL的误差。图中,I\(_{R}\)=(UCC-2U\(_{be}\))/R。IC1=I\(_{R}\)-Ib3=I\(_{R}\)-IC3/β……(1),I\(_{c3}\)=Ie3-I\(_{b3}\)= Ic1+2I\(_{b}\)-Ib3=I\(_{c1}\)(1+2/β)-Ib3……(2)将(1)式代入(2)式,有I\(_{c3}\)=(IR-I\(_{c3}\)/β)(1+2/β)- Ic3/β……(3),将(3)式展开整理有I\(_{c3}\)+2Ic3/β+ 2I\(_{c3}\)/β\(^{2}\)=IR(1+2/β),进一步整理可得I\(_{c3}\)=IR(1+2/β)/(1+2/β+2/β2)=I\(_{R}\)(β+2)/(β+2+2/β)。此时若令β=5代入公式,可得IC3=0.96I\(_{R}\)。这时输出电流IC3与参考电流仅有4%的误差。
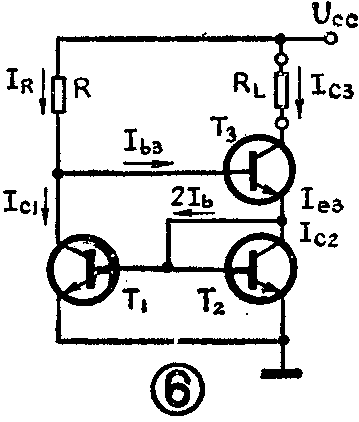
图7是集成运放中常见的由PNP管组成的改进型恒流源。该电路的恒流原理与图6相同,所不同的是图7更多地用于放大级的有源集电极负载。由于它良好的恒流特性可以提供比单管更大的输出阻抗,使单管共射放大级的增益可达数千倍。
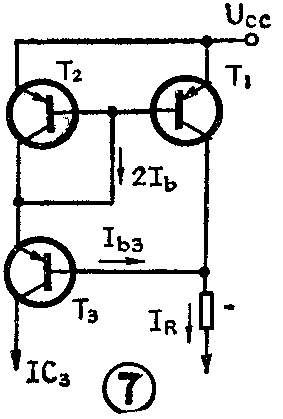
恒流源之所以能提供上百兆的输出阻抗,本质上还是由晶体管的电流传输特性所决定的。一个共基极单管放大器的输出阻抗r\(_{C}\)的表达式是其微变电压dUcb与微变电流dI\(_{C}\)之比,从电流传输特性讲,收集结电流IC受控于I\(_{b}\),收集结电压Ucb的大幅度变动几乎与I\(_{c}\)无关,它仅引起漏电流ICS的变化,而I\(_{CS}\)比IC小5到6个数量级,影响甚微,所以r\(_{C}\)是很大的,通常在10~100MΩ数量级。
用运放组成恒流源
图8是用运放组成的恒流源,它也是大家所熟悉的反相比例放大器。图中,∑点通常称虚地点(有关应地点,以前已多次介绍过)。图中有I\(_{f}\)=IR1=U\(_{Z}\)/R1。如果R\(_{f}\)为负载,则负载电流If与R\(_{f}\)的大小无关。然If恒定,则可用图8中的R\(_{f}\)=U0/I\(_{f}\)关系测量电阻Rf的数值。例如,U\(_{Z}\)=1.5V,R1=1.5kΩ,U\(_{0}\)=10V,则Rt=U\(_{0}\)/If=10V/1mA=10kΩ。再如,U\(_{0}\)=2V,则Rf=2V/1mA=2kΩ。由于电流I\(_{f}\)恒定不变,所以图8可用于线性刻度的欧姆表。
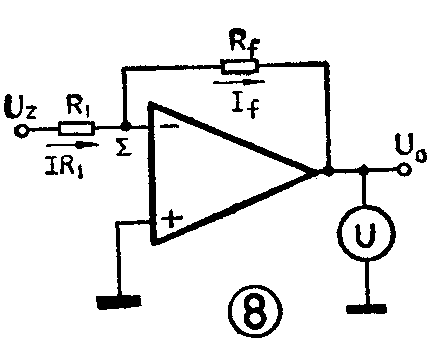
图9是一基本的恒流源。图中有I\(_{L}\)(RL+R\(_{f}\))=(UZ-I\(_{L}\)Rf\(_{od}\),展开上式有IL(R\(_{f}\)+RfA\(_{od}\)+RL)= A\(_{od}\)UZ,I\(_{L}\)=AodU\(_{z}\)/Rf(1+A\(_{od}\))+RL。由于运放的开环增益A\(_{od}\)很大,可以满足(1+Aod)R\(_{f}\)》RL,上式可简化为I\(_{L}\)≈UZ/R\(_{f}\),Rf是取样电阻。假如负载电阻R\(_{L}\)增大,使得IL减小,则R\(_{f}\)上的压降减小,运放的负端与同相端参考电压UZ的压差增大,U\(_{o}\)的增大使得IL恒定。
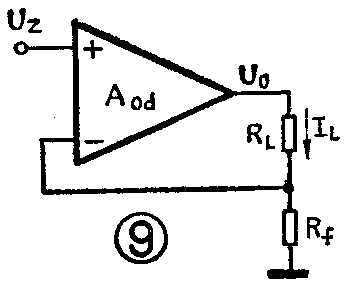
图10电路可以改善图9的频率特性和扩大恒流数值,二者恒流原理相同,可直接写出I\(_{L}\)=α·UZR\(_{f}\),α是晶体管共基极电流放大系数。
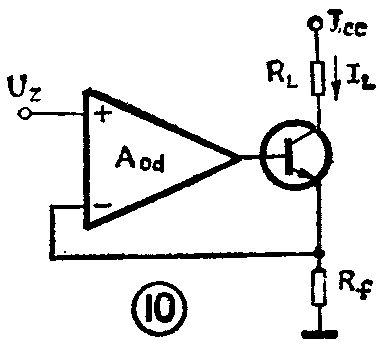
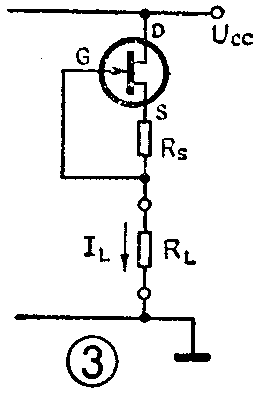
图11是一种压控型恒流源,它不同于一般恒流源,其优点是运放不承受共模电压。它的同相端接地,两只稳压管为恒流源提供静态偏置,也同时决定了最大恒流输出数值。电路上下对称配置,配以调零电位器W,因此当U\(_{i}\)开路时,输出电压Uo=0,I\(_{L}\)=0无恒流输出。两路负反馈信号的端电压即T1管射极电位与T\(_{2}\)管射极电位的电位差恒定不变。压控信号Ui的引入仅改变R\(_{3}\)及R'3 上的电压,达到用电压控制恒流数值的目的。由于两路负反馈信号相位相反,可以设想在忽略T\(_{1}\)、T2管基流时,恒流输出I\(_{L}\)与IC1、I\(_{C2}\)的电流差相等,即IL=I\(_{C1}\)-IC2。当I\(_{C1}\)或IC2中任一为零时,即可得到正向或负向最大恒流输出。(丁树凯)