CMOS集成电路 CC4017是十进制计数/时序译码器(又称为十进制计数/脉冲分配器),其用途相当广泛。下面我们作些介绍,以供大家参考。
CC4017的工作原理
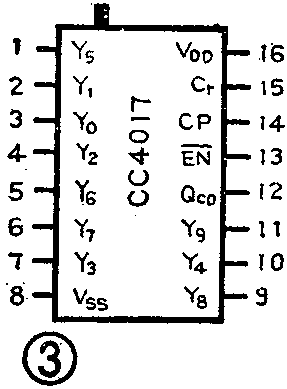
CC4017逻辑电原理图如图1所示。它主要由十进制计数电路和时序译码电路两部分组成,D触发器F\(_{1}\)~F5构成十进制约翰逊计数器,门5~门14构成时序译码电路。
约翰逊计数器的构成是比较简单的。它实质上是一种串行移位寄存器,除了第3个触发器是通过门15、门16构成的组合逻辑电路作用于D\(_{3}\)端外,其余各级均是将前一级触发器的输出端连到后一级触发器的输入端D的。计数器最后一级的Q-5端连至第一级的D端。
这个计数器有两个计数输入端,即CP端和EN-端。我们知道D触发器的CP端是上升沿有效(触发)。若用上升沿计数,信号从CP端输入。此时EN-端接“0”电平,经门2前的反向变为“1”电平。这样,当CP脉冲的上升沿到来时,经门1反相后变为负脉冲,到达门2前又反相变为正脉冲作用于门2的输入端,使门2输出正脉冲,作用于F\(_{1}\)~F5的CP端。若用下降沿计数,则CP端接“1”电平,信号从EN-端输入,下降沿到达门2前先反相变为正脉冲,结果门2同样输出正脉冲作用于各触发器的CP端。为分析方便,我们设计数器的初始状态为“00000”,并从CP端加入时钟脉冲的情况下来说明计数器的工作过程。
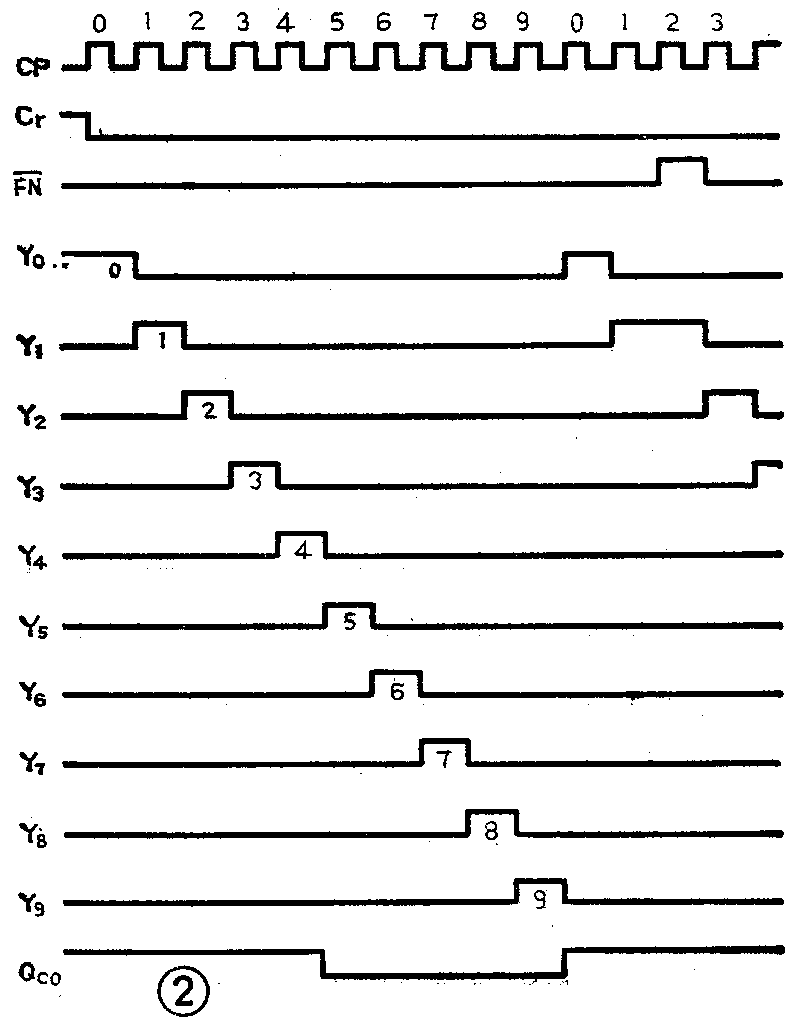
我们知道D型触发器的基本逻辑功能是:其输出端Q的状态总是与输入端D的状态相同,即Q\(_{n+1}\)=D。当计数器为“00000”状态时,F1的D\(_{1}\)端与F5的Q-\(_{5}\)端状态相同,即D1=Q-\(_{5}\)=1。D2=Q\(_{1}\)=0,D3=Q-\(_{1}\)Q-3+Q-\(_{2}\)=l-=0,D4=Q\(_{3}\)=0,D5=Q\(_{4}\)=0。当第一个CP脉冲作甩后,F1变为“1”态,F\(_{2}\)~F5仍保持“0”态,此时计数器为“10000”态。由于这时D\(_{1}\)=Q-5=1,D\(_{2}\)=Q1=1,D\(_{3}\)=Q-1Q-\(_{3}\)+Q-2=1==0,D\(_{4}\)=Q3=0,D\(_{5}\)=Q4=0。所以当第2个CP脉冲作用后,F\(_{1}\)为“1”态,F2为“1”态,F\(_{3}\)~F5保持“0”态。计数器变为“11000”状态。以此类推,当第5个CP脉冲作用后,计数器将变为“11111”状态。由上可见,随着输入脉冲个数的增加,状态为“1”的触发器的个数逐渐增多,在第5个CP脉冲作用后,状态为“1”的触发器的个数为最多,全为“1”态。此时,D\(_{1}\)=Q-5=0,D\(_{2}\)~D5=1。因此当第6个CP脉冲作用后,F\(_{1}\)变为“0”态,F2~F\(_{5}\)仍为“1”态,计数器变为“01111”状态。按上述方法继续分析,可以得出,当第7、8、9个时钟脉冲作用以后,计数器的状态将依次为“00111”、“00011”、“00001”。可见,从第6个CP脉冲开始,随着输入脉冲个数的增加,状态为“ 1”的触发器的个数逐次减少。由于第 9个CP脉冲作用后,Q1~Q\(_{4}\)=0,Q5=1,所以当第10个CP脉冲作用后,各触发器均为“0”态,计数器返回初始状态“00000”,完成一个计数循环。从下一个CP脉冲开始,又重复上述过程。
CC4017的时序译码电路也很简单。它由门 5~门14组成,共有Y\(_{0}\)~Y910个时序输出端和Qco一进位端。由图1可见,Y\(_{0}\)=Q-1Q-\(_{5}\)、Y1=Q=\(_{1}\)Q-2、Y\(_{2}\)=Q=2Q-\(_{3}\)、Y3=Q=\(_{3}\)Q-4、Y\(_{4}\)=Q=4Q-\(_{5}\)、Y5=Q=\(_{5}\)Q=1、Y\(_{6}\)=Q-1Q=\(_{2}\)、Y7=Q-\(_{2}\)Q=3、Y\(_{8}\)=Q-3Q=\(_{4}\)、Y9=Q-\(_{4}\)Q=5。由此不难得出对应于计数器各状态下的译码器的输出状态。例如,当计数器为“00000”状态时,Y\(_{0}\)=Q-1Q-\(_{5}\)=O-O-=1。当计数器为“10000”状态时,Y1=Q=\(_{1}\)Q-2=l=O-=1。显然,当计数器从“00000”状态依次变到“00001”状态时,在Y\(_{0}\)~Y9这10个输出端便得到顺序输出的正脉冲,即时序脉冲。在第10个脉冲作用后,计数器为“00000”状态,此时Qco=Q-\(_{5}\)=1,输出一个正脉冲,即进位脉冲,作为下一级的时钟脉冲信号。
图1中的Cr端为清零端。当在Cr端加上高电平或正脉冲时,计数器中各计数单元F\(_{1}\)~F5均被置零,计数器为“00000”状态。
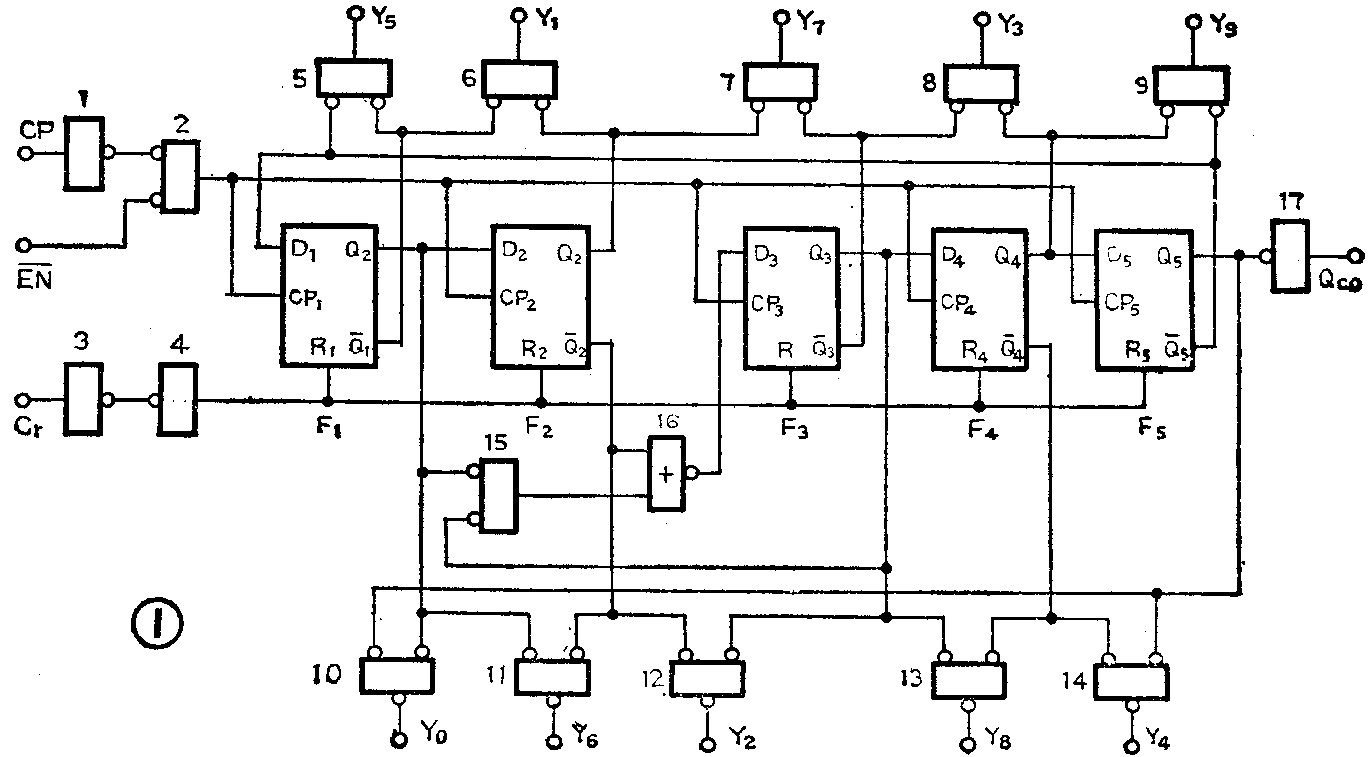
综上所述,CC4017的基本功能是对CP端输入脉冲的个数进行十进制计数,并进行时序译码,按照输入脉冲的个数顺序地将脉冲分配在Y\(_{0}\)~Y9这10个输出端,计满10个数后计数器变为零,并输出一个进位脉冲。
CC4017的应用
1、十进制计数——数码显示器:
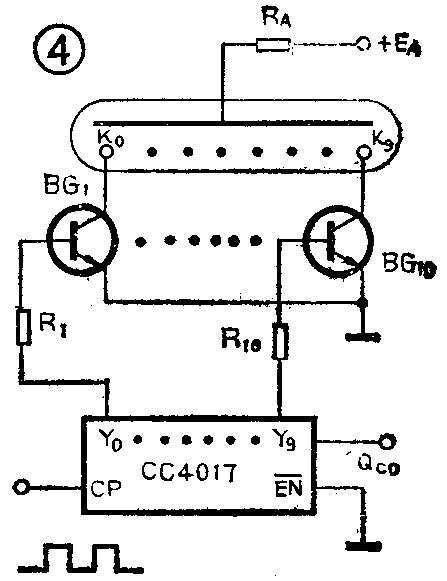
用CC4017和辉光数码管构成的十进制计数——数码显示器如图4所示。图中,数码管的公共阳极通过电阻R\(_{A}\)接在正电源EA上,当其阴极K\(_{0}\)~K9中任意一个电极与阳极之间的电压大于起辉电压时,该阴极就被点亮,并根据阴极的形状(0.1、2……9字样)显示出相应的数码。图中的晶体管BG\(_{1}\)~BG10是显示驱动管。当CC4017计到某一个数时,所对应的译码输出端输出高电平,进而使所对应的晶体管导通,将该晶体管集电极所接的数码管阴极近似接地,于是使数码管阴极与阳极之间的电压大于起辉电压,显示出相应的字形来。若将多个这样的电路按前一级的Qco端接下一级的CP端的方式串联起来,就可构成十进制计数——数码显示的多位电路了。
2、电子琴自动节奏控制器:
图5是一种比较简单的电子琴自动节奏控制器电路。它可以打出每小节两拍密度的节奏花点,并有4/4~3/4拍的拍型转换电路,因此可用于普及型电子琴或简易电子琴中。由于拍点密度为每小节两拍,故只需8个时序脉冲,图中用的是CC4017中的Y\(_{0}\)~Y78个时序脉冲输出端。用这些时序脉冲“敲击”各种打击乐模拟电路,就可打出各种花点的节奏来。
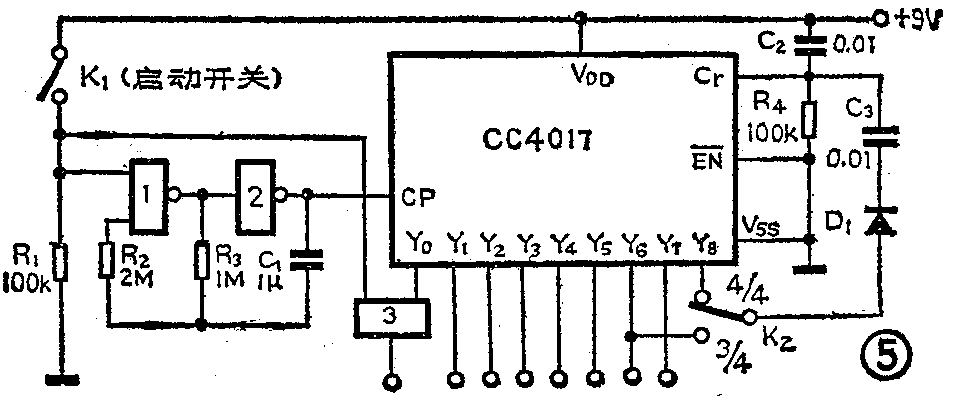
图5中,与非门1、2构成可控振荡器。在开关K\(_{1}\)闭合前,门1因有一个输入端为低电平,故输出为高电平,进而使门2输出低电平。门1输出的高电平通过R3向C\(_{1}\)充电(下正上负),并可使充电电压高于门1的转换电压。当K1闭合时,门1输出低电平,门2输出高电平,此时C\(_{1}\)通过R3放电。当C\(_{1}\)上的电压低于门1的转换电压时,门1又输出高电平,并对C1充电重复上述过程,周而复始形成振荡。在合上K\(_{1}\)后,经过一个工作周期,振荡电路即可输出第一个脉冲。
此外,电路在通电瞬间有一经C\(_{2}\)R4微分后的正脉冲作用于CC4017的Cr端,使其清零。此时Y\(_{0}\)端输出高电平,送至与门3的一个输入端。在合上K1时,门3的另一个输入端变为高电平,故Y\(_{0}\)端的高电平通过门3至输出端,产生第一个时序脉冲。这样,振荡器向CC4017的CP端送入一个个时钟脉冲时,Y1~Y\(_{8}\)便顺序输出高电平。而Y8输出高电平时,经D\(_{1}\)、C3反馈至C\(_{r}\)端,又将CC4017清零。也就是说,当第9个时序脉冲输出时,由于D1、C\(_{3}\)的反馈作用,又转为Y0输出高电平。这样便可周而复始地在Y\(_{0}\)~Y7这8个输出端得到顺序脉冲。
改变R\(_{3}\)的数值,可以调节节奏的速率。若需3/4拍的节奏,将K2置3/4档即可。这样当第4个小节开始(Y\(_{6}\)输出高电平)时,通过D1、C\(_{3}\)的作用,即可转向Y0输出高电平,从而实现了4/4至3/4拍的拍型转换。
3、用CC4017扩展定时时间:
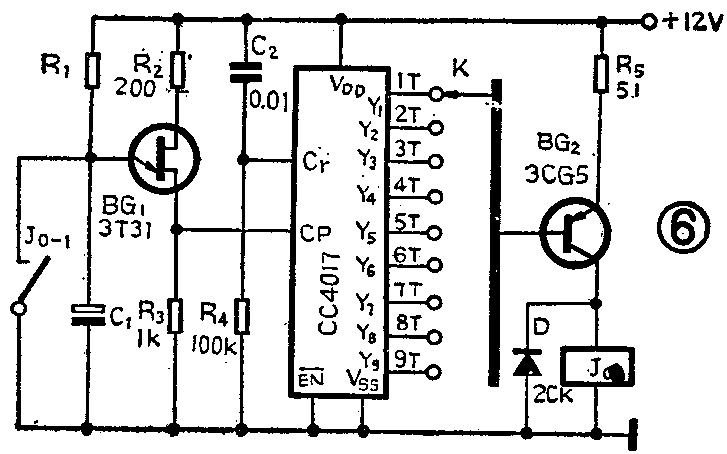
图6是用单结晶体管BT31和CC4017构成的9档定时器。其中K为定时时间选择开关。在接通电源的瞬间,有一经C\(_{2}\)R4微分后的尖脉冲作用于 CC4017的Cr端,迫使它在通电瞬间自动清零,Y\(_{0}\)输出高电平,Y1~Y\(_{9}\)输出低电平。此时,开关K无论处于哪一档位,BG2均可导通,继电器J吸合,所接用电器工作。同时,继电器J的常闭触点J\(_{0}\)-1打开,电源通过R1向C\(_{1}\)充电。经过一定的时间T,C1上的电压达到BG\(_{1}\)的峰点电压时,BG1导通,并输出一正脉冲作于用CC4017的CP端,使其Y\(_{1}\)输出高电平。若此时K处于1T档,则Y1的高电平将使 BG\(_{2}\)截止,J释放,用电器停止工作。此时常闭触点J0-1闭合,将C\(_{1}\)上的电荷放掉,以保证下一次定时的准确。若K处于其它档位,则定时时间分别是2T、3T……9T。由此可见,通过 CC4017可将单结晶体管定时时间T扩展1至8倍。
CC4017的应用相当广泛,广大爱好者只要掌握了它的基本工作原理,就能设计出更多更实用的电路来。注:图1所示,F\(_{1}\)中的Q2应为Q\(_{1}\)。(晓康)