门电路是集成电路的基础器件,也是构成各种复杂电路的重要组成部分,因而运用门电路进行逻辑设计和制作是掌握现代电子技术的重要内容。广大业余无线电爱好者和初学的同志,由于手中组件的种类和数量非常有限,若能灵活运用这些现有的组件进行各种电路实验将会给工作带来很大的方便。这里作为例子,对几种门电路的扩展与代用作一介绍。
门电路的扩展
在实际工作中,有时会遇到门电路输入端不够用的情况,这时就需要进行输入端的扩展,以增加输入端的数目。
(1)与门输入端的扩展:与门的逻辑符号如图1(a)所示。它可用逻辑表达式P=ABC……N表示,式中ABC……N表示与门各输入信号(即输入端的状态),而P则表示输出信号。与门的逻辑功能是,当全部输入ABC……N是高电平1时,输出P才是1;只要有一个输入为低电平0,输出就为0。
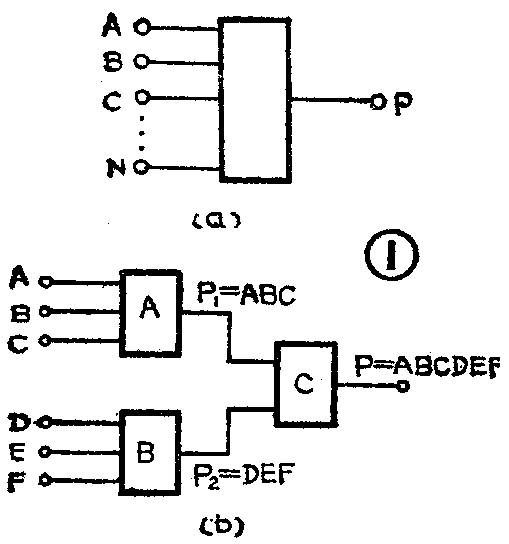
如果手头上只有两输入端和三输入端的与门,而工作中又需要四至六个输入端的与门。这时可按图1(b)方式连接,就可得到具有六输入端功能的与门。其扩展原理是P\(_{1}\)=ABC,P2=DEF,而P\(_{1}\)、P2又为与门C的输入信号,故P=P\(_{1}\)P2=ABCDEF。
(2)或门输入端的扩展:或门的逻辑符号如图2(a)所示,它可用逻辑表达式P=A+B+C+……+N表示,或门的逻辑功能是,只要输入信号中有一个是高电平1,输出信号就是1;只有所有的输入信号全为0时,输出才是0。
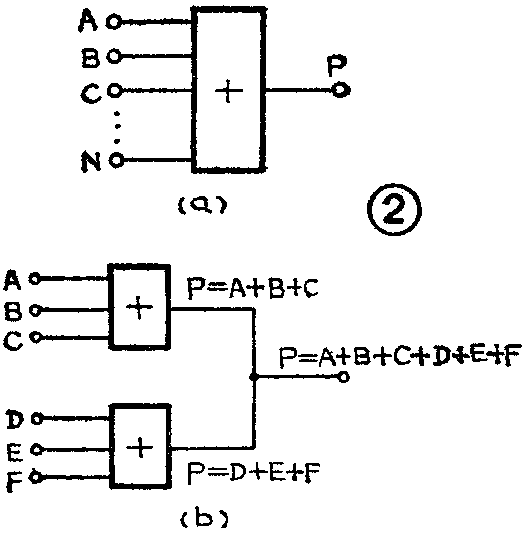
假如手头上仅有三个输入端的或门,而工作中又需要四至六个输入端的或门,这时可将三输入端或门按图2(b)方式连接,即可得到具有六输入端功能的或门。其扩展原理是,P\(_{1}\)=A+B+C,P2=D+E+F,在A~F的输入信号中,只要有一个为1,则P=1;全为0时,P=0,实现P=A+B+C+D+E+F功能。
(3)或非门输入端的扩展:或非门的逻辑符号如图3(a)所示,它可用逻辑表达式P= A+B+C+……N-表示。其逻辑功能是,只要输入信号中有一个为1,输出就为0;只有所有输入信号全为0时,输出才为1。
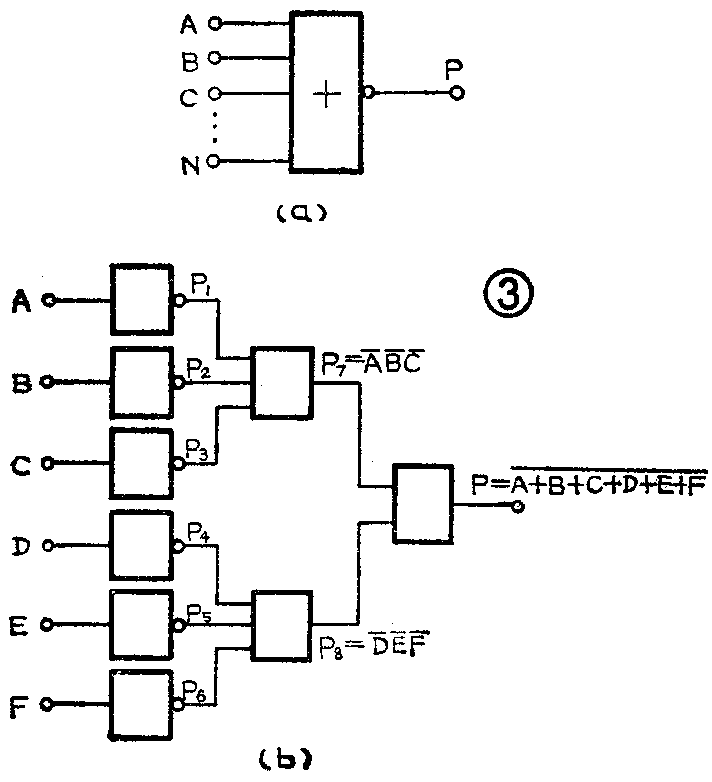
假如手头上只有与门和非门,而工作中需要四至六个输入端的或非门,这时可将与门、非门按图3(b)方式连接,便可得到具有六输入端功能的或非门。由图可知,P\(_{1}\)=A-,P2=B-,P\(_{3}\)=C-,P7=P\(_{1}\)P2P\(_{3}\)=A-B-C-。 同理P8=D-E-F-。P=P\(_{7}\)P8-B-C-D-E-F-=A+B+C+D+E+F-。由图很容易看出或非门的逻辑关系,若A~F中有一个为1,则P\(_{1}\)~P6中有一个为0,因后面都是与门,故P为0。若A~F全为0,则P\(_{1}\)~P6全为1,故P为1。
门电路的代换
在实际工作中,有时手头上没有所需用的门电路,这时可以考虑用其他的门电路组合成所需要的电路,这就是门电路的代换。
(1)用两块非门和一块与非门组成具有两输入端的或门:在图4中由于P\(_{1}\)=A-,P2=B-,P=P\(_{1}\)P2-=A-B-=A=+B==A+B。若输入信号A、B有一个为1,则A--有一个为0,对与非门来说,有一个输入为0,则输出P为1。只有A、B均为0时,A--才全为1,此时P为0。实现了或门的功能。
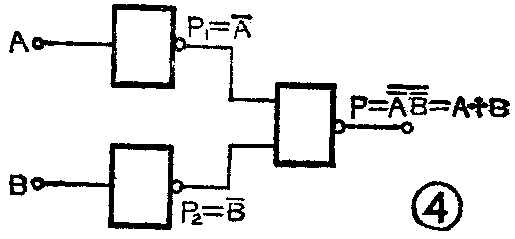
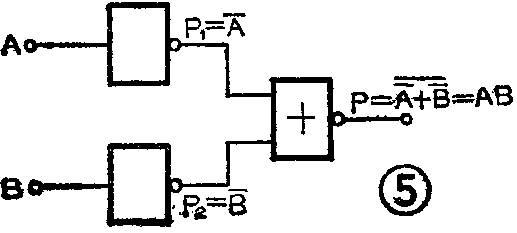
(2)用两块非门和一块或非门组成与门。在图5中,由于P\(_{1}\)=A-,P2=B-,P=P\(_{1}\)+P2-=A-+B-=A=B==AB。如果输入A、B有一个为0,则A--有一个为1,对于或非门来说,有一个输入为1,则输出P为0。只有A、B全为1时,A--全为0,对或非门来说,如果它的输入全为0,则输出P为1。这就实现了与门的功能。
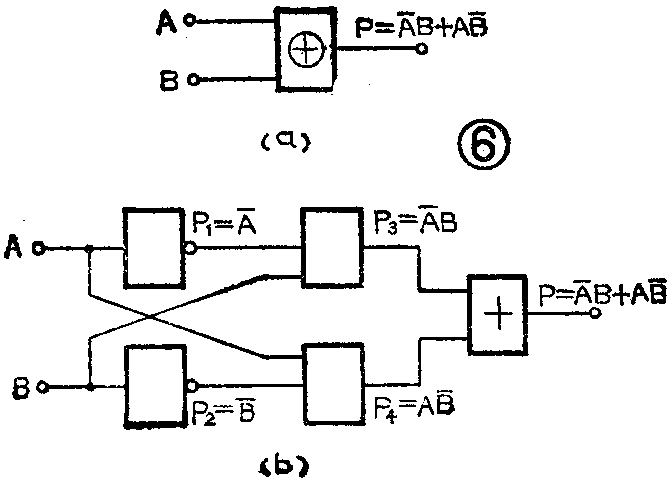
(3)用与门、非门、或门组成异或门。异或门的逻辑符号如图6(a)所示。其逻辑表达式用P=AA-B+AB-表示。异或门的逻辑功能是,当A、B相同时,输出为0;当A、B不同时,输出为1。用与门、非门和或门组成的异或门,见图6(b)。由于P\(_{1}\)=A-,P2=B-,P\(_{3}\)=A-B,P4=AB-,所以P=P\(_{3}\)+P4=A-B-。假若A、B均为0(或1),则P\(_{1}\)、P2均为1(或0),这样总可使与门的一个输入端为0,故其输出P\(_{3}\)、P4应为0。因为或门的输入全为0,故其输出P为0。若A、B有一个为0,一个为1,必使两个与门的输出一个为1,一个为0,因为或门有一个输入为1,所以输出便为1,故P也为1。这样就实现异或门的功能。
应当说明,在前面的叙述过程中,直接引用了布尔代数的运算公式。另外,这里仅对自己实际工作中用到的几种基本门电路的扩展代换作些说明。由于扩展、代换、组合的方法很多且非常灵活,故所举电路不一定简单、省料,以供一些同志参考。(周天龙)