在收音机、电视机以及电子设备中,都广泛采用由电感线圈与电容器组成的谐振回路,来选择出所需要的信号,抑制掉无用或干扰的信号。而一个谐振回路的性能如何,常常用“Q”值这样一个参数来衡量。什么是Q值,它与哪些元件及哪些因素有关?Q值对电路性能有何影响?电路对Q值有何影响等等,这一系列与Q值有关的谐振回路的问题,是每个从事无线电技术的人员及业余爱好者都需掌握的基础知识。为了说明Q值的概念,首先要从构成谐振回路的两个基本元件——电感线圈及电容器说起。
电感线圈及电容器的Q值
一个实际的电感线圈,除了具有一定的电感之外,还必然存在一些能量损耗,如果将这些损耗用一个“损耗电阻”来代替,就可以把一个实际的电感线圈画成图1那样的等效电路。图1中的损耗电阻与电感接成串联形式,用r\(_{L}\)表示电感线圈中串联损耗电阻。这种串联形式用得较多,物理概念也比较容易理解。
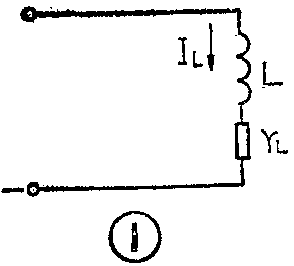
在图1中,损耗电阻r\(_{L}\)的大小就代表线圈中能量损耗的多少。显然,当信号电流IL流过r\(_{L}\)时,就要在rL上产生压降,并消耗一定的有功功率,相对来说电感中的能量就会减小。从能量损耗这个角度来看,r\(_{L}\)大就意味着电感线圈的质量低,rL小就意味着电感线圈的质量高。
基于这样的指导思想,电感线圈的Q值可以定义为:O\(_{L}\)=\(\frac{线圈中的无功功率}{线圈中的有功功率}\),即当信号电流流过线圈时,在线圈中存在的无功功率与线圈中损耗的有功功率之比。若信号的角频率为ω,信号电流为IL,则Q\(_{L}\)=I\(^{2}\)LωL/I2\(_{L}\)rL=ω\(_{L}\)/rL。此式说明:电感线圈用串联形式等效电路表示时,其Q值为线圈的感抗与串联损耗电阻之比。或者说感抗为串联损耗电阻的Q倍。显然,r\(_{L}\)越大QL就越低,r\(_{L}\)越小QL就越高,Q值的高低就成为衡量一个线圈损耗大小的参数。因此,Q值通常又称为“品质因数”。
这里也许会产生这样的问题,既然r\(_{L}\)也可以表示线圈的损耗,为什么还要引出Q值这样一个参数呢?这是由于rL是分布在线圈内部的损耗电阻,并不是一个独立的元件,测试时很难把它从线圈中分离出来。尤其是工作在高频情况下,线圈中的高频电流具有趋向在导体表面流动的特点,这种现象称为“趋肤效应”,其结果导致导体的有效面积减小,损耗电阻增加。而且随着工作频率的增高趋肤效应加剧,r\(_{L}\)值也要增大。象这样一个随频率变化的电阻,显然用万用表或一般电桥是不能测量的。而且由于rL值随频率变化,也给电感线圈的使用带来一些困难。
然而,由于感抗ωL也是一个随频率升高而增大的量,因此Q\(_{L}\)=ωL/rL在一定频率范围内就近似为一个常量,这就给测试及运用Q值这个参数带来很大的方便。在实际中,电感线圈的技术指标都不用r\(_{L}\)表示,而是用Q值表示就是这个原因。Q值的大小可以用一种专用的仪器“Q表”测出,普通线圈的Q值约为几十到一、二百左右。
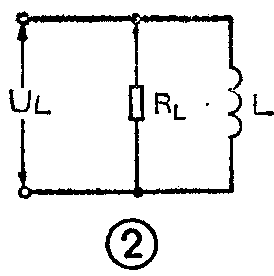
图2是采用由电感与损耗电阻并联组成的等效电路。图中R\(_{L}\)代表线圈的并联损耗电阻,它是用分流的方法消耗一部分能量来代替线圈中的能量损耗。若设UL为加在电感线圈两端的信号电压,则根据Q值的定义可得:
Q\(_{L}\)=\(\frac{线圈中的无功功率}{线圈中的有功功率}\)=UL\(^{2}\)/ωL;U\(_{L}\)2/RL=\(\frac{R}{_{L}}\)ωL。
由式可见:电感线圈用并联形式等效电路表示时,其Q值为并联损耗电阻与线圈的感抗之比。或者说,并联损耗电阻为感抗的Q倍。我们还可以看出,并联形式等效电路与串联形式等效电路相反,损耗电阻R\(_{L}\)越大QL越高,R\(_{L}\)越小QL就越低。
一个电感线圈的串联损耗电阻r\(_{L}\)与并联损耗电阻RL,都是从电感线圈两端看入的一种等效形式,因此在一定的条件下可以互相转换,便于分析电路时灵活选用。由于串联与并联等效电路所代表的是同一电感线圈,其损耗是同一个值,因而Q值也必然是同一个值。由此可以写出:QL=ωL/r\(_{L}\)=RL/ωL,进一步得到R\(_{L}\)与rL之间的关系式为R\(_{L}\)=(ωL)\(^{2}\)/rL=Q2\(_{L}\)rL。根据上述,如果已知ω、L值或Q\(_{L}\)值,再已知RL与r\(_{L}\)二者其一,就可以求出另一个值。从这里我们也可以进一步理解这两种等效电路之间的关系。例如,电感线圈的损耗电阻很小可以忽略不计时,在串联等效电路中就相当于rL=0,将r\(_{L}\)=0代入RL=(ωL)\(^{2}\)/r\(_{L}\),就可以得到RL=∞。这就是说在电感线圈的损耗电阻可以忽略不计时,在串联等效电路中相当于r\(_{L}\)短路,在并联等效电路中相当于RL开路,两种等效电路中都仅有电感L存在。
下面我们再来研究电容器的Q值。同电感线圈一样,电容器中能量损耗的大小,也可以采用Q\(_{C}\)值来衡量。当采用串联形式的等效电路时,见图3。电容器的Q值QC=\(\frac{电容器中无功功率}{电容器中有功功率}\)=I\(^{2}\)C(1;ωC)/I2cr\(_{C}\)=\(\frac{1}{ω}\)Cr\(_{C}\)。式中rC为电容器串联损耗电阻,I\(_{C}\)为流过电容器的信号电流。
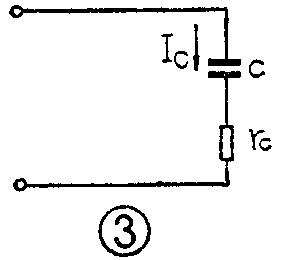
若采用并联形式的等效电路,见图4。则
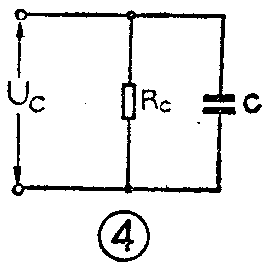
Q\(_{C}\)=\(\frac{电容器中无功功率}{电容器中有功功率}\)=U\(^{2}\)C/\(\frac{1}{ωC}\)U2\(_{C}\)/RC=ωCR\(_{C}\)。
式中R\(_{C}\)表示电容器并联损耗电阻。同样也可以推导出一个电容器在高Q情况下,RC与r\(_{C}\)的转换关系式:
R\(_{C}\)=Q\(^{2}\)CrC
电容器的损耗电阻主要取决于电容器极板之间的介质材料。一般常用的云母电容器、陶瓷电容器等,其损耗都非常小,因而Q\(_{C}\)值都很高,约为几千至几万。在许多情况下,电容器的损耗常采用“损耗角δ”来表示,并定义tgδ=1/QC。由于Q\(_{C}\)很高则tgδ很小,约为千分之几至万分之几。在组成LC谐振电路时,一般都尽量选择QC高的即tgδ小的电容器。
LC谐振回路的Q值
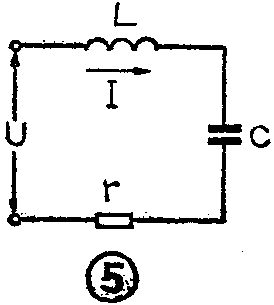
在研究了电感线圈与电容器的Q值之后,再进一步来研究谐振回路的Q值就变得十分容易了。先来看LC串联谐振回路,其电路见图5。图中L为电感线圈的等效电感,C为电容器的等效电容,r为电感线圈与电容器总的串联损耗电阻。设在角频率为ω\(_{0}\)时,谐振回路的感抗与容抗相等,即ω0L=1/ω\(_{0}\)C,回路发生串联谐振。在谐振的过程中,电感中的磁能与电容中的电能互相转换并交替出现最大值,则在谐振时串联谐振回路的Q值为:
Q=\(\frac{回路中无功功率}{回路中有功功率}\)=I\(^{2}\)ω\(_{0}\)L;I2r=\(\frac{I}{^{2}}\)(1;ω0C);I2r=ω\(_{0}\)Lr=1;ω0Cr。又因为ω\(_{0}\)L=\(\frac{1}{ω}\)0C=\(\sqrt{L;C}\),所以得出:Q=\(\frac{1}{r}\)L;C。
此式说明,串联回路谐振时,其Q值为回路的感抗或容抗与回路总的串联损耗电阻之比。也就是说,回路的感抗或容抗为回路总的串联损耗电阻的Q倍。
由于在串联谐振的情况下,回路的感抗与容抗相等互相抵消总电抗为零,即ω\(_{0}\)L=1/ω0C,总电抗X=ω\(_{0}\)L-\(\frac{1}{ω}\)0C=0。则串联回路的总阻抗呈最小值为r,回路电流I=U/r。于是,电感上的电压U\(_{L}\)=Iω0L=U;rω\(_{0}\)L=QU。电容上的电压UC=I\(\frac{1}{ω}\)\(_{0}\)C=U;r\(\frac{1}{ω}\)0C=QU。这两式说明,在串联谐振时,电感或电容上的电压为信号源电压的Q倍。因此,串联谐振又被称为电压谐振。
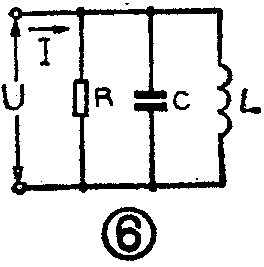
下面再来看LC并联谐振回路。其电路见图6。图中L、C分别为回路的等效电感与等效电容,R为回路总的并联损耗电阻。当电感线圈与电容器均采用并联等效电路表示时,则R=R\(_{L}\)∥RC。当信号源角频率为ω\(_{0}\)时,ω0L=1/ω\(_{0}\)C,回路发生并联谐振。此时回路的Q值为:
Q=\(\frac{回路中无功功率}{回路中有功功率}\)=U\(^{2}\)/ω\(_{0}\)L;U2/R=\(\frac{U}{^{2}}\)/1;ω0C;U2/R=\(\frac{R}{ω}\)\(_{0}\)L=ω0CR=R\(\sqrt{C;L}\)=R/\(\frac{L}{C}\),或写成R=Q\(\sqrt{L;C}\)。
上式说明,并联回路谐振时,其Q值为回路总的并联损耗电阻与回路的感抗或容抗之比。也就是说,回路总的并联损耗电阻为回路的感抗或容抗的Q倍。
由于在并联谐振的情况下,回路的总电抗为感抗与容抗并联,即X=ω\(_{0}\)L∥\(\frac{1}{ω}\)0C=ω\(_{0}\)L(-1;ω0C)/(ω\(_{0}\)L-\(\frac{1}{ω}\)0C),因为谐振时感抗与容抗相等,即分母ω\(_{0}\)L-1;ω0C=0,则总电抗X=∞。此时并联回路的总阻抗呈最大值为R,流入回路的电流I=U/R,而电感支路与电容支路的电流分别为:I\(_{L}\)=U/ω0L= IR/ω\(_{0}\)L=QI,IC=Uω\(_{0}\)C=QI。由式可见,在并联谐振时,电感及电容中的电流均为回路总电流的Q倍,所以并联谐振又称为电流谐振。
同样,谐振回路损耗电阻的并联形式与串联形式也可以互相转换。根据Q=\(\frac{1}{r}\)\(\sqrt{L;C}\)及Q=R\(\frac{L}{C}\)(两种形式都是描述同一个回路的损耗,Q值为同一值),则1;r\(\frac{\sqrt{L}}{C}\)=RC;L,于是得R=L/rc或者r=L/RC。根据这个关系式就可以进行r与R之间的互换。
上面我们分析了电感线圈、电容器的Q值,又分析了LC谐振回路的Q值。这二者之间的关系是既有联系又有区别。电感线圈与电容器的Q值,是指单个元件在任意频率下或规定测试频率下的Q值。例如收音机及电视机中的输入回路线圈、中频变压器、振荡线圈等,在产品说明书中,其Q值都被规定为一项重要的技术指标,Q值是否满足指标将直接影响机器的质量。因此,在设计或修理时,除了注意元件的数值外,还必须注意元件的Q值,最好用Q表进行测量。在实际中,也常常会发生一些与Q值有关的故障,例如回路线圈由于受潮或污垢引起Q值下降,常常会造成本机振荡停振、整机灵敏度降低。此外在制作电感线圈时,也要考虑Q值的问题,如收音机输入回路线圈要求Q值较高,除了选择合适的结构及磁芯外,主要是采用特殊的导线来绕制。中波段常用多股纱漆包线,短波段常用表面镀银的裸铜线,这都是为了减小导线的高频损耗以提高Q值。
谐振回路的Q值与元件的Q值不同,它是指在谐振的情况下,即在角频率为ω的情况下回路的Q值。在实际电路中,谐振回路的Q值除了如上所分析的与回路本身的电感线圈及电容器的Q值有关外,还与回路以外的电路有密切的关系。如信号源内阻、负载的影响等,这些问题在此就不多说了。(刘铁夫)