用单板机编制实时控制程序时,常碰到一个繁锁的问题——将十进制数转换为二进制数,如果这时身边有一个简单的计算器,这种数制的转换就变得非常容易了。
二进制数最基本的规则是逢二进一。一个十进制数转换为二进制数,常用的方法是把整数和小数部分分别转换。整数部分的转换方法是将十进制数逐次被2除,记下各次余数,直到商为0时止。将首先得到的余数作为二进制数的低位,最后得到的余数作为高位。按这样的方法排列,就是一个与十进制数等值的二进制数了。
例如:将十进制数43、375转换为二进制数先对整数部分进行转换。
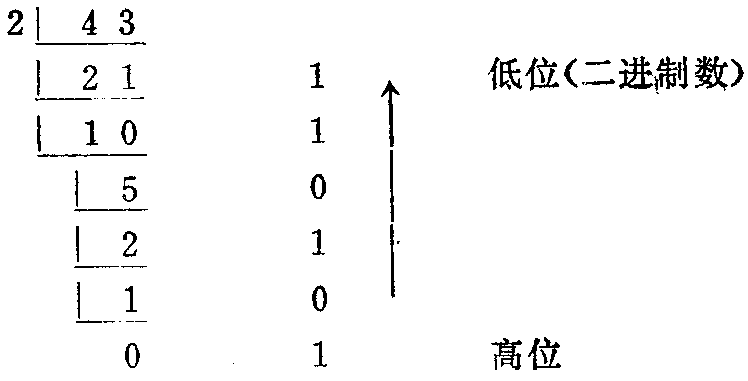
所以 (43)\(_{1}\)0=(101011)2
小数部分0.375转换为二进制数,只要把该数重复乘2,并记下进到整数部分的进位,最先得到的整数是小数点右面的第一个数,以后逐次记录,直到积为1.000,因为以后再乘2的结果,始终是零。如果有些数最后总也得不到1.000,这时只要取适当位数就可以终止。
如:0.375×2=0.75 进位为0
0.75×2=1.5 进位为1
0.5×2=1.00 进位为1
所以(0.375)\(_{1}\)0=(0.011)2,到此43.375转换完毕。将整数部分的结果和小数部分的结果相加就可得到完整的转换结果。即:(43+0.375)\(_{1}\)0=(101011+0.011)2 =(101011.011)\(_{2}\)
利用简单计算器进行十、二进制变换,就是根据这个原理进行的。只是对整数部分除2以后,判断小数部分的变化。如果是0.0增加为0.5则说有余数1,如果有0.5增加为0.75也说明有余数1,因为这是整数余1再加上原小数0.5后除2所得。同理,如果小数部分每除2一次而值不变,或者减少二分之一,则说明有余数记为0。
如:(73)\(_{1}\)0=( )2

以上两种方法所得的结果完全一致。(王振华)