在目前种类繁多的直流稳压电源中,开关型串联稳压电源及硅可控制式稳压电源的效率是比较高的。相比之下,使用最广泛的一般串联稳压直流电源的效率则是比较低的。提高这些稳压电源的效率,不仅能降低功耗,提高经济效益,而且有利于提高电子设备、整机的可靠性。
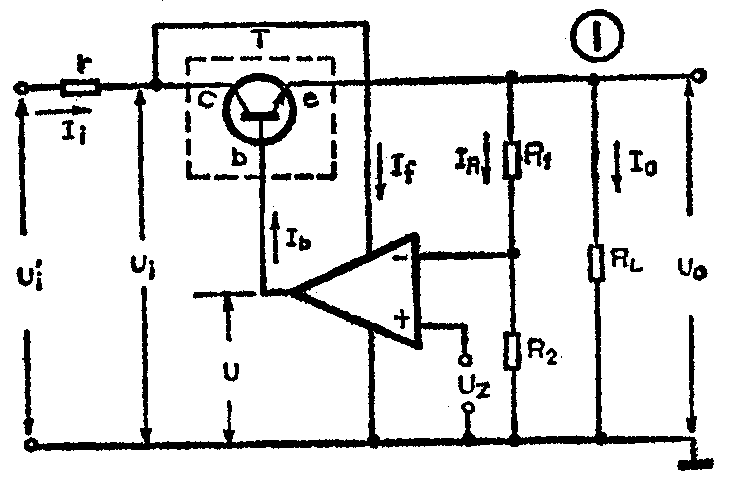
一般来说,串联反馈式稳压电源可用图1所示的简化形式来表示。其中,T为调整系统,三角部分为比较放大环节,U\(_{Z}\)表示基准电压,R1、R\(_{2}\)组成分压取样电路,RL为直流负载。另外,r表示整流滤波部分的内阻,U\(_{i}\)′为稳压电源系统的直流输入电压,Uo表示电路的输出电压。在忽略了电路的其他损耗的情况下,电路的最大效率可表示为:
η\(_{max}\)≈UoU′\(_{i}\)=Uo;U\(_{r}\)+UT+U\(_{o}\)…(1)
式中,U\(_{r}\)为整流滤波部分的直流压阵(如变压器次级绕组压降、整流管正向压降),UT为调整管集—射极间的压降U\(_{ce}\)(即Uce=U\(_{cb}\)+Ube)。由(1)式不难看出,要提高效率η\(_{max}\)可有三条途径,一是提高输出电压;二是降低整流滤波部分的压降;三是降低调整管的压降。下面我们分别加以讨论。
一、尽可能高的选择输出电压
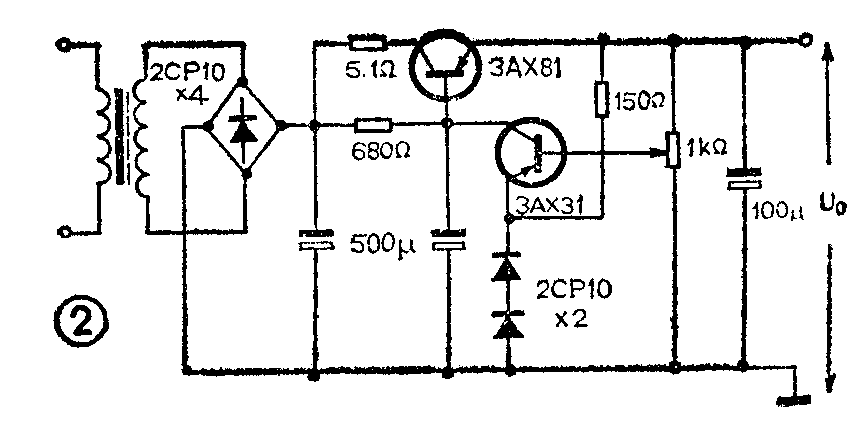
对于一个固定的整流电路来说,通常U\(_{r}\)是基本不变的,UT也相对是固定的。因此,输出电压U\(_{o}\)选择的越高,则它的效率也就越高。图2是一个一般半导体收音机稳压电源电路。图中若采用硅二极管桥式整流,则整流部分的压降约为2V左右,若忽略了变压器次级的内阻,则Ur≈2V,为便于计算,我们就设U\(_{r}\)=2V。调整管的压降通常要大于1V(对锗管而言),我们也设UT=1V。在这种情况下,若输出电压U\(_{o}\)为4.5V,则由(1)式计算出ηmax=U\(_{o}\)/(Ur+U\(_{T}\)+Uo)=4.5/(2+1+4.5)=60%,若U\(_{o}\)为6V,则效率就为66.7%。若选择Uo为9V,则效率可达到75%。上述计算忽略了电阻5.1Ω所消耗的功率,因此实际的效率要比上述的计算值稍低一些。
当然输出电压U\(_{o}\)的提高受到负载电路的限制,例如负载电路中的电解电容及晶体管耐压的限制等,但在负载电路允许的条件下,尽可能提高电源电压,对电源本身效率的提高无疑是有利的。
二、降低整流内阻的电压降
这里所说的整流内阻r,包括变压器次级绕组的直流电阻,及整流二极管的正向电阻。通常在小电流情况下,绕组的直流电阻可以忽略不计。降低整流管的电压降可采取两个措施:其一是改桥式整流为全波整流,这样压降可降低一半,若再将全波整流二极管采用锗元件,则因锗二极管的压降比硅管低,而使压降进一步降低一半。仍以图2为例,假定U\(_{T}\)为1V,Uo为4.5V,采用硅全桥整流时,U\(_{r}\)为2V,则此时ηmax=4.51+2+4.5=60%;若将电路改为锗管全波整流,此时U\(_{r}\)为0.5V,则ηmax=4.5;0.5+1+1.5=75%。当然,锗整流元件的反向电流比硅元件的要大一些。但问题不大,因在低电压的情况下,反向损耗可以忽略不计。
三、降低调整系统的电压降U\(_{T}\)
调整管的管压降受限于管子的输出功率及线性工作范围。也就是说,它必须大于管子的饱和压降才能使它工作在线性范围内,另一方面则要小于管子的击穿电压。如果单纯从提高效率来考虑,U\(_{T}\)应取下限,即大于管子的饱和压降即可。对锗管来说,一般选UT为1~2V,而硅调整管则要选U\(_{T}\)为2~4V左右。故在低输出电压的情况下,若用锗调整管代替硅调整管,则会对提高效率有利。我们仍以图2为例,假定Ur选最低值0.5V,U\(_{o}\)为4.5V,若调整管为硅管UT为2V,则η\(_{max}\)=64.3%。如将调整管改为锗管,则UT为1V,此时η\(_{max}\)=75%。
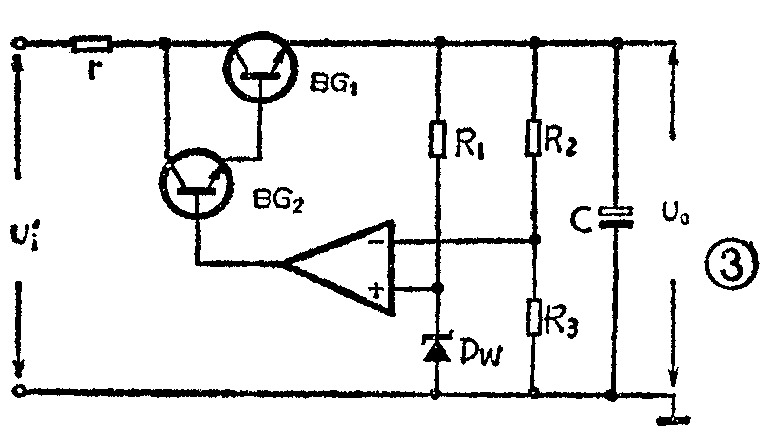
上面讨论的是调整管为单一管的情况。然而在一般情况下,调整环节均采用复合管的形式,见图3。图3所示电路为串联负反馈稳压电源的最一般形式,由于它是用电压源控制调整管起作用,故称之为电压控制型稳压电源。由于图中的调整管采用了复合管 (两只晶体管复合成达林顿)形式,U\(_{T}\)就要增加0.7V,即UT=U\(_{be1}\)+Uce2=0.7+2=2.7V。若U\(_{r}\)为2V,Uo选12V,则此时η\(_{max}\)=122+2.7+12=72%。
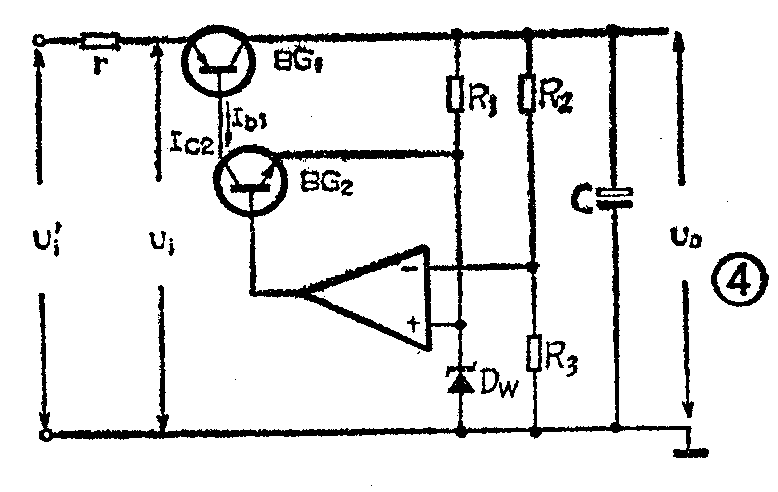
如果将调整管基极的控制形式由电压控制改为电流控制(即调整管的基极是由电流源激励的),那么它的效率会大大提高,其电路如图4所示。由图可见,比较放大器的输出端没有直接接在调整管的基极,而是经BG\(_{2}\)转换成电流信号(比较放大器输出电压U的变化,引起BG2集电极电流的变化)后再接至调整管的基极。因调整管基极与BG\(_{2}\)的集电极串接,故Ib1=I\(_{c2}\),电压U的变化导致Ib1的变化,从而调节了U\(_{ce}\)。在这里起调整作用的是调整管的基极电流,若BG1的直流放大倍数为β,则电路的输出电流I\(_{o}\)=βIb1,电路的输出电压为U\(_{o}\)=IoR\(_{L}\)=Ib1β·R\(_{L}\)。
当因某种因素引起输出电压U\(_{o}\)降低时,会使比较放大器输出电压U上升,BG2集电极电流随之增大,I\(_{b1}\)也增大,Io(=βI\(_{b1}\))增大,使Uo升高,最后使得输出电压保持不变。当然,反之也是一样。在这个电路中,调整管的集—射极之间的电压U\(_{ce}\)为0.5V,电路即可正常工作。若选Ur为0.5V,U\(_{o}\)为12V,则ηmax=12/(0.5+0.5+12)=92.3%。
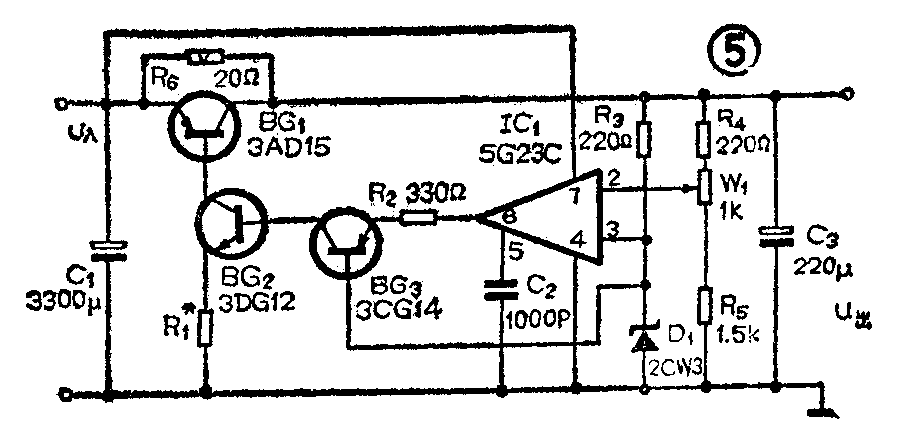
图5所示电路就是这种高效率稳压电源的一个例子,它适用于一般的12寸黑白电视机电源,采用这种电源可使电视机的功耗下降三分之一。
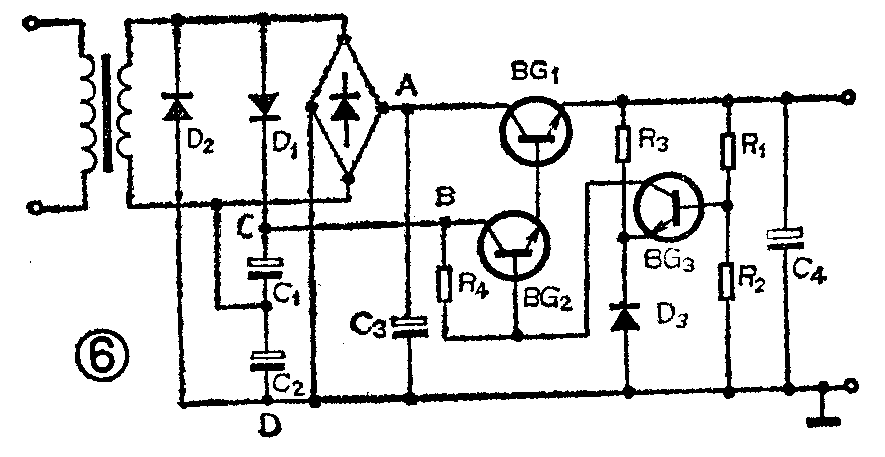
对于一般如图3所示的串联稳压电源,为了提高其精度,U\(_{T}\)往往选用得比较大,UT的增大与效率的提高相矛盾。为了解决这个矛盾,常常采用辅助稳压电源。即除主调整管外,其他管子的供电是采用另外辅助电源,由于辅助电源的电压可提高,可以提高电源的精度,而主调整管的输入电压可相对偏低,以提高电源的效率。因辅助电源负载电流较小,故可用主绕组进行倍压整流来获得,其电路如图6所示。其中,D\(_{1}\)、D2、C\(_{1}\)、C2组成倍压整流滤波电路,以利于提高精度。而调整管BG\(_{1}\)的输入电压则由主绕组经桥式整流后直接取得。这样以利于提高效率。电路仅增加了四个元件,但它同时获得了精度和效率的提高。(符龙须 朱海宇)