霍尔集成电路的原理及应用

霍尔集成电路是在霍尔效应原理基础上，利用集成电路技术制成的。它能感知一切与磁信息有关的物理量，而输出可以实际应用的电信息。所以，霍尔集成电路既是一种集成电路，又是一种磁敏传感器。

当一块通有电流的金属或半导体薄片垂直地置于磁场中时，薄片两侧由此会产生出电位差，此现象即称霍尔效应。两侧间的电位差称为霍尔电势。

实验证明，霍尔电势与外加磁场的磁感应强度B、薄片中通过的电流I成正比，与薄片的厚度成反比即

式中K称为霍尔系数，它与薄片的材料有关。

金属的霍尔系数很小，因此它的霍尔效应就很弱。而半导体中的霍尔效应较强，用它们做成薄片形的霍尔元件，可得到较大的霍尔电势。但既使霍尔电势较大的半导体材料，如砷化铟（InAs），其霍尔电势一般也只能达到几十毫伏。为此霍尔集成电路利用集成电路技术将霍尔元件、放大电路或开关电路等集成在同一个半导体基片上，做成线性或开关输出的电路。

霍尔集成电路可按输出端功能和构成霍尔集成电路的有源元件类型分类。按输出端功能可分为开关型和线性型霍尔电路；按有源元件类型可分为双极型和MOS型霍尔电路。我们这里仅介绍双极型工艺结构的霍尔电路。

双极型霍尔开关集成电路 是利用双极型集成电路技术在同一硅基片上集成霍尔元件、放大电路、整形电路和开关输出电路等。其基本功能是将磁输入信号转换成开关状态输出。实际的霍尔开关电路输出与输入磁场的关系有两种情况：单向磁场工作型和双向磁场工作型。

图1是单向工作型的双极霍尔开关集成电路的原理线路图和框图。图中H是霍尔元件，它在0.5特斯拉的磁场下，每毫安电流下约输出几毫伏至十几毫伏的霍尔电势。T\(_{1}\)、T2组成差分放大器，它将输入的霍尔电势差分放大，其放大倍数约几十倍。T\(_{3}\)、T4组成施密特触发器，将差分放大了的霍尔电势鉴幅后整形为短形脉冲输出。最后一部分是输出电路，其中T\(_{5}\)、T6是由PNP和NPN管组成的复合放大电路，将脉冲放大。T\(_{7}\)、T8则为双集电极开路输出电路（也可采用单集电极开路输出）。霍尔开关电路一般均设计成集电极开路输出结构，以便使霍尔开关电路的输出易于和其它类型的数字电路直接接口，增加输出端的灵活性。

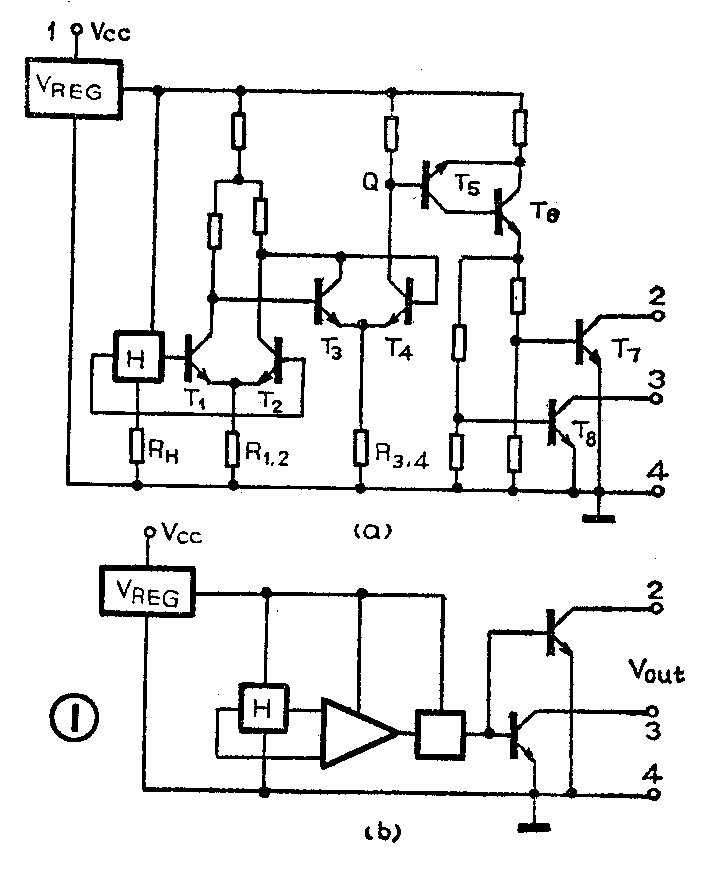
单向与双向工作型霍尔开关集成电路的主要区别在于施密特触发器的类型。图1中的施密特触发器是一种单稳态触发器。如在T\(_{3}\)管的集电极采取和T4管同样的接法，并仿照T\(_{5}\)、T6再接一组输出的话，就构成了双稳态施密特触发器，霍尔开关电路即以双向型磁场工作。

双极型霍尔线性集成电路 线性型霍尔集成电路的输出电压随外加磁场强度的变化而连续地、线性地变化。它的特点是灵敏度高，输出动态范围宽，线性度好。图2是一种简单的霍尔线性集成电路的原理性线路和结构框图。图中，T\(_{1}\)、T2是第一级差分放大器，射极电阻R\(_{1}\)、R2的接入是利用其负反馈作用展宽电路的线性范围。T\(_{5}\)、T6是第二级差分放大器，这样总放大倍数可达数百倍。

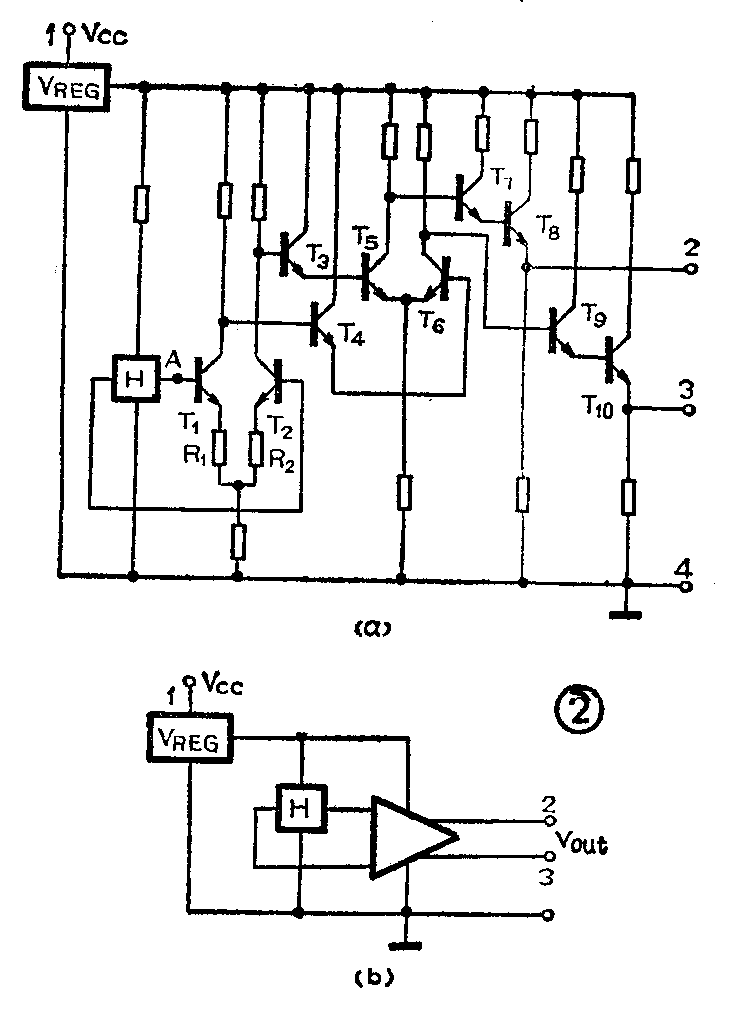
由于工艺、材料和版图等因素的影响，在不加外磁场时，霍尔元件的输出常不为零，即存在着失调电压。此失调电压经两级放大后，可以达到可观的数值。为此，线性电路中常在A点引出外接点见图3，利用桥路平衡原理，在此外接点和地之间接入电位器进行补偿（即调零）。同时，A点引出后，还可通过反馈电阻来改变电路的灵敏度，使电路的应用更加灵活。

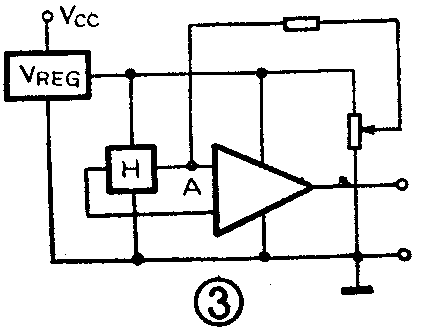
霍尔集成电路的封装形式 以封装材料分为塑料封装和陶瓷封装两种；以外形分有扁平单列式和双列直插式两种。扁平单列式常见的只有三脚、四脚两种见图4，双列直播式的脚数则有多种，常见的是八脚（每边四脚），如电路设计时引出的外接点多，也可以有更多的引出脚。

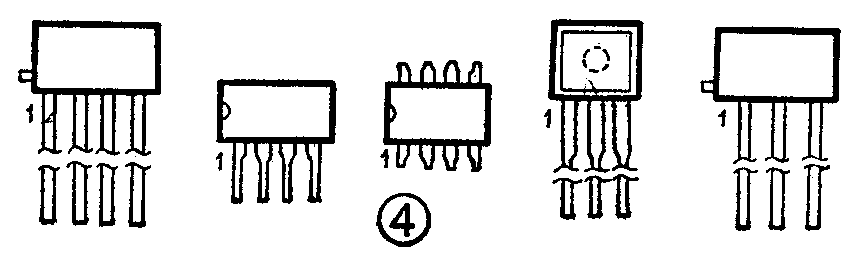
霍尔集成电路的特性 霍尔电路是磁电转换器件，其输入端是以磁感应强度B来表征的。输出端有开关型和线性型输出之分。

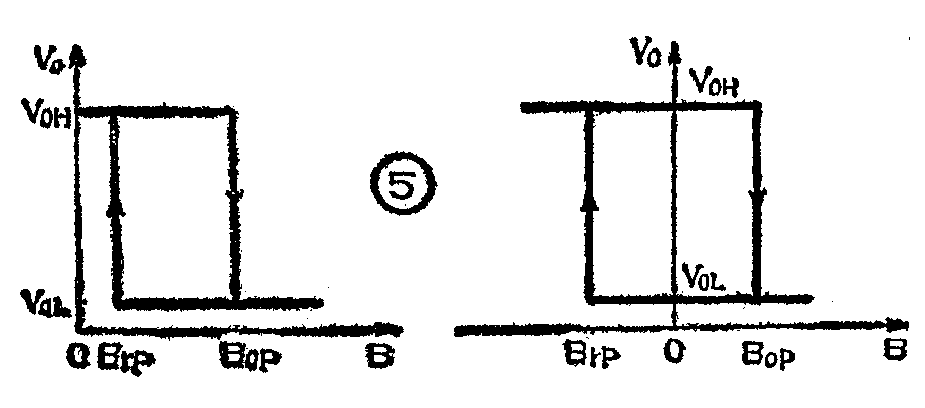
1．开关型霍尔电路的转移特性：图5是单向磁场和双向磁场工作的开关型霍尔电路的转移特性曲线。曲线表明，当B增加到B＝B\(_{op}\)时，输出V0立即变为低电平，因此称B\(_{op}\)点为导通点。当继续增加B时，V0保持低电平不变。当B降到B＝B\(_{rp}\)处，V0立即从低电平跳到高电平，此点称为释放点。继续降低B，V\(_{0}\)维持高电平不变。不同型号的霍尔开关电路，Bop与B\(_{rp}\)各不相同，它们之间存在一个磁感应强度的回差即ΔB＝Bop\(_{rp}\)，称ΔB为回差宽度。通常均以Bop和ΔB这两个参数来衡量电路的转移性能。B\(_{op}\)愈小，则电路灵敏度愈高；ΔB愈大，则电路抗干扰能力愈强。开关型的电路频率上限不是决定于霍尔效应本身，而是电路中施密特触发器的频率特性范围。所以霍尔开关电路通常的频率特性约为100kHz。

2．线性型霍尔电路的磁电转移特性为一斜线（线性区），磁场绝对值过大时曲线趋于平坦，表示此时霍尔电路已脱离线性区。（未完待续）（顾文照 朱云）