大家知道,交流电的大小和方向都是随时间变化的。其中,变化规律符合正弦函数关系的就叫做正弦交流电。正弦交流电的电流(或电压)的波形如图所示。
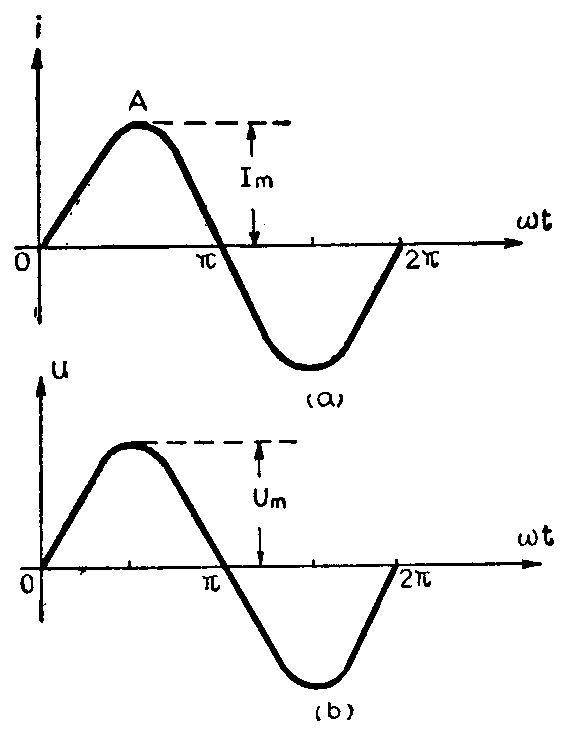
正弦交流电由零变化到最大(图中A点)时的幅度叫峰值,也叫振幅或最大值。峰值电流用I\(_{m}\)表示,见图(a)。峰值电压用Um表示,如图(b)。
如果已知某正弦交流电的峰值为I\(_{m}\)(或Um),则这个正弦交流电可用数学式表示为:
i=I\(_{m}\)sinωt或u=Umsimωt
交流电通过电阻性负载时,会消耗电能而作功(例如使电炉发热,使电灯发光等)。如果让一个交流电和一个直流电分别作用于阻值相同的两个电阻,且在交流电一个周期的时间内它们在电阻上产生的热量相等,那么从能量转换的角度来看,这个交流电与这个直流电是等效的。因此,定义该直流电压U为交流电压的有效值,同理定义该直流电流I为交流电流的有效值。
正弦交流电的有效值为多大呢?这可根据它的定义求出来。
在正弦交流电压的一个周期T中,直流电压所作的功W为:

它在一个周期中的平均值就是正弦交流电的功率P。上式中第一项为常数,平均值就是这个常数本身;第二项是周期为T/2的余弦函数,T是它的两个周期, 由于余弦函数是对称的;故在T内第二项的平均值为零。因此:
P=U\(^{2}\)\(_{m}\)/2R
正弦交流电在一个周期T中所作的功为:
W′=U\(^{2}\)\(_{m}\)T/2R
根据有效值的定义,
W′=W,即\(\frac{U}{^{2}}\)TR=U2\(_{m}\)T;2R
所以U=\(\frac{U}{_{m}}\)\(\sqrt{2}\)
同理:I=\(\frac{I}{_{m}}\)\(\sqrt{2}\)
我们知道,电流是单位时间内通过导体截面的电量。正弦交流电流的大小和方向是变化着的,在正半周内流过去一定的电量,在负半周内则流回来同样多的电量,因此正弦交流电在一个完整周期内的平均值为零,不能说明正弦交流电流的大小。但是它的绝对值的平均值I\(_{p}\)不等于零,且振幅越大,Ip也越大,即I\(_{p}\)可以表示正弦交流电流的大小;因此称Ip为正弦交流电流的平均值。同理,正弦交流电压在一个周期中绝对值的平均值U\(_{p}\)称为正弦交流电压的平均值。由于正弦交流电的正、负半周是对称的,一个周期内绝对值的平均值等于正半周的平均值,所以正弦交流电的平均值可按正半周计算。通过数学式(从略)可以证明:
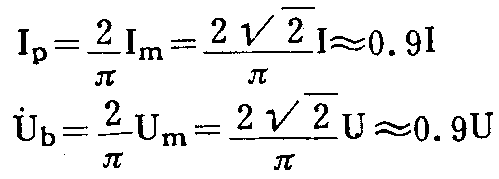
将以上结论归纳一下,可知正弦交流电的峰值、有效值、平均值三者之间的关系为:
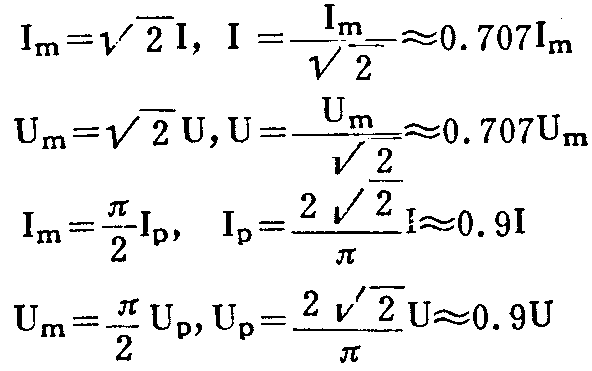
由此可见,正弦交流电的峰值比有效值大,有效值又比平均值大。通常在不加说明的情况下,正弦交流电的大小都是指它的有效值。例如,我们平时所用的220V的正弦交流电压,就是指它的有效值为220V。用交流电压表、交流电流表所测出的数值,一般也是有效值。例如万用表上的交流电压、交流电流刻度就是按正弦交流电的有效值设计的。由上述结论可知,有效电压值为220伏的交流电,它的峰值是U\(_{m}\)=\(\sqrt{2}\)U=1.414×220=311伏;它的平均值是Up=22πU=0.9U=0.9×220=198伏。(杨百一)