在设计程序时,往往会碰上看来很简单,但实际上又较难解决的问题,这时就需大家动脑筋,想一些小技巧来解决。比如下例:
〔例1〕 不允许使用第三个变量,编一段程序来交换变量A和变量B中的值。
很多教师在讲解两变量交换值的问题时,都喜欢使用这样一个生活中的例子:有两瓶墨水,一瓶是红颜色的,另一瓶是黑颜色的。怎样才能交换这两个瓶子中的墨水呢?显然,必须借助于第三个瓶子,如图1。
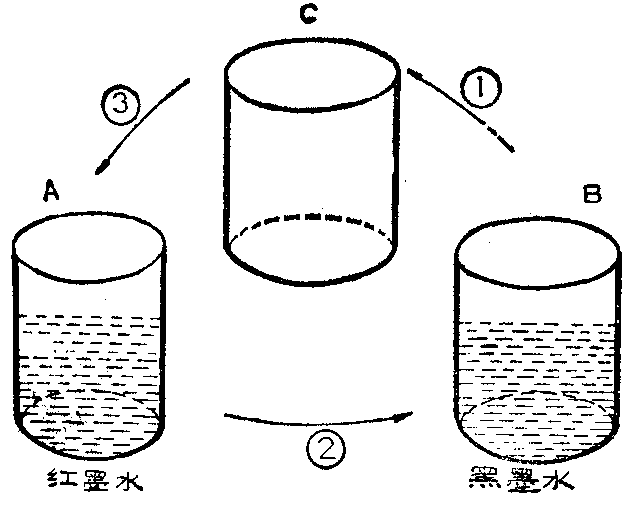
先作第一步,将B瓶中的黑墨水倒入空瓶C中,这时B瓶就空出来了,再作第二步,将A瓶中的红墨水倒入B瓶中,这样A瓶又空出来了,最后,作第三步,将C瓶中的黑墨水倒入A瓶中。经过这样一个过程,A瓶中的红墨水和B瓶中的黑墨水就相互交换了容器。把这样一个生活中的例子写成程序,正好完成了变量A的值和变量B的值相互交换的问题。程序如下:
10 LET C=B
20 LET B=A
30 LET A=C
看来,不使用第三个变量似乎无法交换两变量的值了。如何解答例1呢?这就需要借助于一点小技巧了,请看下列程序:
10 INPUT A,B
20 LET A=A+B
30 LET B=A-B
40 LET A=A-B
50 PRINT A,B
语句10为变量A和变量B从键盘上提供两个值,语句20将变量A和变量B的值相加后送入变量A中,显然变量A以前的值被破坏了,但还能不能找回来呢?语句30回答了这个问题, A—B正好恢复了以前变量A中的值,将该值赋给变量B。语句40中的A-B正好给出变量B中以前的值,将该值赋给变量A。从而实现了变量A和变量B中值的交换问题,这里没有使用任何第三变量。如果读者还有疑问的话,可任选变量A、B的具体值代入,看看结果是否正确。
再让我们看另一个例子。
〔例2〕 不允许使用条件判断(IF…THEN…)语句,编一程序,输出变量A和变量B的两个值中较大的值。
刚读完题目,似乎不知道该怎样下手解题,既然不允许使用条件判断语句,又怎样知道变量A和变量B中的值哪一个更大一些呢?不知道哪个变量的值更大,又如何输出较大的值呢?这个思路似乎很有道理,但题目只要求输出变量A和变量B的其中一个较大的值,并未要求判断哪个变量的值更大一些,所以应该有的放矢。采用一些技巧就能解决此问题,用程序表达如下(其中,ABS是绝对值函数):
10 INPUT A,B
20 PRINT (ABS(A-B)+A+B)/2
30 END
让我们看一下程序中的表达式(ABS(A-B)+A+B)/2。当A≥B时,(ABS(A-B)+A+B)/2=(A-B+A+B)/2=A;当A<B时,(ABS(A-B)+A+B)/2=(B-A+A+B)/2=B。可见,无论变量A和变量B中的值哪一个大,表达式(ABS(A-B)+A+B)/2均给出较大的变量值。上程序仅用了这一小小的技巧便解决了这个问题。
再让我们看一个例子。〔例3〕有两个程序:程序1和程序2,如下所列:
程序1
10 FOR I=1 TO 10
20 M=RND(3)
30 IF M>=0.5 THEN M=1
40 IF M<0.5 THEN M=0
50 PRINT M;
60 NEXT I
程序2
10 FOR I=1 TO 10
20 M=RND(3)
30 M=INT(M+0.5)
40 PRINT M;
50 NEXT I
这两个程序做同样的事情——随机输出一列10个0、1代码。但哪一个程序写得更好些呢?比较一下这两个程序,可以看出,程序2中的语句30实现了程序1中语句30和语句40两条语句的功能。语句20M=RND(3)将随机产生的一个0~1之间的随机数赋给变量M,在程序1中用了两条条件判断语句对变量M的值四舍五入;在程序2中则仅用了一条赋值语句M=INT(M+0.5)来对变量M的值四舍五入。显然,程序2比程序1的技巧性要强,也显得简洁。(蒙濛)