(杨百一)一般的固定电阻器只有两根引线,如果将两个或更多个电阻器一个接一个地顺序串接起来,最后的两根引线再接电源,就构成电阻串联电路。图1是三个电阻串联的实物图,图2是对应的电路图。
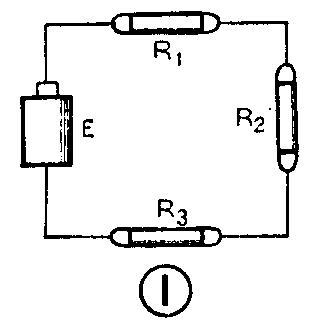
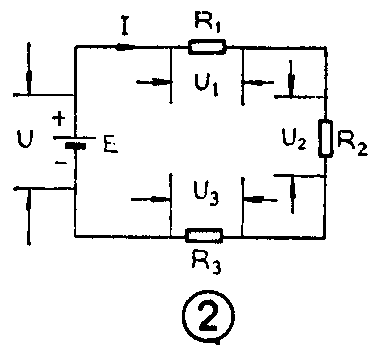
电阻串联电路及其特点
这种电阻串联电路有几个显著特点:
(l)流过电路中的电流处处相等。即流过电阻R\(_{1}\)、R2、R\(_{3}\)上的电流大小一样。这是因为,串联电路只有一条电流道路,电流从电池的正极流出,顺序流过R1、R\(_{2}\)、R3、三个电阻,最后流回到电流的负极,中途既不会减少,也不会增加。若用电流表测一下,无论在串联电路的何处测量,测得的电流都是一样大小。
(2)电路的总电阻等于各电阻之和。对图2电路来说,R\(_{总}\)=R1+R\(_{2}\)+R3。这是因为电流在流动过程中,要分别受到每个电阻的阻力,所以电路中总的阻力就等于各电阻的阻力之和。
(3)电路两端的总电压等于各电阻两端电压之和。电流流过电阻时,这个电阻两端的电压值就等于电流乘电阻,即U=I·R。因为在串联电路中,电流处处相等,所以各电阻两端电压之和为:U=U\(_{1}\)+U2+U\(_{3}\)=IR1+IR\(_{2}\)+IR3=I(R\(_{1}\)+R2+R\(_{3}\))。由这个算式可以看出,计算串联电路的总电压时,可先求出总电阻值,然后乘以电流值即可得总电压值。还可看出,由于流过各电阻的电流相等。所以各电阻上的电压大小主要由电阻值的大小决定,阻值大的,它两端的电压也大,阻值小的,电压也小。
(4)电路消耗的总功率等于各电阻消耗的功率之和,即P=P\(_{1}\)+P2+P\(_{3}\)。电流顺序流过各个电阻时,先后克服各个电阻的阻力而多次消耗功率,把在每个电阻上消耗的功率相加,就是整个串联电路消耗的总功率。计算式可表示为:
P=IU=I(U\(_{1}\)+U2+U\(_{3}\))=IU1+IU\(_{2}\)+IU3=P\(_{1}\)+P2+P\(_{3}\)
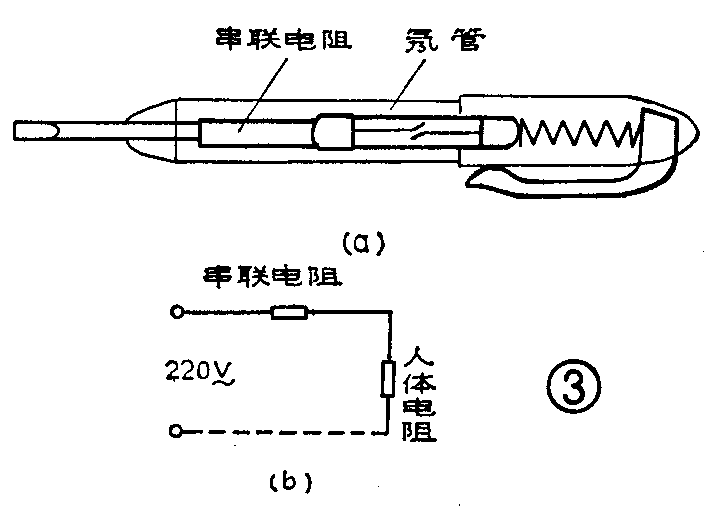
电阻串联电路的实用例子很多,例如:在我们日常使用的试电笔中,就串联了一个阻值很大的电阻,以保证使用安全。试电笔的构造如图3a所示。使用时,笔尖触及220伏电源火线,在这个电压作用下,氖管里的两电极之间发生辉光放电,出现一个亮点。如果不串入这个电阻,一旦人体与大地之间绝缘不好,人体的电阻不大,会有很大的电流通过人体,造成触电事故。串入这个电阻之后,如图3b所示,由于它的阻值很大(几十兆欧),流过人体的电流非常小,就不会发生触电事故。
例如在自装收音机时,为了调整晶体管的工作点,可用一个电位器与一个电阻串联后代替电路中带星号的电阻。调整好以后,量出串联后的总阻值,再找一个阻值与此相符的电阻焊上去即可。若手头没有合适的电阻,也可用两个或三个电阻串联起来代替。
电阻并联电路及其特点
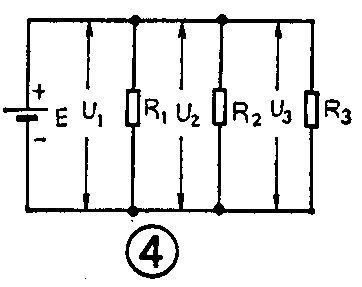
将两个或更多个电阻器的两端分别接在一起,然后在两端接上电源,就构成电阻的并联电路,如图4所示,由图中看出,三个电阻的上端接在一起,下端也接在一起,然后接电源E。对电源而言,每个电阻形成一条支路。
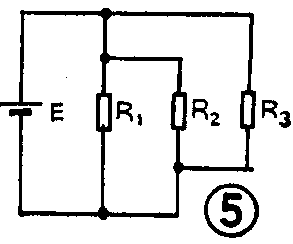
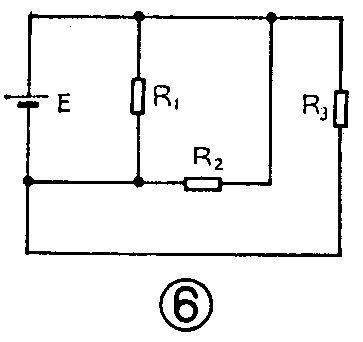
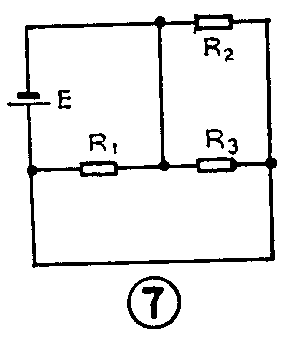
初学者在观察电路板时应特别注意,相并联的各个电阻的一端,既可以是直接将引脚焊在一起,也可以是通过导线把各电阻的引脚连到一起。同样在看电路图时,不管图中画出的连线有多长或怎样拐弯,只要各电阻的两端,能通过连线分别接到一起,那么这几个电阻就是并联关系。如图5、6、7中的电阻都是并联关系,因而这几个电路都是电阻并联电路。
电阻并联电路的特点
(1)各电阻两端的电压相等,并等于外加电源电压。如图4中,U\(_{1}\)=U2=U\(_{3}\)=E。
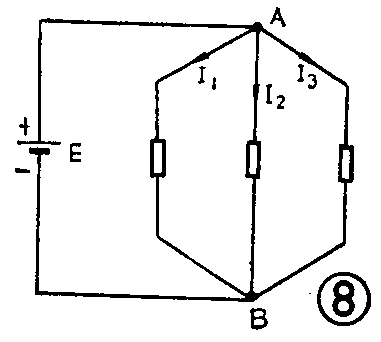
(2)各支路的电流加起来等于电源供给的总电流。我们将图4电路改画成图8,可知总电流I流过A点后,则兵分三路,变成I\(_{1}\)、I2,I\(_{3}\)三股电流,分别从三条支路通过。到达B点后,三个支路电流又重新汇合成总电流。因此,总电流就等于各支路电流之和:I=I1+I\(_{2}\)+I3。由于三股电流是由总电流中分配出来,如果三个并联电阻相等,则三股电流平均分配,大小相等,即I\(_{1}\)=I2=I\(_{3}\)。但是,如果三个并联电阻大小不同,那么三个支路上的电流将怎样分配呢?由欧姆定律I=U/R可知,在电压相同的情况下,支路电流与支路电阻成反比,即支路电阻大的分配的电流就小;支路电阻小的,分配的电流就大。
(3)并联电路中总电阻的倒数等于各支路电阻倒数的和,即\(\frac{1}{R}\)=1;R\(_{1}\)+\(\frac{1}{R}\)2+1;R\(_{3}\)。今后我们可能经常碰到计算并联电路总电阻的问题。如果用上述公式计算,显然是太繁杂了,必须找出一种简便方法,我们先看图9所示电路,这是一个只有两个电阻与电源相并联的电路。R1与R\(_{2}\)并联后的总电阻是多少呢?由\(\frac{1}{R}\)=1;R1+\(\frac{1}{R}\)\(_{2}\)可得R=R1·R\(_{2}\);R1+R\(_{2}\)。这就是今后要经常使用的一个计算并联电阻的公式,必须牢牢地记住。
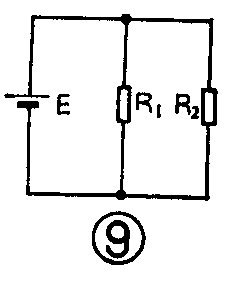
只有两个电阻并联时,可用上述简单公式算出总电阻。如果有三个以上电阻并联,我们可先将其中两个电阻并联后的阻值算出来,再将计算结果看作一个电阻,与第三个电阻并联进行计算。如此继续计算下去,就可将全部电阻并联的总电阻计算出来。
(4)电路中消耗的总功率于各电阻消耗功率的总和。如图4电路中P=P\(_{1}\)+P2+P\(_{3}\)。
这个结论与串联电路是一致的,但计算时各有特点。对于串联电路,主要抓住各处电流相等这个特点;对于并联电路,则主要利用各支路两端电压相等这个特点。
下面我们出几道思考题,请您做一下。
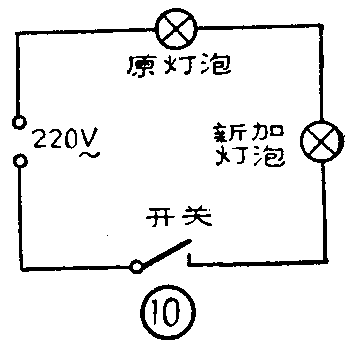
(1)小李房间里原有一盏25瓦的灯泡,他嫌亮度不够,又找来一个25瓦的灯泡,按图10所示电路接好,结果合上开关后反而更暗了。这是为什么?请算出两个灯泡共消耗多少功率?
(2)国庆节前厂长叫小张负责给厂大门口安装一些彩灯。已知买来的彩灯工作电压为10伏。工作电流为0.1安培。使用的电源是220伏市电。请帮小张想想,彩灯应如何连接?最少要用多少个彩灯?每个彩灯的电阻是多少?接好开灯后,全部彩灯消耗多少功率?
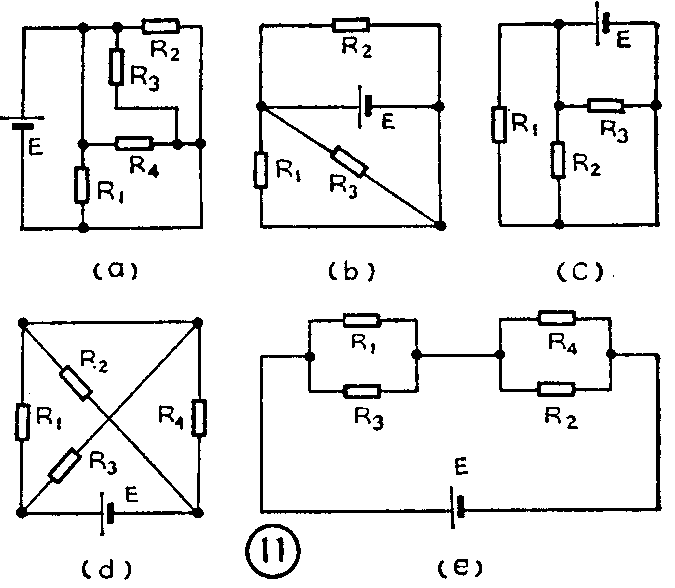
(3)图11(a)(b)(c)(d)所示电路中,哪些是电阻并联电路?哪些是既有并联又有串联的“混联”电路?
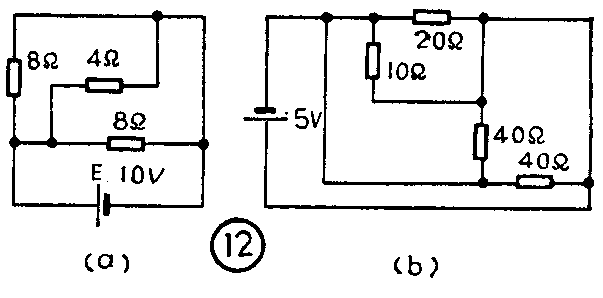
(4)计算图12(a)(b)电路中的总电阻各为多少?总电流各为多少?
思考题答案:
(1)由图10可以看出,两个灯泡是串联接入电源的。串联后,总电阻增加一倍,电压没变,则流过两灯泡的电流减小一半,所以两个灯泡都变暗了。设每个灯泡的电阻为R。只接一个灯泡时消耗的功率为:P\(_{1}\)=\(\frac{U}{^{2}}\)R,可推出R=U2;P1。两个灯泡串联后消耗的总功率为:P\(_{2}\)=\(\frac{U}{^{2}}\)2R=U2;2\(\frac{U}{^{2}}\)P1=P\(_{1}\);2=12.5(瓦)可见多串联一个灯泡以后,消耗的总功率反而减小了一半,每个灯泡消耗的功率只有原来的四分之一。所以说,用多串灯泡的方法不能增加亮度,正确的方法应并联。
(2)因为每个彩灯的工作电压是10伏,而电源电压是220伏,所以应采用串联的办法,把许多个彩灯串接起来,使总的工作电压正好为220伏,这样,就可算出共需要多少个彩灯:\(\frac{220}{10}\)=22(个),即共需22个彩灯。设每个彩灯的电阻力P,则R=U;I=10伏0.1安=100欧
全部彩灯消耗的总功率为每个彩灯消耗功率的22倍,即P=22×P\(_{0}\)=22×U×I=22×10×0.1=22(瓦)
(3)图11(a)(b)(c)电路均为电阻并联电路。图d是既有并联又有率联的“混联电路”。我们在看电路图时,只要是用实线相连,不管连线多长,连线如何拐弯,都可认为是接在一起。根据这个道理,将图d改画成下图e,可见R\(_{1}\)与R3、R\(_{4}\)与R2分别相并联,然后两个并联电路又串联。
(4)图12(a)(b)都是电阻并联电路。计算有三个以上电阻相并联的总电阻时,可先算出其中两个电阻并联后的“等效电阻”,再将计算结果与第三个电阻相并联继续计算,就可算出全部电阻并联后的总电阻。例如,对图a电路,可先算两个8欧电阻并联后的阻值为:
R=\(\frac{8×8}{8+8}\)=64;16=4(欧),
再用算出的结果(4Ω)与图中4Ω电阻相并,算出总电阻为:
R\(_{总}\)=\(\frac{4×4}{4+4}\)=16;8=2(Ω)
总电流I=\(\frac{U}{R}\)=10;2=5(A)
对图b电路,可先算两个40欧电阻相并联的阻值,再算与20Ω电阻相并联的阻值,最后算与10Ω电阻相并联的总阻值:
两个40Ω电阻相并联:R\(_{1}\)=\(\frac{40×40}{40+40}\)=20(Ω)
再与20Ω电阻相并联:R\(_{2}\)=\(\frac{20×20}{20+20}\)=10(Ω)
最后与10Ω电阻相并联的总阻值
R\(_{总}\)=\(\frac{10×10}{10+10}\)=5(Ω)
总电流为I=\(\frac{U}{R总}\)=5伏;5欧=1(安)