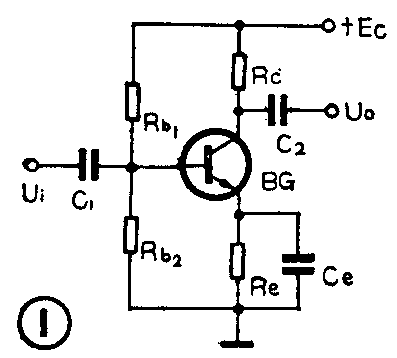
1.在一般的低频放大器中(见图1),发射极电阻R\(_{e}\)两端并联的电容取值较大,约为几十微法。但有些电路,Ce取值很小,只有几十至几百皮法。想想看这是什么原因?
2.为什么TTL电路的输入端在悬空时可视为输入高电平“I”,而CMOS电路的输入端却不允许悬空。
3.两种复合管电路如图3(a)、图3(b)所示。你能说出它们在性能上有何异同吗?
想想看答案
1.在一般的低频放大电路中,C\(_{e}\)取得较大是为了使它能对Re有良好的旁路作用,以防止因R\(_{e}\)引起负反馈而使电路的放大倍数降低。有的电路Ce取值较小,是为了用它来补偿电路的高频响应。其原理是:信号的频率越高,C\(_{e}\)与Re的并联阻抗越小,电路中的负反馈也就越弱,于是电路的放大倍数得到提高,从而可补偿高频段的频率响应。
若在并联C\(_{e}\)前已知电路的高频截止频率为fH,只要选择C\(_{e}\)使Ce=1/2πf\(_{H}\)Re,便可将f\(_{H}\)提高。Re越大,f\(_{H}\)提高得也越多,从而改善了电路的高频特性。但是,这样作在中频段由于Re的反馈作用,会使电路的放大倍数降低,因而这里高频特性的改善是以牺牲中频段的放大倍数为代价的。
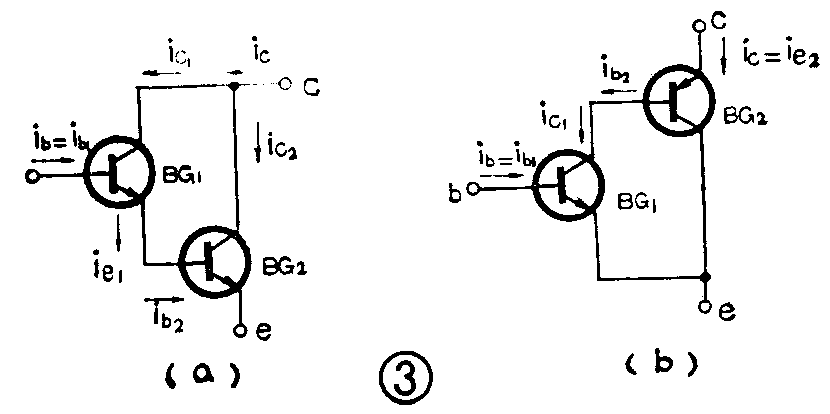
2.当TTL电路的输入端与地之间接入一电阻R时,就会有输入电流I\(_{i}\)流经R并在R上产生电压UR,见图2。当R的阻值很小时,U\(_{R}\)也很小,TTL电路相当输入一个低电平,即输入为O。当输入对地短路(即R=O)时,就是理想的O电平输入。反之,R的阻值越大,UR就越高,当高于TTL电路的开门电平时,就相当于有一个高电平接在输入端,即相当于输入为“I”。若输入端悬空,相对于R→∞,这时U\(_{R}\)最高,当然可视为输入高电平“1”。而CMOS电路的输入端是MOS场效应管的栅极,若是悬空,将与分立元件中的MOS场效应管一样,极易产生较高的感应电压而使电路损坏,即使在输入端设有保护装置电路不使电路损坏,也会因电路的输入阻抗很高而引起感应电压破坏电路的正常工作,所以CMOS电路的输入端是不允许悬空的。
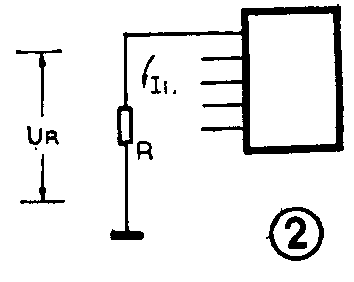
3.图3(a)电路是由两只NPN型三极管构成的复合管,图3(b)则是由一只NPN型三极管和一只PNP型三极管构成的复合管。它们在性能上的相同点是:
(1)都相当于一只NPN型三极管。
(2)电流放大倍数都很大。对图(a)来说,有:
i\(_{C}\)=iC1+i\(_{C2}\)=β1ib1+β\(_{2ib2}\)=β1ib+β\(_{2ie2}\)=β1ib+β\(_{2}\)(1+β1)\(_{ib1}\)=β1ib+β\(_{2}\)(1+β1)\(_{ib}\)。
β=i\(_{c}\)/ib=β\(_{1}\)+β2+β\(_{1}\)β2≈β\(_{1}\)β2。
对图(b)则有:
i\(_{c}\)=ie2=(1+β\(_{2}\))ib2=(1+β\(_{2}\))ic1=(1+β\(_{2}\))β1
i\(_{b1}\)=(1+β2)β\(_{1ib}\)
β=i\(_{c}\)/ib=β\(_{1}\)+β1β\(_{2}\)≈β1β\(_{2}\)
即它们的共发射极电流放大倍数,都约等于两只三极管共发射极电流放大倍数β\(_{1}\)和β2的乘积。
(3)穿透电流I\(_{CEO}\)都较单只三极管大。这是由于在复合管的穿透电流中,除含有BG2的穿透电流I\(_{CEO2}\)外,还含有BG1的穿透电流I\(_{CEO1}\)经BG2放大后产生的电流。故复合管的穿透电流I\(_{CEO}\)为:
I\(_{CEO}\)=(1+β2)I\(_{CEO1}\)+ICEO2
它们在性能上的不同点是
(1)图(a)电路的导通电压U\(_{BET}\)比图(b)电路高。若BG1、BG\(_{2}\)的导通电压分别为UBET1、U\(_{BET2}\),则图(a)电路的导通电压UBET=U\(_{BET1}\)+UBET2。图(b)电路的导通电压U\(_{BET}\)=UBET1
(2)图(a)电路的输入电阻r\(_{be}\)比图(b)电路大。
对图(6)有:
r\(_{be}\)=Ubei\(_{b}\)=Ube1+U\(_{be2}\);ib1=\(\frac{i}{_{b1}}\)rbe1+i\(_{b2}\)rbe2i\(_{b1}\)
=\(\frac{i}{_{b1}}\)rbe1i\(_{b1}\)+(1+βi)i\(_{b1}\)rbe2;i\(_{b1}\)=rbe1+(1+β\(_{1}\))rbe2
对图(b)则有:
r\(_{be}\)=Ubei\(_{b}\)=Ube1;i\(_{b1}\)=ib1r\(_{be1}\)ib1=r\(_{be1}\)
(吴明)