石英晶体的正式学名叫石英谐振器,有时简称晶体(CRYSTAL)。它是一种频率控制器件,在电子设备中,凡是需要精确控制频率的场合,石英晶体往往是不可缺少的。
石英晶体通常有两根引线。在不加激励的情况下,在两引线之间可测量出电容量,这个电容叫做静电容C\(_{0}\)。若在两引线之间加上适当的激励电压,石英晶体将产生机械振动,这时可把石英晶体看作是一个由电感L1、电容C\(_{1}\)、电阻R1和静电容C\(_{0}\)组成的谐振电路,其等效电路如图1a所示。石英晶体在电路图中的符号见图1(b)。
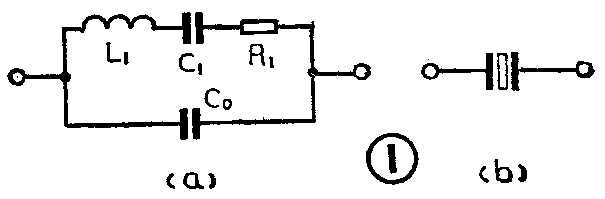
通常,把石英晶体等效电路中的C\(_{0}\)支路叫做静态支路,而把L1、C\(_{1}\)、R1支路叫做动态支路。一个石英晶体在静态(不振动)时,仅呈现为静电容C\(_{0}\);只是在动态(振动)时,才呈现为图1所示的等效电路。L1、C\(_{1}\)和R1分别叫做等效动态电感、等效动态电容和等效动态电阻。L\(_{1}\)和C1反映了石英晶体振动时的频率特性,R\(_{1}\)则反映了石英晶体振动时的机械损耗。
从电路分析可以知道,当L\(_{1}\)—C1—R\(_{1}\)支路谐振时,可形成串联谐振,其串联谐振频率为
f\(_{s}\)=\(\frac{1}{2π}\)\(\sqrt{L}\)1C\(_{1}\) (1)
当L\(_{1}\)—C1—R\(_{1}\)支路与C0支路组成并联谐振电路时,其并联谐振频率为
f\(_{p}\)=\(\frac{1}{2π}\)\(\sqrt{L}\)1(1/C\(_{1}\)+1/C0)≈f\(_{s}\)(1+C1;2C\(_{0}\)) (2)
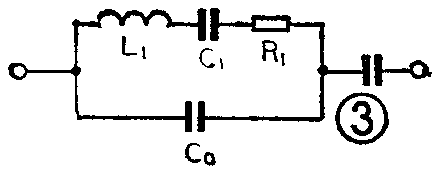
由于任何产品的参数都具有一定的离散性,石英晶体的f\(_{s}\)和fp也有较大的离散性,很难找到两只晶体使它们的f\(_{s}\)和fp完全相同。所以,在实际应用中,石英晶体既不工作在f\(_{s}\),也不工作在fp,而是工作在f\(_{s}\)和fp之间的某一工作频率f上。为此,必须像图2那样和石英晶体并联一只电容C\(_{L}\);或者像图3那样和石英晶体串联一只电容CL。这个C\(_{L}\)就叫做石英晶体的负载电容。CL往往做成可调的,以便通过调整C\(_{L}\)。使石英晶体的实际工作频率f等于预先设计的标称频率fn。
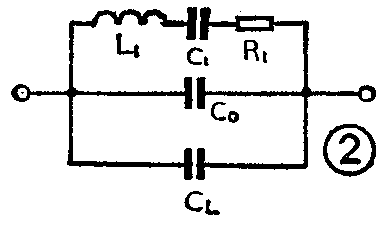
对于图2电路,相当于把石英晶体等效电路中静态支路的电容C\(_{0}\)增加为C0+C\(_{L}\),因此该电路的并联谐振频率应为
f'\(_{p}\)=\(\frac{1}{2π}\)\(\sqrt{L}\)1C\(_{1}\)(C0+C\(_{L}\));C1+C\(_{0}\)+CL
≈f\(_{s}\)[1+C12(C\(_{0}\)+CL)(3)
对于图3电路,应用两端网络理论可证明其串联谐振频率为
f'\(_{s}\)=fs\(\sqrt{1}\)+\(\frac{C}{_{1}}\)C0+C\(_{L}\)≈fs[1+C\(_{1}\);2(C0+C\(_{L}\))] (4)
比较公式(3)和(4),即可知道,图2和图3中,石英晶体的工作频率是相等的。即
f=f'\(_{s}\)=f'p=f\(_{s}\)[1+C12(C\(_{0}\)+CL)] (5)
从以上分析可知,石英晶体的实际工作频率f,除了取决于其本身的技术参数(f\(_{s}\)和fp)外,还取决于和它相连接的负载电容C\(_{L}\)的大小。从公式(5)看出,当CL从∞变化到0时,f将从f\(_{s}\)变化到fp(在实际应用中,一般是使f靠近f\(_{s}\))。因此,对于生产者或使用者来说,石英晶体的负载电容CL都是一个很重要的技术条件。
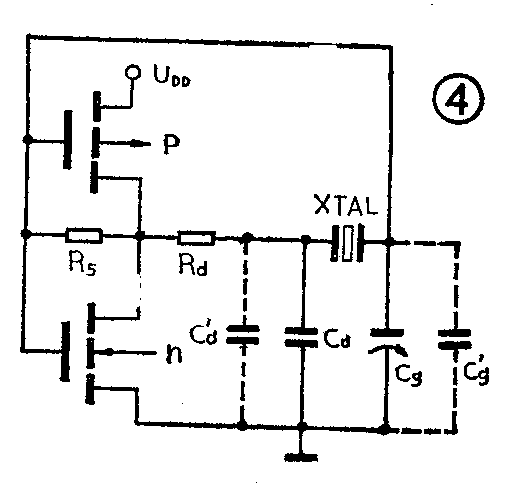
例如图4所示的石英电子手表晶体振荡电路中,晶体XTAL的负载电容C\(_{L}\)=CdC\(_{g}\)Cd+C\(_{g}\),它是采用图2的形式,和晶体并联而成的。Cd是固定电容,C\(_{g}\)是微调电容。调节Cg就能改变C\(_{L}\)的大小,从而能使手表晶体的工作频率f准确地调整到标称频率fn(f\(_{n}\)=32768Hz)。
设某手表用石英晶体的等效动态电容C\(_{1}\)=3×10\(^{-}\)3pF(微微法),等效动态电感L=7865.3H(亨利),静电容C0=1.5pF。代入公式(1)和(2),即可计算出晶体的串联谐振频率f\(_{s}\)=32764.37Hz,并联谐振频率fp=32797.13Hz。当负载电容C\(_{L}\)=12pF时,依公式(5)可计算出该晶体的工作频率为32768Hz。
如果实际电路中采用的C\(_{d}\)=39pF,Cg=5~35pF,则负载电容的可调范围为C\(_{L}\)=4.43~18.45pF。当CL为最大值时,晶体的最低工作频率fmin=32766.83Hz;当C\(_{L}\)为最小值时,晶体的最高工作频率fmax=32772.66Hz。
一般手表用石英晶体的负载电容C\(_{L}\)多为数微微法至数十微微法。晶体制造厂必须根据用户提出的CL值,计算出f\(_{s}\)和fp应有的值,作为设计和制作晶体的依据,才能使晶振电路调整到标称工作频率上。
在低档数字表中,为了降低成本,一般都省去了C\(_{d}\)和Cg,这时就要靠CMOS倒向器的输入电容C\(_{g}\)和输出电容C'd构成负载电容C'\(_{L}\)=C'aC'\(_{g}\)C'd+C'\(_{g}\)和晶体并联。通常由于C'L小于手表晶体的C\(_{L}\),所以低档数字表走时一般都偏快。从以上的讨论可知,对于走时偏快的低档数字表,可以在Cd或C\(_{g}\)的两端并联适当容量的小电容;而对于走时偏慢的低档数字表,可以在Ca—晶体—C\(_{g}\)回路中串联一只适当容量的小电容,以提高晶体的工作频率。不过由于可供调节的范围不大,并不是所有的低档数字表都能调整得分秒不差,这时就必须更换合适的手表晶体才能解决问题。
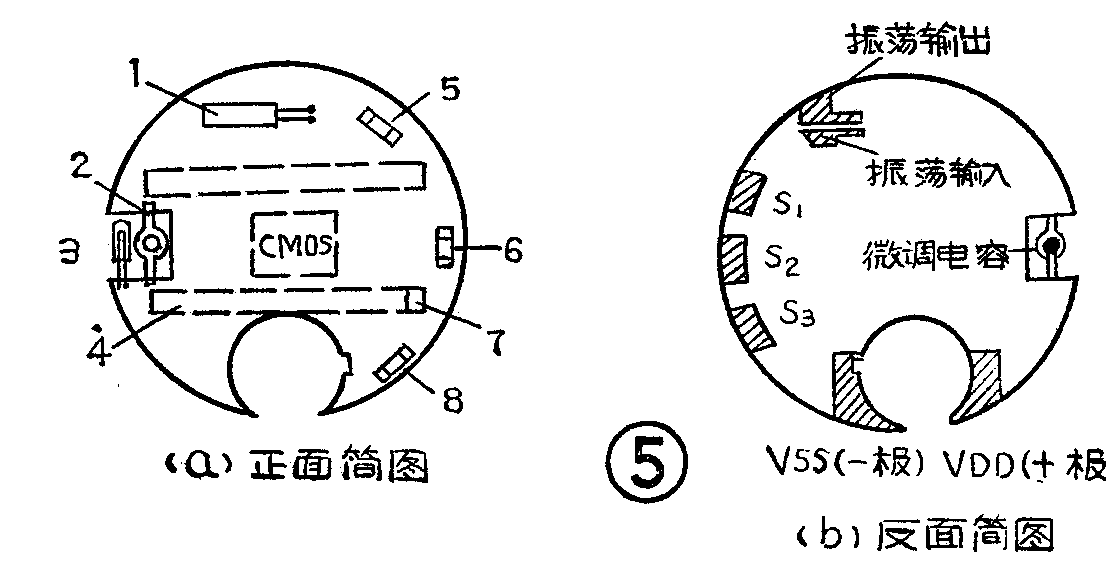
在了解了石英晶体负载电容、等效电路、手表用石英晶体工作频率的计算及调整之后,为了使读者对数字式石英电子表有所了解,这里给出一般数字式石英电子表的结构简图,见图5。图5(a)为正面简图,图5(b)为反面简图。在图5(a)中,标有数字1、2、3……8,其中,1.为石英谐振器,2.为微调电容C\(_{g}\),3.为照明小灯泡,4.为导电橡胶,5.为固定电容Cd,6、8为升压电容,7.为液晶显示器公共电极。(蒋伟)