计算机中的用的是二进制数。它与我们常用的十进制数不同,二进制数只用两个数码0和1表示;十进制数“逢十进一”,二进制数则是“逢二进一。”计算机为什么用二进制数呢?这是由于计算机是由逻辑电路组成,逻辑电路只有两个状态——高电平和低电平,恰好用高电平表示1,低电平表示0。二进制比十进制更简单,但由于习惯,人们对二进制数反而不如对十进数熟悉。
每个十进制数都可以写成多项式形式,如12.625可以表示为1×10\(^{1}\)+2×100+6×10\(^{-}\)1+2×10-2+5×10\(^{-}\)3形式,同样,也可以把一个二进制数写成多项式形式,如:1101.101可以写成1×23+1×2\(^{2}\)+0×21+1×2\(^{0}\)+1×2-1+0×2\(^{-}\)2+1×2-3。
二进制数与十进制数的互相转换
在使用微电脑的过程种中经常用到二进制与十进制数的互相转换。这里介绍一下转换的方法。
二进制转换成十进制的过程很简单,如:把二进制数1101.101转换成十进制数可按如下方法:1101.101(二进制数)=1×2\(^{3}\)+1×22+0×2\(^{1}\)+1×20+1×2\(^{-}\)1+0×2-2+1×2\(^{-}\)3=8+4+1+0.5+0.125=13.625(十进制数)
从这个例题我们可以看出小数点前用的是正幂,小数点后面用的是负幂,幂的绝对值从0向正负两个方向依次增加。
十进制数转换成二进制数比较复杂。要把十进制数的整数部分与小数部分分别转换成二进制数的相应部分。
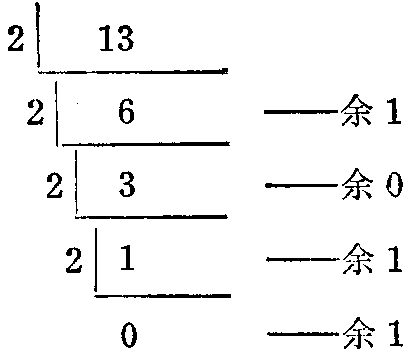
下面把十进制整数13转换成二进制数。假设二进制整数是B\(_{n}\)Bn-1……B\(_{1}\)B0,那么13=B\(_{n}\)·2n+B\(_{n}\)-1·2\(^{n}\)-1+1·2+B\(_{0}\)。从这个表达式可以看出,B0恰是13除以2的余数,B\(_{1}\)是得到的商数再次除以2的余数,以此类推。所以把13转换成二进制数的过程就是连续被2除求余数的过程,具体步骤是:把十进制数除以2并记下余数,所得的商再除以2,并记下余数如此不断继续下去直到商得0为止,即:
收集余数,从余数的末位开始写起,直写到余数的第一位为止,可以写出1101,结果得
13(十进制)=1101(二进制),或13\(_{1}\)0=110112
下角标在这里表示该数的进位制。
下面再看看小数部分如何转换。以0.625为例。假设转换成的二进制小数是:0.B\(_{-}\)1B-2\(_{-}\)m,则0.625=B-1·2\(^{-}\)1+B\(_{-}\)2·2-2-m·2\(^{-}\)m,将等式两边同时乘以2,B\(_{-}\)1正好是0.625乘以2之后的整数部分,B-2是0.625乘以2以后的小数部分再次乘以2的整数部分,以此类推直至B\(_{-}\)m。可以把这个步骤表示如下:
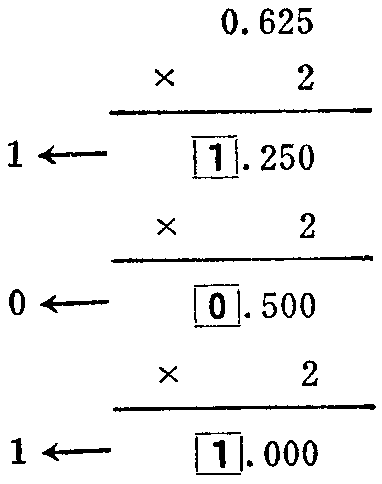
我们把小方框中的1和0叫“溢出”。结果是这样记录的将第一个溢中位作为二进制数小数点后的第一位;第二个溢出位作为小数点后的第二位;以后顺序与下去。从最高位到最低位与产生溢出的顺序是一致的。所以结果是(0.625)\(_{1}\)0=(0.101)2对0.625这个数,乘了三次2后小数部分就为0了,但有的数无论乘多少次2,小数部分也不为0,这不要紧,只要达到所要求的精度位数就行了。
二进制编码
虽然计算机采用二进制数运算,但计算机还要对字母、符号和十进制数进行处理,因此还要用二进制数表示,这就提出了二进制编码的问题。二进制编码有很多种,常用的字符符号编码是ASCII码(American Standard Code for Information Interchange美国信息交换标准代码)。它用7位二进制数表示128个字符。这种编码主要用于计算机与外围设备(如打印机、终端设备)或计算机之间的通讯。ASCII码已成为国际标准代码,我国也把它列为国标(美元符号$改成了人民币符号¥)。在ASCII码中,0000~0011111是功能码,它表示一定的功能,例如0001101表示回车,0001010表示换行符。从0100000到1111111则表示字符。例如0110000~0111001表示阿拉伯数字0~9,1000001~1011010表示英文26个大写字母而1100001~1111010表示26个小写字母。下边是美国信息交换标准码ASCII(七位代码)表。
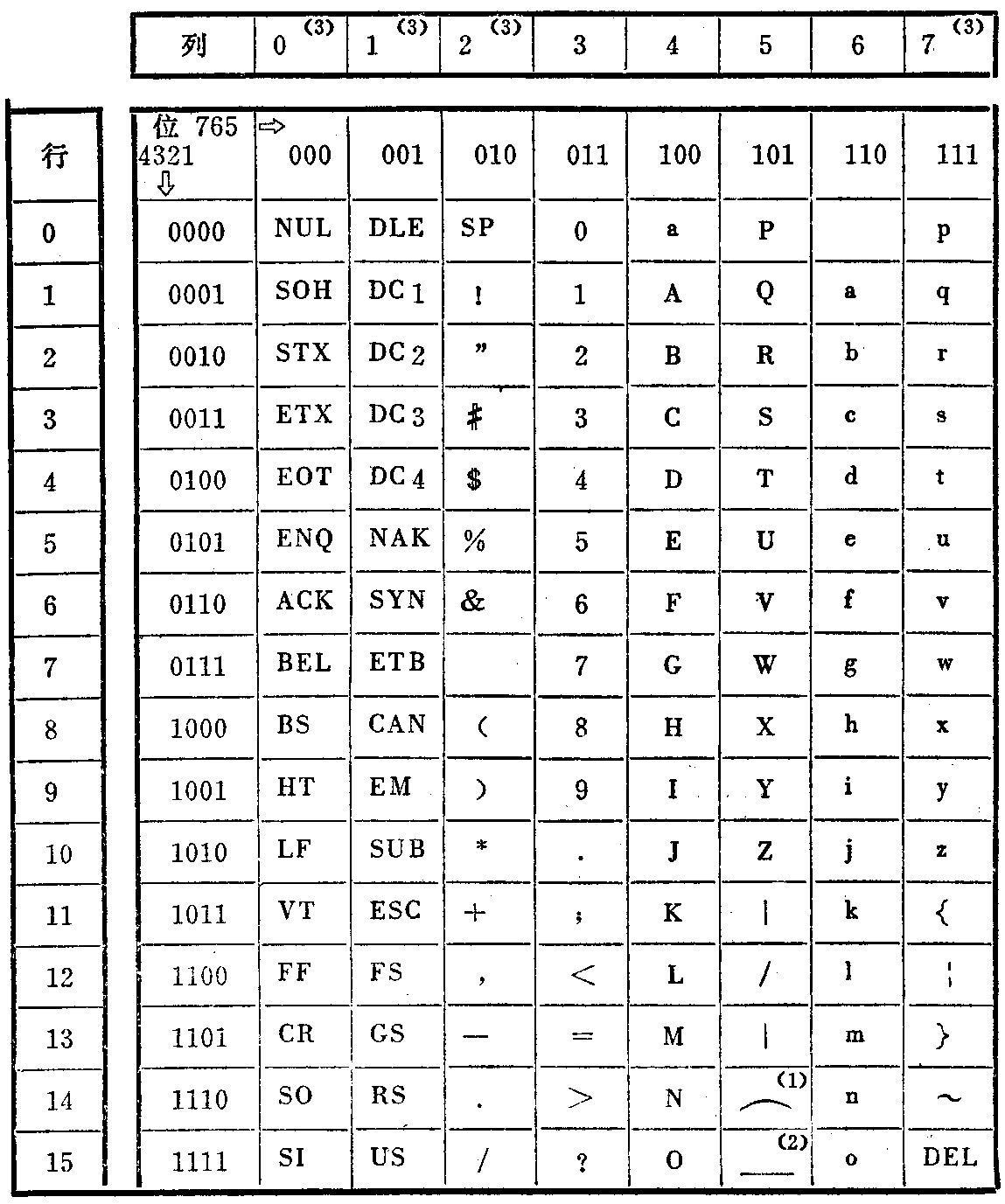
计算机中常用的另一种代码是BCD码(Binary Coded Decimal二进制编码的十进制数)。它是用四位二进制数表示10个十进制数字0~9。例如二进制的0000表示十进制的0,0111表示7。
BCD码比较直观,计算机使用它能够直接对十进制数进行运算。(张京城)