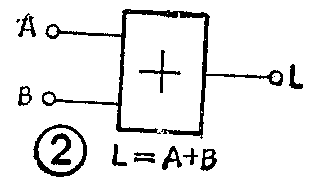逻辑代数浅谈

采用基本逻辑门组成各种逻辑电路，可以实现预定的逻辑功能。实际上，实现同一逻辑功能的电路，可以有多种不同的组成方式，有的简单，有的复杂，这就要求我们认识和掌握逻辑电路的规律，能够选择最为经济合理的方案，以达到既能实现预定的逻辑功能，又能使所用的逻辑门和连线最少。逻辑代数正是用来分析和研究逻辑电路的一种数学工具。

逻辑代数又叫布尔代数，人们利用它可以巧妙地进行数字系统的逻辑分析。学习数字电路，有必要掌握逻辑代数的基本运算法则和一些常用公式。

逻辑代数也和普通代数一样，用字母A、B、C…表示变量。但是，逻辑代数的变量只取两个值，即0和1，这里的0和1不是表示具体的数量大小，而是表示电路中两种对立的状态，如：信号的有、无，电位的高、低，开关的通、断等。显然，逻辑代数还需要有它特殊的运算规则。

本刊第一期介绍了“与”门、“或”门和“非”门三种基本逻辑门，它们的输出信号与输入信号之间的逻辑关系，可以用逻辑代数的三种基本运算来表示，这就是逻辑乘、逻辑加和逻辑非。

（1）逻辑乘

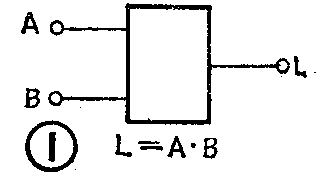
图1所示的“与”门，当输入端A与B都是高电平“1”时，输出L才是高电平“1”；如果输入端有一个最低电平“0”，输出L就是低电平“0”。这种逻辑关系如表1的真值表所示。

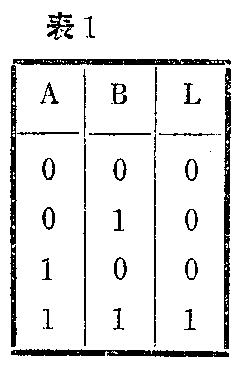
由真值表可见，输入信号A、B与输出信号L之间的关系，和一般算术运算中的乘法相同。在逻辑代数中，“与”逻辑可以用逻辑乘表示，即

对于多输入变量的“与”门，可写成

（2）逻辑加

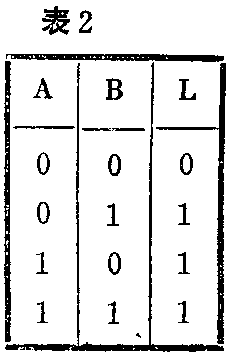
图2是大家熟悉的“或”门，它的真值表如表2所示。显然，输入信号A、B与输出信号L之间的关系，类似于普通的算术加法。因此，可用逻辑代数中的逻辑加来表示“或”逻辑，即

需要注意的是，这里有1＋1=1，而不是一般加法的1+1=2，也不是二进制加法的1＋1=10，这是逻辑加法的特殊规律。

（3）逻辑非（求反运算）

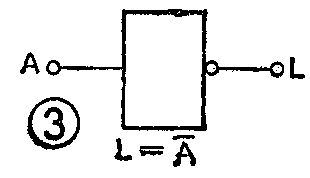
“非”门（图3）的输出信号L是输入信号A的反。即A=1，L=0；A=0，L=1。用逻辑代数式表示为

这种逻辑运算叫逻辑非或求反运算，A上的横线叫反演符号，这也是逻辑代数特有的一种运算。

大家知道，组成逻辑电路的除了上述的“与”门、“或”门及“非”门外，还有“与非”门、“或非”门及“与或非”门，等等。一个逻辑电路，往往有多个逻辑变量，输出信号与输入信号的关系是由多种门电路组合起来实现的。这种逻辑关系可以用一个逻辑函数来描述。下面举一个简单的实际例子。

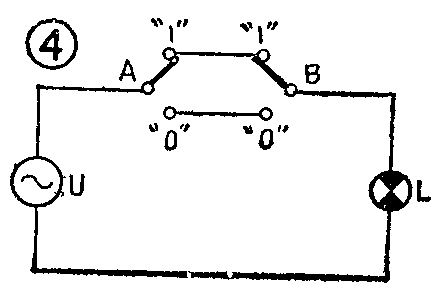
图4是一个两处共同控制一盏电灯的简单电路。A处和B处各装有一只双刀双掷开关，任何一处都可以控制电灯的点燃和熄灭。这里，我们取L=1表示灯亮，L=0表示灯灭。用1表示开关向上扳，用0表示开关向下扳。L与A、B的关系可列成表3所示的真值表。

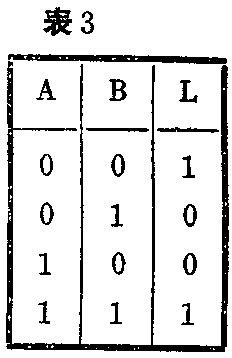
由真值表可见，在A、B状态的四种组合中，只有当A与B都是0或A与B都是1时，才能使灯亮（L=1）。这两种组合中A、B是“与”逻辑关系，可用逻辑乘表示，而两种组合之间又存在着“或”逻辑关系，可用逻辑加表示，写成逻辑代数式为

上式两个乘积项中，A·B表示A与B都是1，A--表示A与B都是0（即1的反）。

由上例可知，当A、B取一组值以后，L就有一个确定的值与它相对应，所以，L是A、B的函数。我们把L叫输出逻辑变量，A、B叫输入逻辑变量。真值表和逻辑代数式是逻辑函数的两种不同的表示方法。

掌握了逻辑代数的三种基本运算和逻辑函数的概念后，就可以把几种常见的门电路用逻辑函数式来表示。

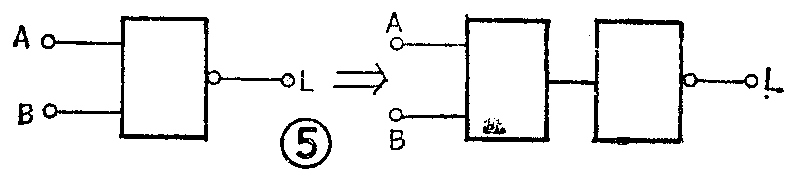
图5是“与非”门的逻辑符号，它是一个“与”门和一个“非”门的组合。我们可以用逻辑乘表示“与”逻辑，用逻辑非表示“非”逻辑。于是，“与非”门的逻辑式可写成

由真值表可见，输入信号A、B与输出信号L之间的关系，和一般算术运算中的乘法相同。在逻辑代数中，“与”逻辑可以用逻辑乘表示，即

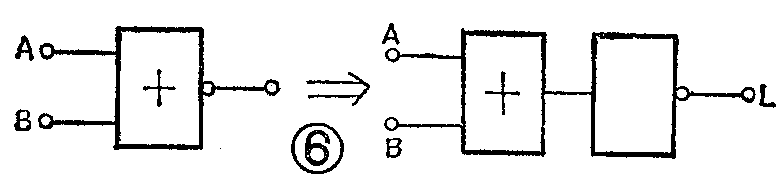
图6的“或非”门是一个“或”门和一个“非”门的组合，可以先后用逻辑加和逻辑非运算来表示，即

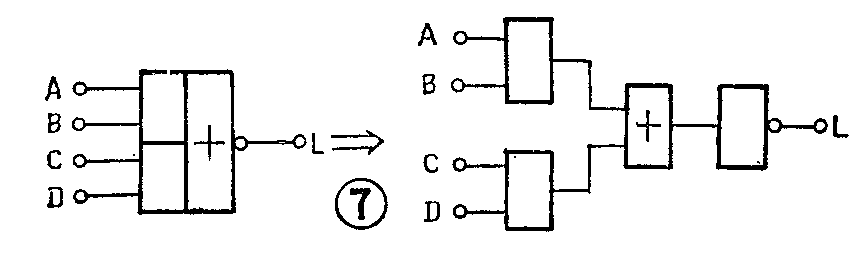
图7是一个“与或非”门，它是两个“与”门、一个“或”门及一个“非”门的组合，因此用逻辑乘、逻辑加和逻辑非运算来表达，即

“逻辑乘”、“逻辑加”、“逻辑非”是最基本的运算规则，是学习逻辑代数的入门知识。（张晋纯 宋东生 编译）