上一讲已经谈过,数字电路普遍采用二进计数制,但是数字设备的显示器却能显示出十进制数字,这是什么缘故呢?为了回答这个问题,本文简单谈谈有关译码和译码器的知识,介绍辉光数码管的译码与显示电路。
译码器是一种条件开关
我们已经讲过电子计数器的原理。计数器在进行累计计数时,是用“0’和“1”组成的一系列代码来代表0~9这十个十进制数字的。为了便于读取计数结果,显示器件(如数码管)必须用十进制数字直观显示。把二进制代码“翻译”成对应的十进制数的过程叫译码,实现译码功能的逻辑电路叫译码器。
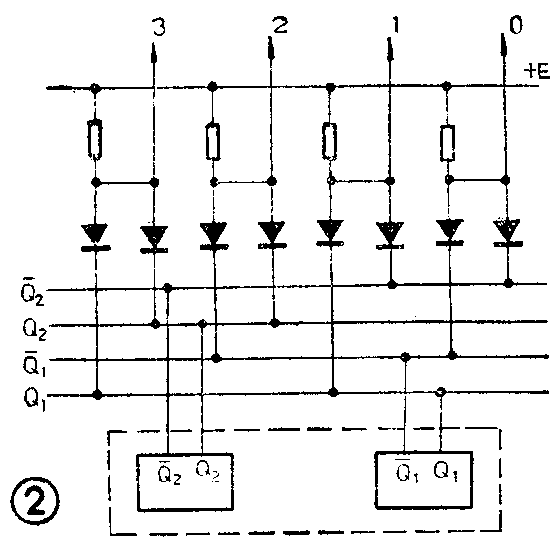
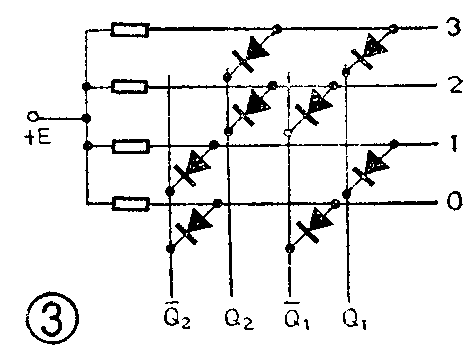
例如,一个两位二进制计数器,有“00”、“01”、“10”、“10”四组代码,分别代表0、1、2、3这四个十进制数字。对这种最简单的二进制代码进行译码,可以使用四个“与”门(图1),哪一个“与”门的输入信号组合满足“与”逻辑条件,这个“与”门就有信号输出,其余“与”门不满足开门条件,就没有信号输出。假定组成这个计数器的两个触发器输出状态为Q\(_{1}\)=1、Q2=0,则二进制代码是“01”,这时Q\(_{1}\)=1、Q-1=0;Q\(_{2}\)=0、Q-2=1,只有与门1的两个输入端(Q\(_{1}\)、Q-2)都是高电平“1”,它的输出线Z\(_{1}\)就有高电平信号输出。而其它三个与门的输入端都是至少有一个为低电平“0”,它们的输出端均为低电平“0”,所以相应的输出线上没有信号输出。这样,就把代码“01”判断和区别出来,输出线Z1上给出代表十进制数“1”的数字信号。其余类推。
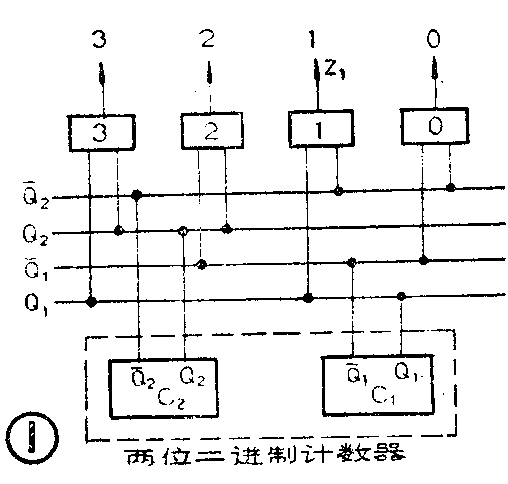
图4是采用集成电路与非门组成的译码电路。用与非门代替与门,输出还要加一级非门,但因集成电路与非门是最常用的一种门电路,而且一片电路中常包含4~6个与非门,所以用与非门电路组成译码器还是很方便的。
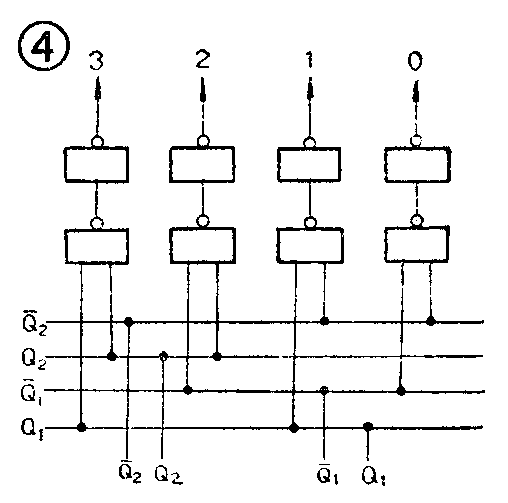
由此可见,译码器实际上是由门电路组成的“条件开关”。对每个门来说,输入信号的组合满足一定的条件时门就开启,输出线上就有信号输出;不满足给定条件门就关闭,没有信号输出。
常用的显示器件——辉光数码管
在数字设备中,十进制计数器给出的二进制代码经译码器译码后,驱动显示器件显示出对应的十进制数字,整个过程的方框图如图5所示。显示器件的种类很多,这里先介绍一种最简单的数字显示器件——辉光数码管。

辉光数码管是一种辉光放电管,玻璃外壳内充有惰性气体,依靠管内气体的辉光放电来显示数字,它的结构示意及外形如图6所示。管内有十个阴极K\(_{0}\)~K9和一个公共阳极A。这十个阴极分别用金属丝弯成0~9十个数字形状,它们互相重叠,而相邻两个字形之间又留有很小的绝缘间隙,装在管内的支架上,通过内引线将十个不同字样的阴极分别引到管脚上,阳极引到另一个管脚上.其管脚接线图和电路符号如图7所示。
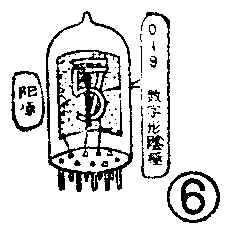
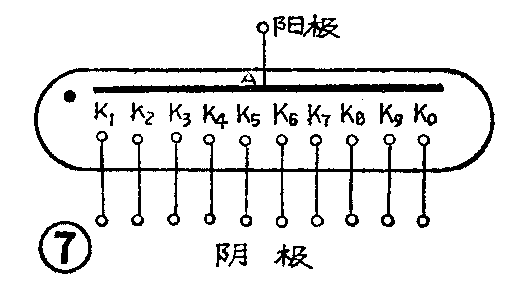
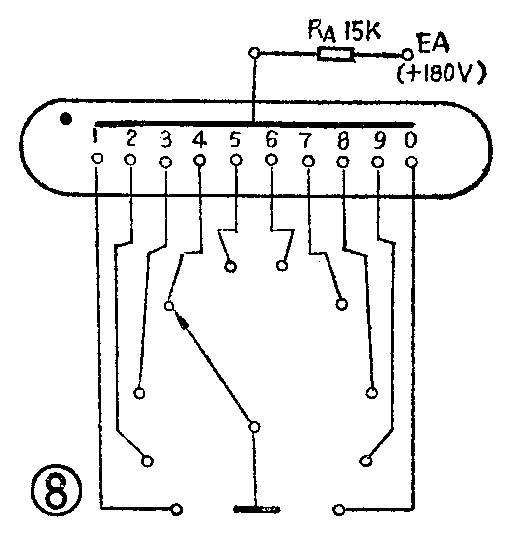
使用时阳极接有180伏的直流电压,当某一阴极为低电位(其余阴极悬空或处于高电位)时,则会在阳极和这个阴极之间产生辉光放电,这个阴极就显示桔红色悦目的辉光字形。图8是辉光数码管的显示实验电路。
译码显示电路原理
图9是采用辉光数码管的译码显示电路。在译码器的十条输出线和数码管的十个阴极引线之间接入十个晶体管作为驱动开关,数码管的每一个阴极由一个晶体管控制,每个管子的基极通过电阻R接到电源E上。十个晶体管的发射极分别和译码器的十个输出端相连。当需要显示某一个数字时,只要在相应晶体管的发射极施加低电平,则晶体管导通,相当于开关接通,对应的数字阴极就会发光显示。
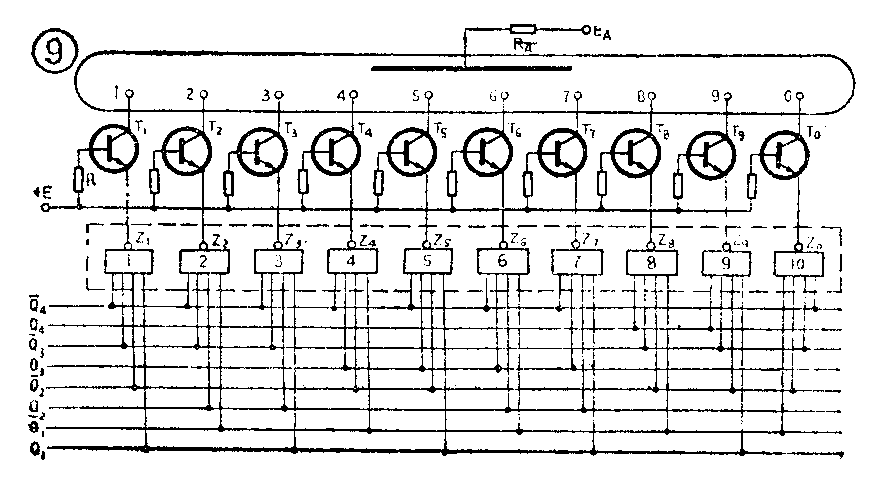
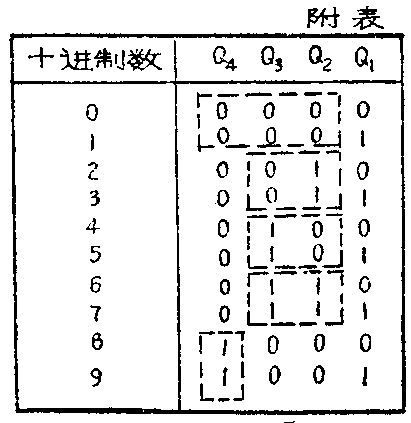
下面我们具体分析一下辉光数码管的译码电路。常用的十进制编码表如附表所示,组成计数器的四个触发器的Q\(_{4}\)Q3Q\(_{2}\)Q1端输出状态,就代表相应的十进制数的代码。例如,计数器的状态为Q\(_{4}\)=0、Q3=1、Q\(_{2}\)=1、Q1=0,代码就是“0110”,它代表十进制数“6”。用集成电路与非门进行译码时,我们取Q-\(_{4}\)Q3Q\(_{2}\)Q-1作为门6的输入信号,即Q-\(_{4}\)与Q3与Q\(_{2}\)与Q-1 都是高电平“1”时,输出为低电平“0”。用逻辑式表示为
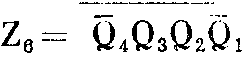
等式右边上方的横线是“非”逻辑符号,表示把Q-\(_{4}\)Q3Q\(_{2}\)Q-1再倒一次相,即Q-\(_{4}\)、Q3、Q\(_{2}\)、Q-1都为“l”时,译码电路的输出Z\(_{6}\)是它的反码“0”。
根据这个原则,我们可以把译码器十个输出端的逻辑表达式全部写出,即
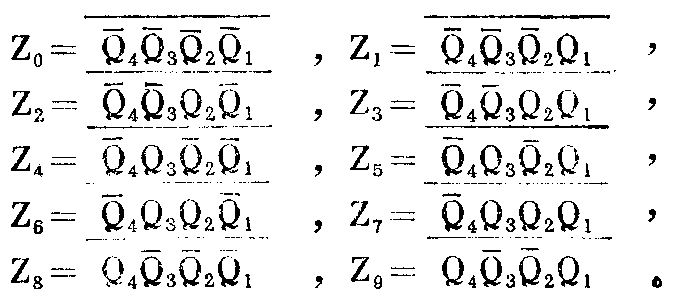
实用的辉光数码管译码器
图9所示的辉光数码管译码电路比较复杂,它一共用了十个与非门,而且每个与非门都需要四个输入端。实际上可以简化,下面介绍一种简化方案,只需五个与非门,并且与非门的输入端数也大为减少。
我们再来仔细看一看十进制计数器的编码表。由表可见,对十进制数中的偶数(0、2、4、6、8),Q\(_{1}\)端均为“0”,对奇数(1、3、5、7、9)则Q1端均为“1”。于是我们可以用Q-\(_{1}\)控制晶体管T0、T\(_{2}\)、T4、T\(_{6}\)、T8的基极,用Q\(_{1}\)控制晶体管T1、T\(_{3}\)、T5、T\(_{7}\)、T9的基极。这样,当Q-\(_{1}\)为低电平时,T0、T\(_{2}\)、T4、T\(_{6}\)、T8不可能导通,只有T\(_{1}\)、T3、T\(_{5}\)、T7、T\(_{9}\)可能导通,到底哪一个导通,就要看哪一个管的发射极为低电平了。
再看十个代码中的另外三位Q\(_{4}\)、Q3、Q\(_{2}\)各有什么特点。由附表可见,Q4=1时只有出现十进制数8和9两种可能,而且由于T\(_{8}\)、T9的基极已经用Q-\(_{1}\)、Q1加以控制,因此可用Q\(_{4}\)=1把8和9从0~9中区别出来。十进制数2~7虽然都是Q4=0,但Q\(_{2}\)、Q3的状态却有“01”、“10”、“11”三种状态,同理也可将它们分别区别出来:2和3的代码中都含有Q-\(_{3}\)Q2,4和5的代码中都含有Q\(_{3}\)Q-2,6和7的代码中都含有Q\(_{3}\)Q2。十进制数0和1却必须用Q-\(_{4}\)Q-3Q-\(_{2}\)三位代码才能把它们从其余各数中区分出来。这样,就可以把从0到9这十个数的代码分成五组,用五个与非门译码,它们的逻辑表达式为
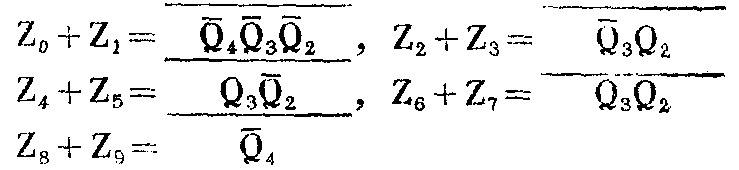
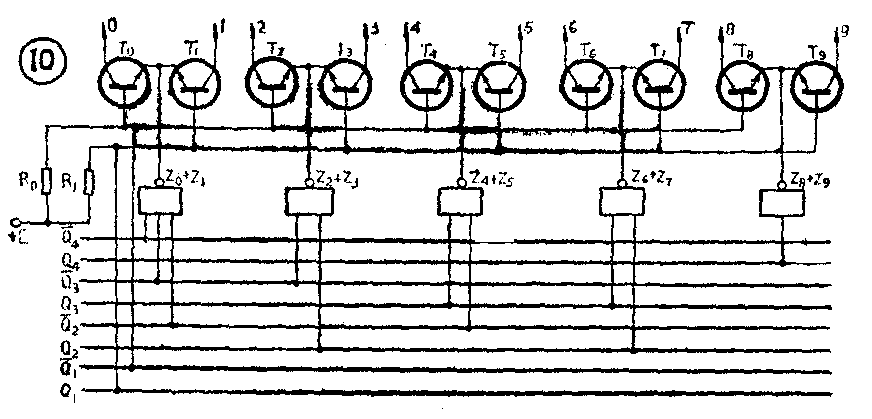
图10给出了这种实用的辉光数码管译码电路。(张晋纯 宋东生编译)