随着科学技术的飞速发展,目前声频技术已进入了数字化音响时代。不少读者可能开始接触到数字式唱片系统、数字式录音机、电视唱片、数字式无线电广播等新设备和新技术,那么这种数字音响技术的原理是什么呢?
翻开音响技术发展的历史,我们可以发现,从1877年爱迪生发明圆筒式留声机算起,以后近百年的时间里,声音的记录、储存、传送和再生,一直都是采用模拟方式,所使用的都是模拟信号。模拟信号的特点可用图1来说明。图中纵座标轴代表信号的幅度,模座标代表时间,不难看出,信号幅度值随时间的变化是连续的,不是间断的。通常我们所听到的人的说话声、乐器声以及自然界里的各种声音、都是模拟信号。普通录音机、收音机、扩音机和电唱机等所处理的信号,也都是模拟信号。这类信号的优点是处理方式比较简单和方便,但它也有不可克服的缺点,例如在进行高传真录音和放音时,经过多次的录音和放音后,信号源(如磁带)中的噪音和失真会积累增加,信号的动态范围也会缩小。

随着人们欣偿能力的提高,对音乐质量越来越高的要求,采用模拟方式的高传真音响系统已远远不能满足要求,于是,世界各国的音响工程师们经过多年的努力,研究出一种崭新的数字音响技术。它的基本思路是先通过一种特殊的PCM技术——即脉冲编码调制技术,将我们通常所使用的模拟信号转换成一组一组的数字信号,然后用数字式音响设备对这种信号去进行记录、储存和传送。信号再生时,通过脉冲解码技术,将数字信号还原成模拟信号,经放大后再去推动杨声器放音。
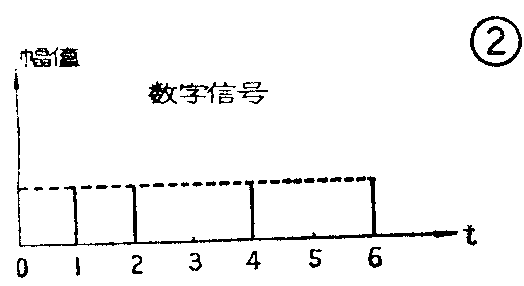
所谓“数字”,大家都知道,是1、2、3……(十进制)或0、1(二进制)等,引伸后也可广泛地指不连续或者“离散”的阶跃的意思。因此数字信号也就是指在时间和取值上都不连续变化的信号。图2就是一种数字信号的例子,可以看出,它与图1模拟信号的结构是完全不同的。它在时间轴上的取值是不连续的,只在t=0、1、2、3、4、5、6等离散时刻,在纵座标轴上才给出相应的值,在其它时间是没有意义的。另外还可以看出,纵座标轴上取值的大小只有“0”和“l”两种可能。原模拟信号在幅度和频率上的千变万化,在这里仅是借助于“0”和“1”有规律的编码组合来反映的,有脉冲的时候为“1”,无脉冲时为“0”,所以数字信号实际上就是一组一组的有规律的脉冲。正是由于数字音响设备所处理的只是“0”和“1”这两种极简单的数码,所以它对各种干扰信号具有极强的抵抗能力。数字式音响设备的频带很宽,信号畸变甚小,噪音很低,信号的动态范围可达90~100dB,远远优于模拟音响设备。例如有些数字式录音机和数字式唱机,其抖晃率和噪音等指标已小到仪器无法测出的地步,这是模拟音响系统所望尘莫及的。
许多读者可能会问,幅度和频率都千变万化的模拟信号,是怎样转换成类似图2那样的一组一组的数字信号呢?而数字信号又是怎样逼真地还原出原来的模拟信号呢?这就是下面我们要着重讲一讲的PCM技术。
PCM三个字母是英文Pulse Code Modulation的缩写,中文意思是“脉冲编码调制”,它是把模拟信号变换成数字信号的一种方法。
PCM原理可用图3来解释说明。图3(a)是一个一般模拟信号波形,首先以一定时间间隔的脉冲取出模拟信号相应时刻的幅度值,如图3(b)所示,这个过程叫做取样,每秒钟取样的次数,即每秒钟取出电压幅度值的个数叫做取样频率。不难看出,经过取样,信号在时间取值上已呈不连续状态,但在幅度取值上仍然是连续的,所以取样的过程,实际上就是把模拟信号的时间轴加以离散化,把模拟信号变换成脉冲调幅信号。为了在解码时能够逼真地还原出原始模拟信号,取样频率越高越好。但考虑到取样频率太高时设备太复杂,因此可以认为只要使取样频率大于模拟信号最高频率的两倍即可不失真地还原出原来的模拟信号,所以要保证音频信号20HZ~20KHz的带宽,只要取样频率大于40KHz即可。
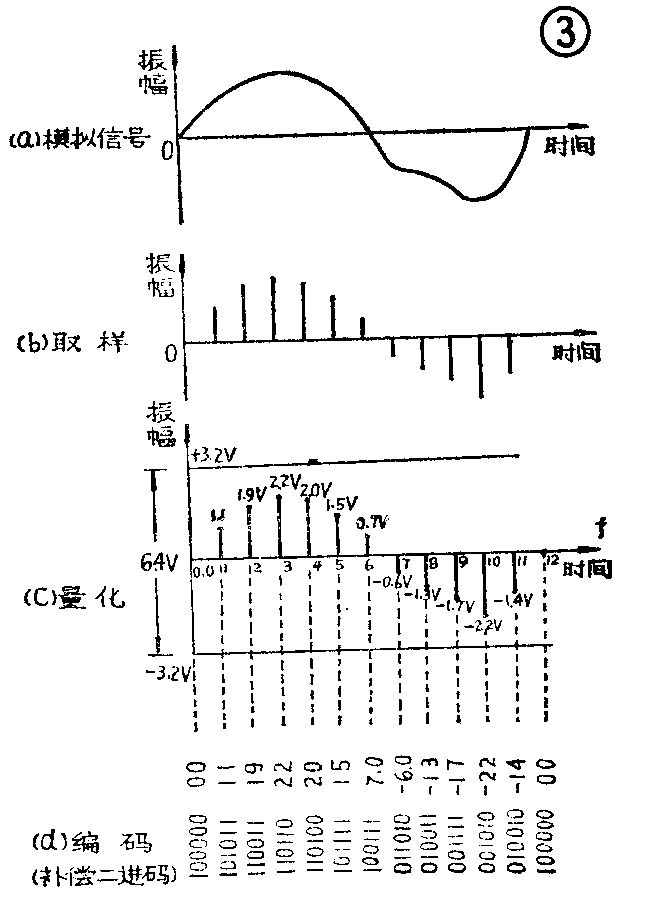
取样以后,再对信号的幅值进行量化和编码。所谓量化,就是将每个脉冲连续变化的幅度值离散化,使其成为一个一个不连续变化的、阶跃的幅值。这就象我们平时衡量某项产品的质量,将其质量由次到好这样一个连续变化的过程平均分成几个等级,例如分成五级,使其质量靠近一级的都算成一级,靠近二级的都算成二级……,这样就便于人们对产品的质量进行计量了;所谓编码,就是将量化后用十进制表示的不连续的幅度值用极简单的二进制编码来表示,以便于用数字电路来处理这些编码信号。这就象大家熟悉的发电报一样,它是将每个汉字按一定规律化成一组一组的编码,传送起来就很方便了。下面我们具体举一个例子:设图3C中原模拟信号的幅度变化的动态范围为6.4V(即正方向变化3.2V,负方向变化3.2V,见图),现在我们想用由六位二进制数码(即六个0和1组成的数码,也可以叫做六比特)组成的编码,来表示在信号动态范围内的一些不连续的幅值,我们知道,当选用六位二进制时,其编码可有2\(^{6}\)=64组,也就是说,可以用这64组二进制编码来表示信号动态范围6.4V内的64个不连续变化的幅度值。那么是怎样具体换算和表示的呢?方法是将6.4V被64除,将6.4V分成64个小等分,每一小等分的幅值为6.464=0.1V,我们令这一小单位幅度为基准幅度,用它分别去除取样后每个脉冲的实际幅值,将所得商数用四舍五入的法则使其整数化,这一过程就叫做“量化”。以图3C来说,在t=1时,原脉冲幅度为1.1V,除以0.1V后,得到量化值11;在t=2时,得到量化值为19;在t=10时,得到量化值为-22;等等。上面几个脉冲幅值都能被0.1整除,即小数点后面没有数了,所以不需再进行四舍五入。如果量化值存在小数部分,如11.4、18.6等,则应依四舍五入法则,处理为11和19。通过上面分析可以看出,选用的二进制数码的位数越多,即比特值越大,脉冲编码的组数就越多,于是就可以将脉冲的幅度分得更细一些,量化的基准幅度可以取得更小,量化误差也就更小,信号的动态范围也就可以加大。
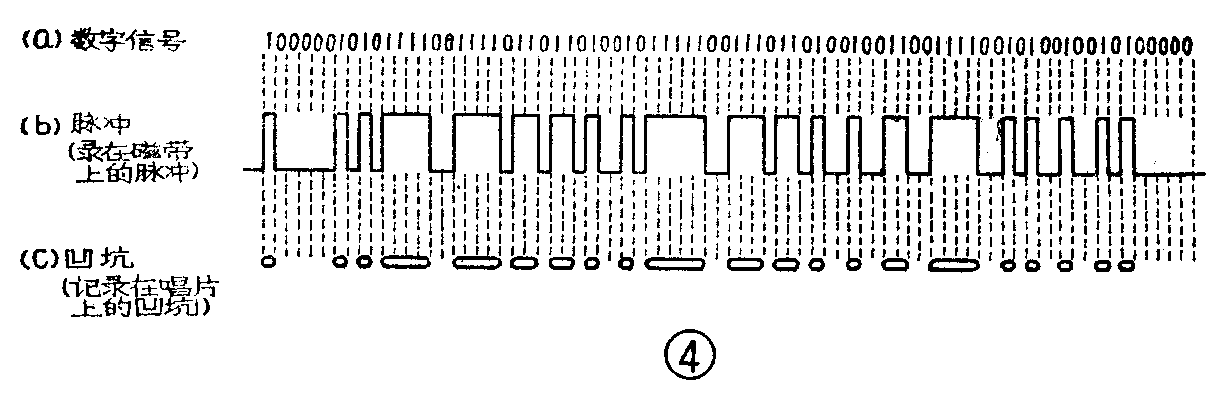
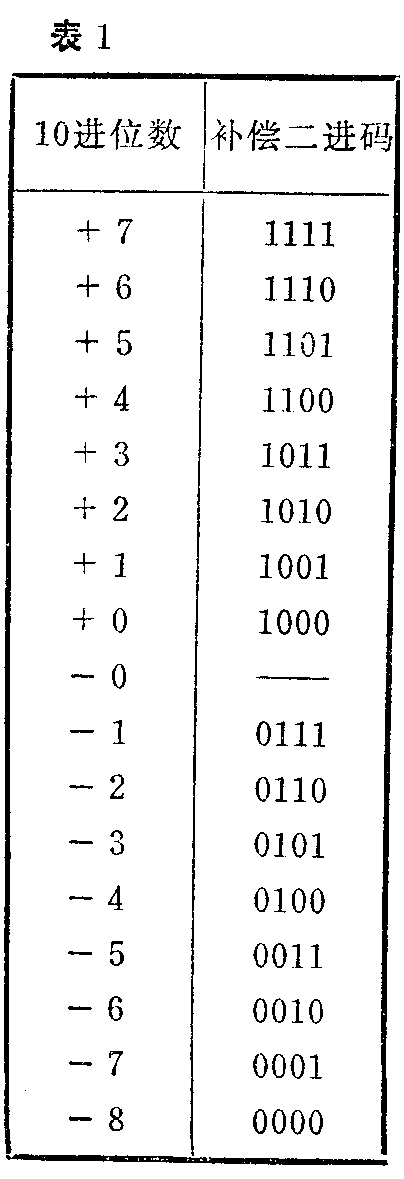
从图3C中还可以看出,量化后的每个脉冲的幅度值是以十进位数码表示的,使用时还必须把十进位数变为二进位数码,这个过程叫做“编码”。二进位制的编码有许多种形式,本文采用的是一种较简单的补偿二进码,它的编码规律见表1(这组编码的比特值为4,可获得2\(^{4}\)=16组编码)。按照这种编码规律,将其用于本文六位二进制的情况,则十进数“0”表示为100000,“1”表示为100001,“2”表示为100010,“3”表示为100011,等等。也就是说,凡十进位制大于0的数,化成二进位制时,都是在100000这个基础上相加的;十进位负值的表示方法是,在100000的基础上相减。例如:十进制的“-1”表示为100000-000001=011111,“-2”表示为100000-000010=011110,“-3”表示为011101,等。这种编码适合用于幅度有正、负变化的信号。将这种编码用于图3C,就可以将各个量化值表示成图3d形式的一组一组的编码。这样模拟信号经过取样、量化和编码三个过程(实际上量化和编码是同时进行的),就被转换成一组一组的数字信号,完成了模拟/数字的转换任务。最后再把图4a经过编码的数字信号调变成如图4b那样的等幅数字脉冲信号(无脉冲时为“0”,有脉冲时为“1”),并且记录在磁带上。或者也可以用它去控制激光器的光束,激光束照射在一涂有感光材料的玻璃圆盘上,使圆盘一会儿曝光,一会儿不曝光,于是在圆盘上留下了如图4C那样的一系列凹坑(这就是激光唱片的原理),这就完成了数字音响的记录过程。重放上述数字信号时,只要经过数字/模拟变换器把数字信号转换成模拟信号,并通过低通滤波器把超过20千赫的高频成分滤除掉,恢复出原来的模拟音频信号,再经过音频功率放大器放大,便可通过扬声器把音响播放出来。(梁宣虎 卢旭生)