在电子计算机和各种数字化电子设备中,计数器是最基本的部件之一,它能累计和寄存输入脉冲的数目,就象人们计数一样:“1、2、3、4……”,最后给出累计的总数。
数字电路中的计数制——二进制
数字电路中普遍采用着二进计数制(简称二进制)。在二进制数列中,每一位只可能有0和1两个数码,而相邻两位的关系是“逢2进1”。例如:
1 10 11 100 101 110 111
+ 1 + 1 + 1 + 1 + 1 + 1 + 1
── ── ── ── ── ── ──
10 11 10O 101 110 111 1000
这就是说,每当本位是1,再加上1时,本位就变成0,向高位进位,使高位加1;当本位是0,再加上1时,本位变成1。二进制与十进制的对应关系如附表所示。
二进制
十进制
第四位2\(^{3}\) 第三位22 第二位2\(^{1}\) 第一位20
0 0 0 0 0
1 0 0 0 1
2 0 0 1 0
3 0 0 1 1
4 0 1 0 0
5 0 1 0 1
6 0 1 1 0
7 0 1 1 1
8 1 0 0 0
9 1 0 0 1
10 1 0 1 0
11 1 0 1 1
12 1 1 0 0
13 1 1 0 1
14 1 1 1 0
15 1 1 1 1
为什么数字电路中不用十进制却要使用二进制呢?这是因为十进制有十个数码0、1、2、3、4、5、6、7、8、9”,要求一种电路或元件具备十种不同的状态来代表这十个不同的数码是相当困难的,而用两种截然不同的状态表示1和0却很容易实现。例如:用高电位表示“1”,低电位表示“0”;有脉冲表示“1”,无脉冲表示“0”;开关断开表示“1”,开关接通表示“0”,等等。但是,在生产和生活中,人们习惯于使用十进制,所以用二进制计数的结果还需要“翻译”成相对应的十进制数字,这个职能可以由一种称为“译码器”的电路来实现。译码器输出的十进制数字最后通过“显示器件”直观地显示出来。
二进制计数器是怎样工作的
上一讲曾介绍过一种简单的T触发器,这种触发器的功能是每输入一个计数脉冲CP(又称时钟脉冲)就会翻转一次。图1绘出了带“复位(R)”端的T触发器工作情况示意图。在计数之前,先从R瑞输入一个负脉冲,使触发器的输出端变为低电平“0”,这个过程叫“复位”或“置0”。当在T端输入一个计数脉冲CP时,触发器翻转,Q端由低电平“0”变为高电平“1”,接着再输入第二个计数脉冲CP时,触发器再次翻转,Q端又由“1”回到“0”,这时Q端将输出一个脉冲,称为进位脉冲。显而易见,T触发器每输入两个计数脉冲,就能输出一个进位脉冲,具有“逢2进1”的计数功能。所以,一个T触发器实际上就是一个一位二进制计数器。
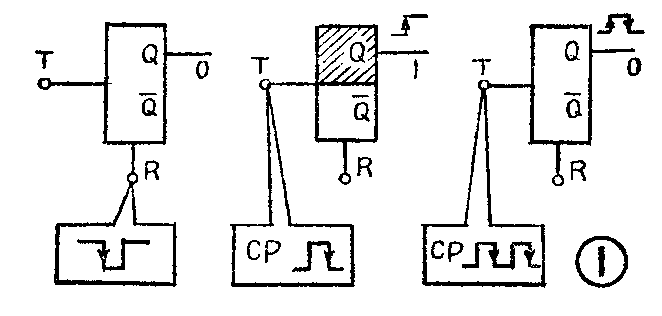
图2是把四个T触发器串联起来构成的四位二进制计数器示意图。当在R端加上负脉冲时,各位触发器的输出端子不管原来处于什么状态,都将变为低电平“0”。也就是在重新计数之前先把各位触发器都“置0”
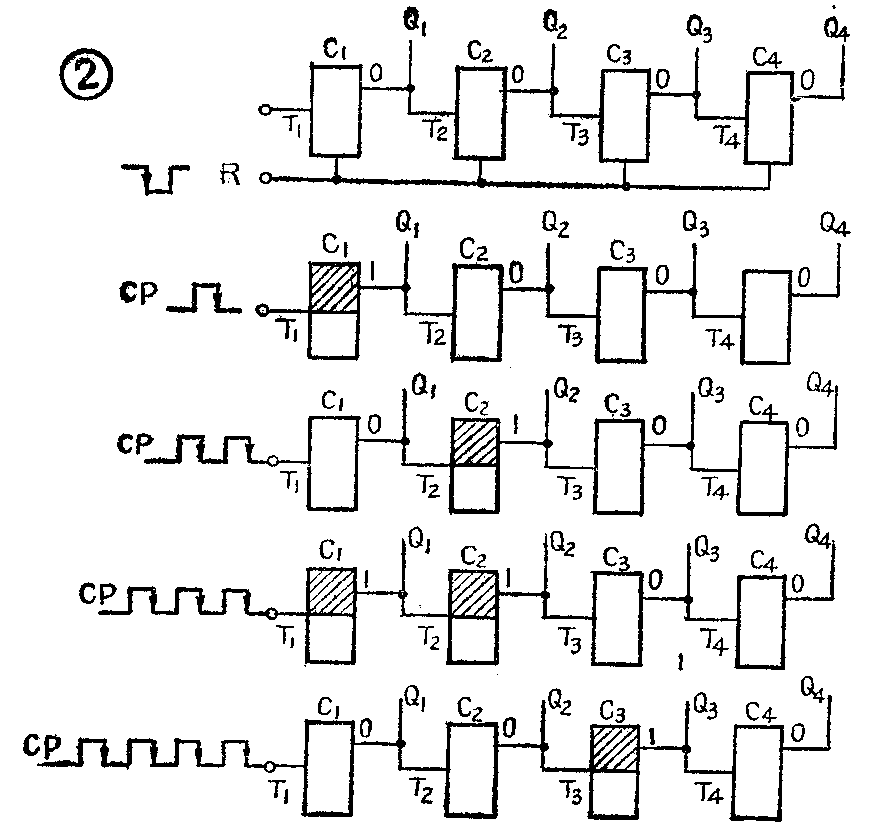
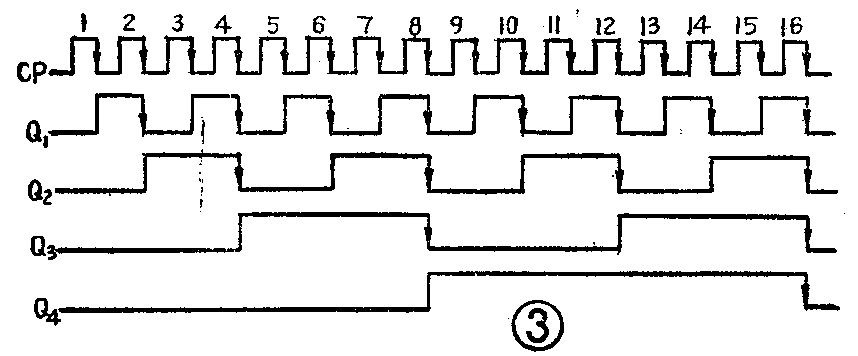
当第一个计数脉冲到来时,触发器C\(_{1}\)(2\(^{0}\)位)翻转,Q1由“0”变“1”。由于所用的触发器是用计数脉冲的负跳变沿触发的,所以Q\(_{1}\)端电平由“0”变“1”时产生的正跳变对高一位(21位)触发器C2没有影响,C\(_{2}\)不会发生翻转,C3、C\(_{4}\)更不会翻转,这时计数器的状态是“0001”。第二个计数脉冲到来时,C1又翻转一次,Q\(_{1}\)由“1”变“0”,出现负跳变,使触发器C2翻转,Q\(_{2}\)由“0”变“1”(正跳变),C3、C\(_{4}\)都不会翻转,于是计数器的状态变为“0010”。第三个计数脉冲到来时, C1翻转,Q\(_{1}\)由“0”变“1”,因此C2不会翻转,C\(_{3}\)、C4也不会翻转,计数器的状态是“0011”。第四个计数脉冲到来时,C\(_{1}\)再次翻转,Q1由“1”变“0”,使C\(_{2}\)翻转,Q2由“1”变“0”(负跳变),又使C\(_{3}\)(2\(^{2}\)位)翻转,Q3由“0”变“1”,所以C\(_{4}\)不会翻转,计数器的状态变为“0100”……。如此继续下去.一直到第十五个计数脉冲到来时,计数器的状态变为“1111”。在计数过程中各位触发器的输出状态与输入计数脉冲数之间的关系可用图3所示的波形图直观地表示。显然,它与附表给出的结果完全一致。如果再来第十六个计数脉冲,则各位触发器的Q输出端全变为“0”,计数器的状态回到“0000”,这时,C4将输出一个进位脉冲。由图3可见,四位二进制计数器的第一位触发器C\(_{1}\)是每来一个计数脉冲就翻转一次;第二位触发器C2是在C\(_{1}\)由“1”变“0”(即有进位)时才翻转一次;第三位触发器C3是在第二位由“1”变“0”有进位时才翻转一次;第四位触发器C\(_{4}\)是在第三位有进位时才翻转,从而实现了二进制计数。四个触发器串联后,认输出与输入的关系来看,每输入十六个计数脉冲,输出一个进位脉冲,所以它又是一个十六进制计数器。
如何实现十进制计数
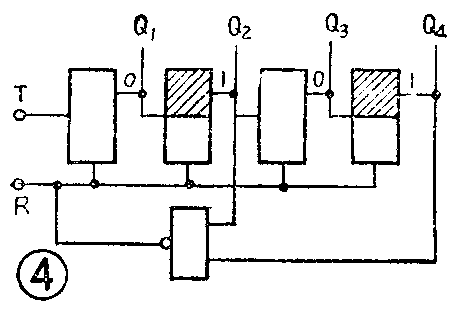
在数字设备中常常采用十进制计数器。怎样组成一个十进制计数器呢?一个T触发器具有“逢2进1”的功能;用两个T触发器串连能做到“逢4进1”;用三个能做到“逢8进1”;用四个能做到“逢16进1”。但十进制计数器却要求做到“逢10进1”,因此,要用四个触发器并在线路上采取措施,使第十个计数脉冲到来时,触发器输出端状态变为“0000”,实现“逢10进1”。上述四位二进制计数器在输入第十个计数脉冲时,四位触发器的输出状态应为“1010”,即C\(_{4}\)和C2两触发器的输出端都是高电平“1”,如果按图4的方法,把C\(_{4}\)和C2两个触发器输出的高电平“1”,同时输入一个“与非门”,则与非门将输出一负脉冲,再将这个负脉冲同时加到各触发器的“复位”端(R端),就能在第十个计数脉冲到来时,使计数器的状态成为“0000”,再重新开始计数并进位,实现“逢10进1”。
任意进制的计数器
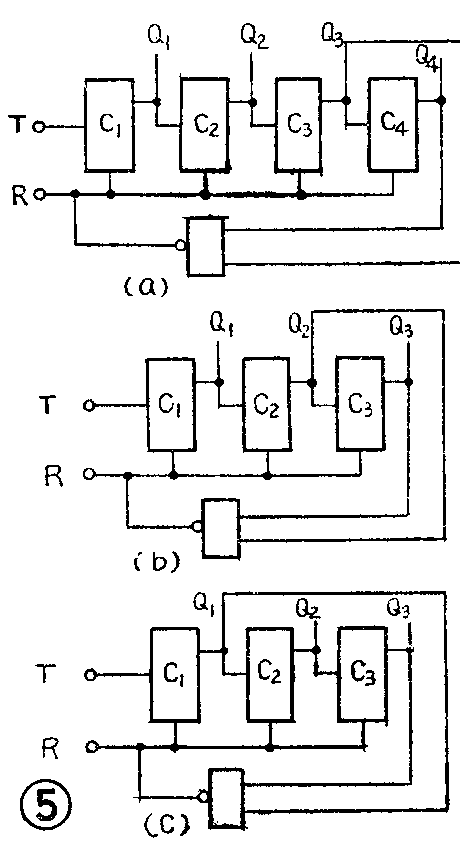
根据上述十进制计数器的电路原理,参照表1,把几个T触发器和与非门进行适当组合,就能构成最简单的任意进制的计数器。图5分别给出了十二进制、六进制和五进制计数器的逻辑图。其它进制计数器的原理也是一样的。(张晋纯 宋东生 编译)