初学无线电同志在使用阻容元件时可能会提出这样的问题:为什么有时找不到自己所需数值的阻容元件?为什么阻容元件的标称值大多不是整数?例如是110Ω、6.8K、220PF、0.047μF等一些令人难以琢磨的“怪数值”。当阻容元件的标称值与所需值不同时,如何选择阻容元件呢,下面我们就来谈谈这个问题。
为了满足使用者的各种不同需要,阻容元件厂要生产各种不同阻值、容量的电阻器和电容器。但是不可能也没有必要使用者要什么数值,工厂就生产什么数值的阻容元件。大量生产的阻容元件其成品值不可能做得一模一样,总会有一点误差。
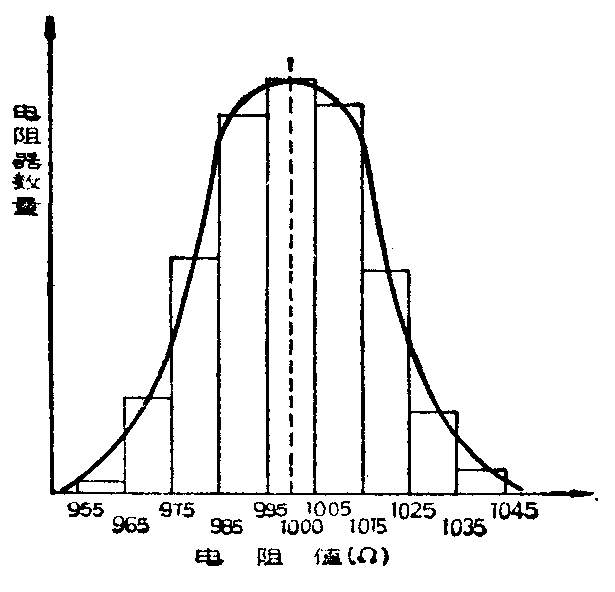
例如生产一批阻值为1000Ω的电阻器,制成以后的电阻器不可能全部都是1000Ω,而是在1000Ω左右。如果我们把这些电阻器按每相差10Ω分成若干组,就会发现接近1000Ω的最多,与1000Ω相差越大的越少。这个规律可以绘成如附图所示的曲线。这个曲线叫做正态分布曲线。在正常状态下生产的阻容元件,其实际值都符合这样的分布规律。为了便于大量生产,同时也让使用者在一定的允许误差范围内选用阻容元件,我们总希望在使用者的允许误差范围内,将阻容元件的规格数减小到最少。利用几何级数可以达到上述要求。几何级数的通项公式为:
a\(_{n}\)=arn-1
这里a\(_{n}\)表示该几何级数的第n项;
a为几何级数的首项;
r表示几何级数的公比;
n表示项数。
如果公比r被选择为10的k次方根,并且设首项为1的话,那么:
a\(_{n}\)=1×(\(\sqrt{k}\)\(^{1}\)0)n-1
我们知道,一个几何级数,其公比越小每项的相差就越小。利用这一情况,可以根据分组粗细的要求来决定k值。若要求分组细,k就要用得大一些,否则k可小一点,例如若在10以内要求有三个值,k选为3,那么公比是2.154,三个四舍五入值分别为1、2.15、4.64。若k选为6,则公比是1.468左右,在10以内分为:1、1.468、2.154。3.163、4.64、6.812,四舍五入后再取接近值:1、1.5、2.2、3.3、4.7、6.8。
阻容元件的标称值系列是将k分别选择为6、12、24、48、96、192所得值化整后构成的。即E6系列、E12系列、E24系列、E48系列、E96系列和E192系列,分别适用于允许偏差为±20%、±10%、±5%、±2%、±1%、±0.5%的阻容元件。E6、E12、E14的各系列值,见附表。
从表中不难分析,这种标称值系列的优越性就在于:在同一系列相邻两值中较小数值的正偏差与较大数值的负偏差彼此衔接或叠接(也有少数值由于计算化整的原因而略有间隙)。例如在E6系列中。数值1.0的正偏差极限是(1.0+1.0×20%)=1.2与下一个数值1.5的负偏差极限(1.5-1.5×20%)=1.2正好衔接;在E24系列中,数值4.7的正偏差极限(4.7+4.7×5%)=4.935与下一个数值5.1的负偏差极限(5.1-5.1×5%)=4.845叠接。
正因为这种标称值系列的偏差极限是衔接或叠接的,所以无论元件的实际值与规格值的偏差大小,都可以按照一定系列(E6,E12,E24……)把它们归于某一标称值。也就是说除非元件其它参数有缺陷而成为废品外,所有制造出来的元件,不管它的实际值是多少都可以按照一定标称值和误差分选,即做到“无废品生产”。
反过来,如果我们采用1.0、1.5、2.0、2.5……10这样的惯用数来制造元件,按其一规格值和一定偏差分选时,可能有些元件无法归入任意一个规格而成为不是废品的“废品”。例如规定误差为±5%,实际值大于(100+100×5%)=105小于(150-150×5%)=142.5之间的产品就既不能标100也不能标150,而成为不是废品的“废品”。
十进标称 E24 E12 E6
值系列
误差 ±5% ±10% ±20%
电 1.0 1.0 1.0
阻 1.1
器 1.2 1.2
电 1.3
容 1.5 1.5 1.5
器 1.6
标 1.8 1.8
称 2.0
值 2.2 2.2 2.2
2.4
2.7 2.7
3.0
3.3 3.3 3.3
3.6
3.9 3.9
4.3
4.7 4.7 4.7
5.1
5.6 5.6
6.2
6.8 6.8 6.8
7.5
8.2 8.2
9.1
由于表列这种经标准化了的阻容元件标称值系列既能满足使用者对规格的各种要求,又能使生产的规格简化到最少的数量,所以除特殊需要外,工业上大量生产的电阻器(包括电位器)、电容器的标称值都符合附表中各数值再乘以10\(^{n}\),其中n为正整数或负整数。(王兴禄)