在研究OTL功率放大器时经常遇到这样两种情况,一种是给定一个数据齐全的OTL电路,要求核算(或估算)一下它的最大不失真输出功率;另一种是给定额定最大不失真输出功率,要求设计一个OTL电路。不管是核算还是设计,都要弄清楚OTL电路的最大不失真输出功率究竟与什么有关。为此,我们以图1所示的互补对称OTL电路为例,来研究其最大不失真输出功率。
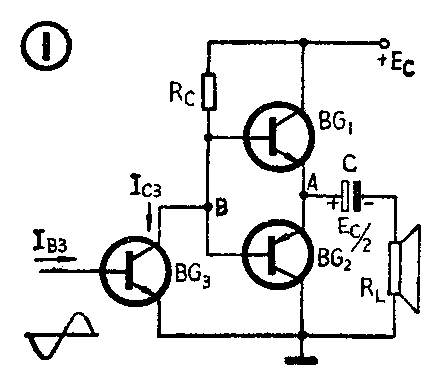
假设输出管BG\(_{1}\)和BG2的特性对称,那么静态时A点的电位V\(_{A}\)=EC2。由于静态时负载(喇叭)上没有电流,因此电容C两端的电压V\(_{C}\)也是EC;2。当激励级BG\(_{3}\)的输入信号为负半周时,IB3减小,I\(_{C3}\)减小, 电阻RC上的电压V\(_{RC}\)=IC3R\(_{C}\)也减小,所以使B点电位升高,结果输出管BG1导通,BG\(_{2}\)截止。当激励级BG3的输入信号为正半周时,I\(_{B3}\)增加,IC3增加,电阻R\(_{C}\)上的电压VRC=I\(_{C3}\)RC增大,所以B点电位降低,结果使输出管BG\(_{1}\)截止,BG2导通,完成两管推挽工作。
为了获得最大不失真输出功率,一般要求激励级输入信号在正负峰值时,激励管BG\(_{3}\)应恰好达到饱和与截止状态。
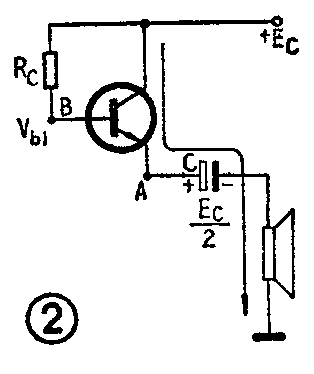
下面我们先来研究激励级输入信号负半周峰值时的情况。这时BG\(_{3}\)截止,B点电位升高,BG2也截止,BG\(_{1}\)趋向饱和。于是OTL电路输出级便可等效为图2。A点电位达到最大值VAm,但不是E\(_{C}\),而是受BG1饱和压降V\(_{ces1}\)的限制,所以VAm=E\(_{C}\)-Vces1。
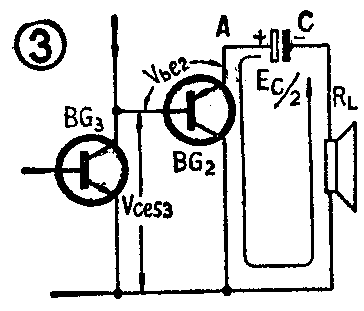
现在再来研究激励级输入信号正半周峰值时的情况。这时BG\(_{3}\)饱和,B点电位降低,BG1截止,BG\(_{2}\) 趋向饱和。于是OTL电路输出级便可等效为图3。A点电位达到最小值VAn,但不为零,而是与零电位差一个饱和压降V\(_{ces2}\),即VAn=V\(_{ces2}\)。
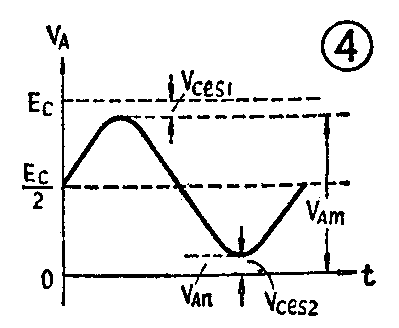
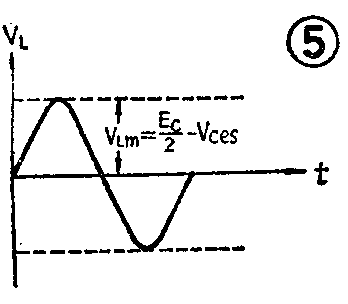
综合上面情况可以画出在激励级输入信号一周期变化时A点电位的波形如图4。若BG\(_{1}\)与BG2的特性一致,则V\(_{ces1}\)=Vces2=V\(_{ces}\)。由图4可以看出,A点电位以EC2为中心上下摆动,其摆动的振幅为(EC;2-V\(_{ces}\))=\(\frac{1}{2}\)(Ec-2V\(_{ces}\))。由于电容C的隔直作用,负载RL上所得的波形如图5。我们令输出管的集电极最大不失真输出功率为P\(_{om}\),负载上得到最大不失真功率为PLm,由于电容C上无交流电压,因此这时P\(_{om}\)=PLm。如何求P\(_{om}\)呢?我们知道正弦波的功率等于电压有效值VL与电流有效值I\(_{L}\)的乘积。这里负载上的电流IL就是输出管的发射极电流,也近似等于输出管的集电极电流。根据有效值电流或电压是振幅值的1;\(\sqrt{2}\)倍的关系可得:
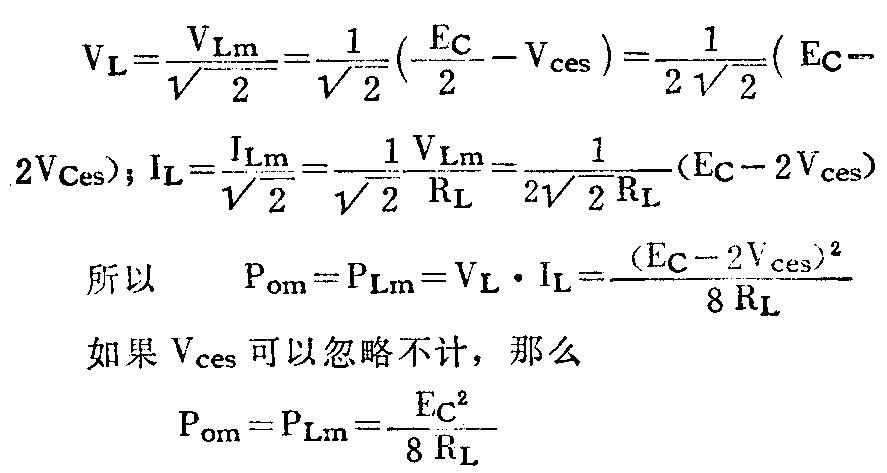
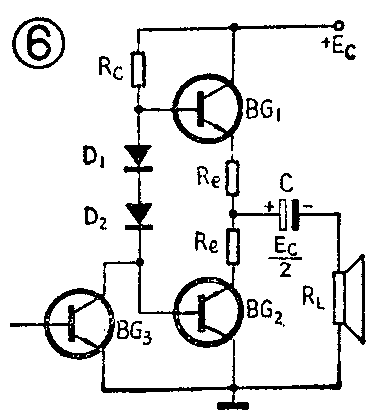
一般OTL电路输出管发射极都接一小电阻R\(_{e}\)以稳定工作点,如图6所示。图中D1D\(_{2}\)是为了克服交越失真给输出管一定偏流而设置的。如果考虑Re,这时晶体管集电极最大不失真输出功率P\(_{om}\)就不等于负载RL上的最大不失真功率P\(_{Lm}\),因为Re上还要消耗功率。这时P\(_{om}\)等于Re与R\(_{L}\)上的功率的总和,即
P\(_{om}\)=Ve·I\(_{L}\),Ve是发射极对地交流电压的有效值。
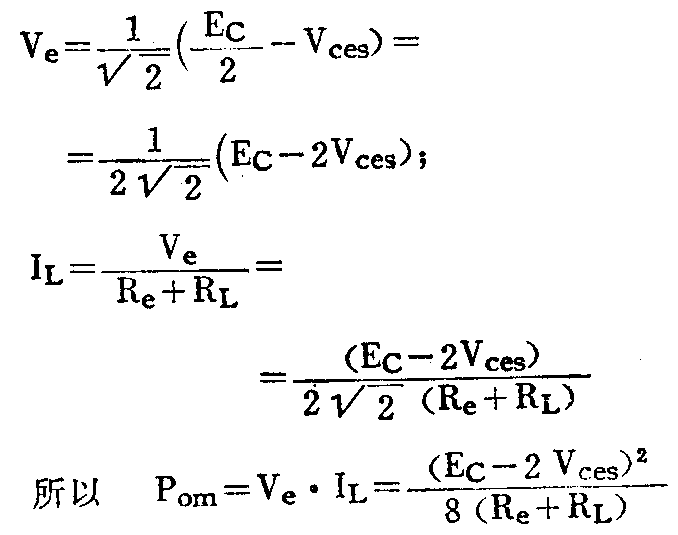
而负载R\(_{L}\)上得到的最大不失真功率可按分压关系得到
P\(_{Lm}\)=(EC-2V\(_{ces}\))\(^{2}\)8(Re+R\(_{L}\))·RL;R\(_{e}\)+RL
在实际工程核算或设计中主要是运用近似公式P\(_{om}\)≈EC\(^{2}\)8R\(_{L}\)。现在我们来谈谈这个近似公式的实际运用。
(1)由P\(_{om}\)=EC\(^{2}\)8R\(_{L}\)近似公式来估算OTL电路的最大不失真功率。
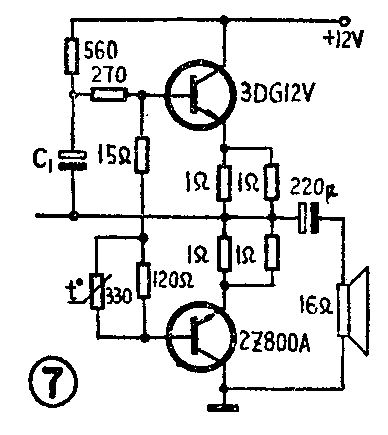
我们通过一个具体电路来说明这个问题。图7为联合设计23cm电视机低放电路的输出级。在忽略V\(_{ces}\)和不计Re的情况下,负载上得到的最大不失真功率P\(_{Lm}\)=EC\(^{2}\)8R\(_{L}\)=122;8×16≈1.1瓦。如果不忽略Vces并设V\(_{ces}\)=1V,而又不计Re的情况下,负载上得到的PLm=(E\(_{C}\)-2Vces)\(^{2}\)8×R\(_{L}\)=(12-2)2;8×16≈0.78瓦。在不忽略Vces和Re的情况下,负载上得到的P\(_{Lm}\)=(EC-2V\(_{ces}\))\(^{2}\)8(RL+R\(_{e}\))×RL;R\(_{b}\)+Re≈0.7瓦。我们知道了上面几种情况下的功率数量关系后,作为估计只需通过P\(_{om}\)=EC28R\(_{L}\)公式计算得出1瓦左右,然后打个折扣如按60~70%估算即可。又如已知喇叭阻抗RL= 8Ω,电源电压E\(_{C}\)=24V的扩音机,大致估算在喇叭上能得到多大功率。通过Pom≈E\(_{C}\)\(^{2}\);8RL=2428×8=9瓦,然后将喇叭上得到的功率按60%折算,即为P\(_{Lm}\)=0.6×Pom=9×0.6≈5瓦左右。
(2)由P\(_{om}\)=EC\(^{2}\)8R\(_{L}\)近似公式可以明显看出提高OTL电路输出功率的途径。
由公式可见,在负载R\(_{L}\)给定的情况下,要想提高最大不失真输出功率只有增加电源电压EC。不过需要注意,由于这时输出最大电流I\(_{Lm}\)=EC2\(_{RL}\)也随之增加,因此必须检验一下输出管最大允许集电极电流ICm是否大于I\(_{Lm}\),ILm是不能超过I\(_{Cm}\)的,同时电源电压的增加,也要受到晶体管击穿电压的限制。
由近似公式可知,当电源电压给定的情况下,要想提高最大不失真输出功率,只有减小负载电阻R\(_{L}\)。但这时输出最大电流ILm=\(\frac{E}{_{C}}\)2RL也要随之增加,同样需要满足I\(_{Cm}\)>ILm。需要注意,减小负载电阻R\(_{L}\),在ICm>I\(_{Lm}\)的情况下可以提高最大不失真输出功率,但这是有条件的。就是必须保证激励级提供足够的激励。因为负载电阻减小后,要想得到更大的输出功率,显然要依靠输出管输出更大的集电极电流才成。如果激励级不能增加激励,那么输出管集电极电流也就不能增加。比如还和原来一样大小,于是得到的最大不失真功率就因为负载电阻减小反而会比原来小。有人将一部收音机的音量电位器开到最大还嫌音量不够,于是他按Pom=E\(_{C}\)\(^{2}\);8RL公式,换了一个阻抗小的喇叭,试图提高音量,结果适得其反。因为音量电位器已开得最大就意味着激励信号不能再增加了,而喇叭阻抗却减小了,所以音量反而更低了。
(3)P\(_{om}\)≈EC\(^{2}\)8R\(_{L}\)近似公式是设计OTL电路的最初依据。
一般设计都是给出负载电阻R\(_{L}\)和在负载上要求得到的最大不失真功率,然后通过设计来确定电源电压和选择输出级晶体管等。
例如已知R\(_{L}\)=8Ω,设计一个最大输出功率为3瓦的OTL电路的输出级。
根据P\(_{om}\)=EC\(^{2}\)8R\(_{L}\)得EC=\(\sqrt{8R}\)\(_{L}\)Pom=8×8×3=13.8V,考虑到饱和压降以及Re等因素,电源电压应留有足够的余量,一般留20%左右的余量,所以这时E\(_{C}\)'=EC×(1+20%)≈16.5V,再考虑到电源电压系列值,最后取E\(_{C}\)=18V。然后就可以根据EC=18V,R\(_{L}\)=8Ω条件去选择输出管。
因为一管截止时另一管接近饱和(相当于短路),这时电源电压几乎全部加在截止管上,因此,选管时必须考虑管子的BV\(_{ceo}\)≥EC=18V。另外,根据上面提到的管子的最大允许集电极电流I\(_{CM}\)要大于ILM,所以I\(_{CM}\)≥ILM=\(\frac{E}{_{C}}\)2RL=18;2×8≈1.13A。最后根据推挽电路能量关系的分析,管子最大允许集电极功耗P\(_{CM}\)必须大于0.2Pom,
P\(_{CM}\)≥0.2Pom=0.2×\(\frac{E}{_{C}}\)\(^{2}\)8RL=0.2×182;8×8≈1瓦
选用晶体管3AD6B可满足上述要求,其参数BV\(_{ceo}\)=24V;ICM=2A;P\(_{CM}\)=10瓦(加120×120×4mm\(^{3}\)散热片)。请注意,由于PCM>1瓦即可,所以无需加这么大的散热片。R\(_{e}\)一般选RL/10,故为0.5~1Ω。(赵学泉)