不对称比例鉴频器简易调试法

不对称比例鉴频器由于电路本身的结构特点，产生了一个十分简便的调试方法。该电路在元件选择、参数确定合理及装配无误的前提下，只需一块三用表（或表头），利用发射台的调频信号，就可以进行较好的调试，使电路工作在较佳状态。这一特点，对不具备扫频仪等专用仪表的业余无线电爱好者，无疑有其实用价值。本文欲就某电视接收机中伴音通道采用的较为典型的不对称比例鉴频器电路为例（原理电路图如图1所示），介绍它的调试原理和方法。

为弄清图1所示电路的简单调试原理，必须对该电路的结构特点和鉴频工作过程有一个简要的了解。

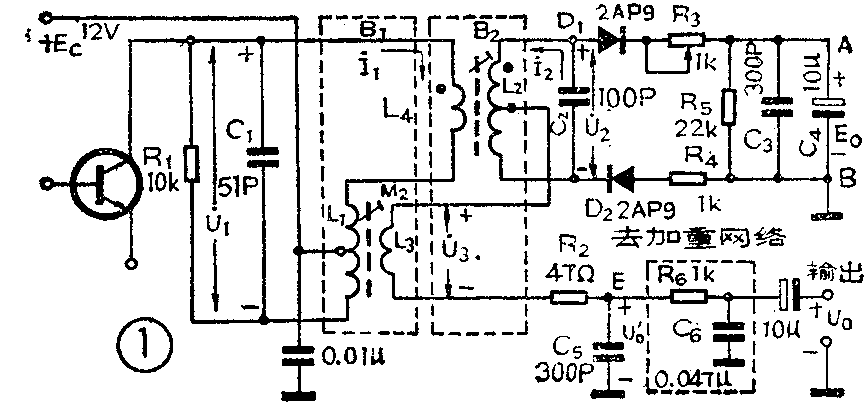
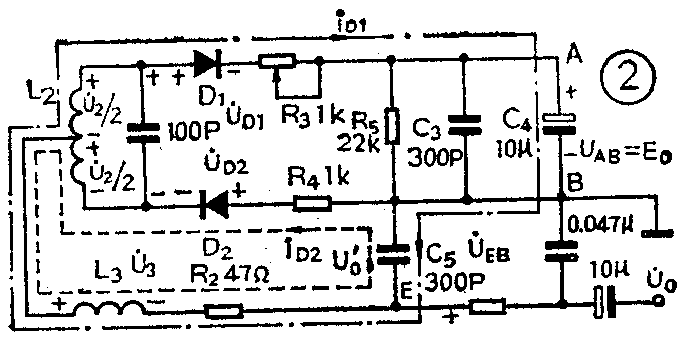
图1电路中，用LC并联耦合回路组成输入电路，L\(_{1}\)、L4和C\(_{1}\)是初级回路，L2、C\(_{2}\)是次级回路，初级回路和次级回路均谐振在调频波信号的中心频率fo上（本电路f\(_{o}\)=6.5MHz）。L4与L\(_{2}\)同绕在一个中周B2的磁心上，实现初、次级回路之间的紧耦合；L\(_{3}\)与L1同绕在另一个中周B\(_{1}\)的磁心上，L3以互感耦合的方式取得调频信号电压U·\(_{3}\)（U·3=μU·\(_{1}\)即U·3与U·\(_{1}\)同相，μ是与互感M及电感L有关的比例系数）作为基准信号电压，以便和次级回路L2二端的电压U·\(_{2}\)（U·2为次级回路二端的调频信号电压）进行矢量迭加，形成由D\(_{1}\)、D2及有关元件组成的两个峰值检波器的高频输入信号电压U·\(_{D1}\)和U·D2，见图2（其中电压“U·”的点“·”表示该量为矢量）。

为了实现鉴频，电路完成了二个转换过程：一是将信号频率的变化转换成相位的变化；二是将相位的变化转换成幅度的变化，再将此幅度的变化用二个检波器差动检出，这就完成了鉴频的全过程。

下面分析一下频相转换过程：如上所述，U·\(_{3}\)和U·2在二个检波器输入端进行矢量迭加，若U·\(_{3}\)和U·2的相位关系反映了U·\(_{1}\)的频率变化规律，就达到了频相转换的目的。如图1所示，由电感的端电压和流过电感的电流的相位关系可知：I·1滞后U·\(_{1}\)90°（I·1为流过初级回路电感的电流），I·\(_{1}\)通过初、次级回路之间的互感耦合作用，在次级回路中产生感应电动势E·2=jωMI·\(_{1}\)（在图1所示正方向下），可见E·2超前I·\(_{1}\)90°，则E·2与U·\(_{1}\)同相；E·2在次级回路产生感应电流I·\(_{2}\)近似为（忽略初、次级间的反射阻抗）

（r为次级回路等效损耗电阻；E\(_{2}\)相当于串接在次级回路中）

在回路谐振时（即f=f\(_{o}\)，ω=ωo=1\(\sqrt{L}\)\(_{2}\)·C2），回路电抗部分为零（ωL\(_{2}\)=1/ωC2），则有

I·\(_{2}\)=E·2r，此时I·\(_{2}\)与E·2同相，即I·\(_{2}\)与U·l同相；U·\(_{2}\)为次级回路的端电压（即L2上的端电压），所以U·\(_{2}\)超前I·290°，即在谐振时，有U·\(_{2}\)超前U·190°的相位关系，或者说此时U·\(_{2}\)与U·1二矢量相互垂直，如图3所示。因U·\(_{3}\)与U·1同相，所以U·\(_{2}\)与U·3在f=f\(_{o}\)时相互垂直。

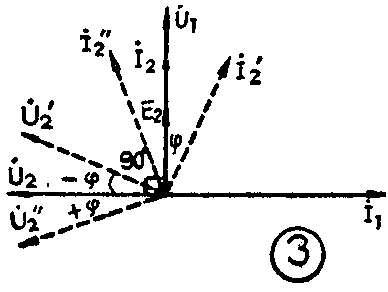
若已将回路调谐于中心频率f\(_{o}\)，但加于回路的调频信号频率f随调制信号在中心频率fo上下变化，即f＞f\(_{o}\)或f＜fo产生失谐，则LC并联回路就要产生附加相移ф，其相频特性曲线如图4所示。在失谐状态下，U·\(_{2}\)与U·1间的相位关系为90°＋ф。由图4可知：当f＞f\(_{o}\)时，ф＜0，为负的相移，则U·2超前于U·\(_{1}\)的相角小于90°（90°-ф）；当f＜fo时，ф＞0为一正的相移，则U·\(_{2}\)超前于U·l的相角大于90°（90°＋ф）；f=f\(_{o}\)时，ф=0，U·2超前U·\(_{1}\)90°；上述情况表明相移反映了频率的变化。这样由于耦合回路的作用，实现了频相转换。

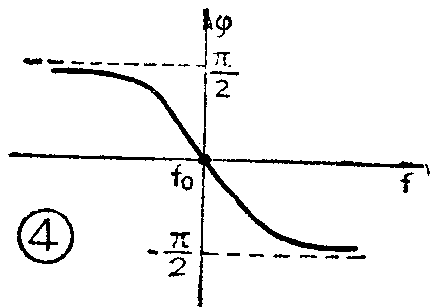
关于相、幅的转换过程，我们用矢量合成法来说明。如图2所示；\(\frac{1}{2}\)U·\(_{2}\)、U·3均为高频调频波信号，对于高频而言，C\(_{3}\)、C4、C\(_{5}\)均可视为短路，若忽略辅助元件R2、R\(_{3}\)、R4的作用，则图2的高频等效电路如图5所示、U·\(_{D1}\)、U·D2为加到两检波二极管D\(_{1}\)、D2上的高频信号电压，由图5显见存在如下关系式：

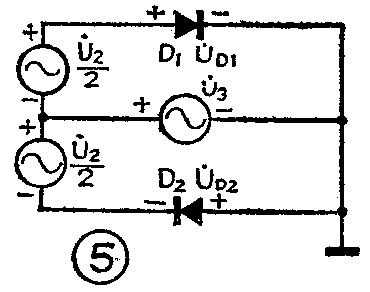
U·\(_{2}\)与U·3间的相位关系我们已经知道，则\(\frac{1}{2}\)U·\(_{2}\)、U·3、-U·\(_{3}\)间的相位关系我们当然也知道。这样，（1）、（2）二式所表达的各参量之间的关系可分三种情况即f=fo，f＞f\(_{o}\)，f＜fo，用矢量合成的方法（可形象的述为平行四边形法）表达如图6所示。（这里用到了在矢量图上进行矢量和差运算的概念。）

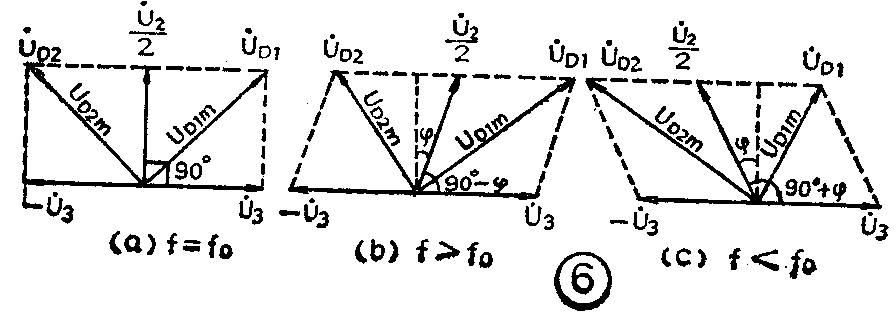
由图6可知：当f=f\(_{o}\)时，ф=0，\(\frac{1}{2}\)U·2超前U·\(_{3}\)90°，则加到二极管D1、D\(_{2}\)上的高频信号幅度相等即UD1m=U\(_{D2m}\)如图6a；f＞fo时，ф＜0，1;2U\(_{2}\)和U·3间的相角为90°-ф，则有U\(_{D1m}\)＞UD2m如图6b；f＜f\(_{o}\)时，ф＞0，\(\frac{1}{2}\)U·2和U·\(_{3}\)间的相角为90°+ф，则有UD1m＜U\(_{D2m}\)如图6c，如此，就将U·2与U·\(_{3}\)间相位的变化转换成 U·D1和U·\(_{D2}\)幅度的变化，完成了相幅转换过程。

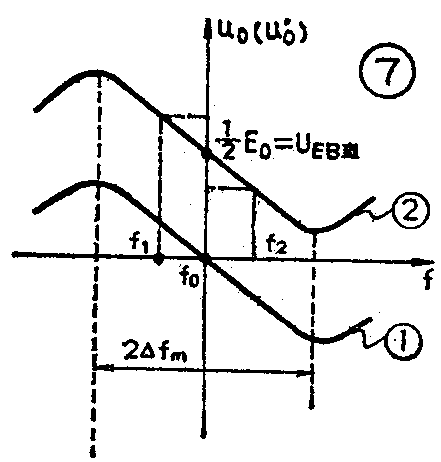
有了上述两个转换过程，再将U\(_{D1}\)和UD2的幅值变化由上下两个检波器差动检出，就达到了对调频信号的解调（即鉴频）目的。差动输出过程可由图2说明：D\(_{1}\)中检波电流的平均分量iD1是按点划线的方向经过地点（R\(_{5}\)、C3、C\(_{4}\)对15Hz以上信号呈现惰性）向负载电容C5充电，形成电压U'\(_{BE}\)；而D2中检波电流的平均分量i\(_{D2}\)是沿虚线方向对C5充电，形成电压U'\(_{EB}\)。由于在C5上两个充电电流的方向相反，所以输出电压U\(_{EB}\)=U'EB-U'\(_{BE}\)；又由检波器的传输特性可知：U'BE正比于U\(_{D1m}\)，U'EB正比于U\(_{D2m}\)，所以UEB亦正比于（U\(_{D2m}\)-UD1m）。当f=f\(_{o}\)时，UD2m=U\(_{D1m}\)，则输出交流电压（低频）UEB一U'\(_{o}\)=O；f＞fo时，U\(_{D2m}\)＜UDlm，则U'\(_{O}\)=UEB＜O；f＜f\(_{o}\)时，UD2m＞U\(_{D1m}\)如图6则U'O=U\(_{EB}\)＞O；由此可定性画出该电路的鉴频特性曲线如图7中曲线①所示，可见在一定的频偏范围（2m）内，U\(_{O}\)与f成线性关系。

1．直流电位关系式U\(_{EB直}\)=\(\frac{1}{2}\)UAB直的建立

由图1可知，该电路的输出电压U'\(_{O}\)自电感线圈L2的中点，经L\(_{3}\)和电阻R2由E点取出，B点接地，上、下两个检波电路只有一个负载电阻R\(_{5}\)，这就构成了该电路输出的不对称形式，使得电路在f=fo时，输出端E点对地的直流电位不为零。另外，为形成D\(_{1}\)和D2的直流通路，两个检波二极管是反向连接的；更为重要的是在A、B两端并接了大电容C\(_{4}\)（C4=10μf，因电解电容C\(_{4}\)对高频滤波特性较差，所以并联C3以完成对高频信号的滤波作用），与负载电阻R\(_{5}\)一起组成时间常数达0.22秒的RC网络。在检波过程中，这个RC电路对寄生调幅干扰及音频调制信号呈现很大的惰性，至使A、B两端电压UAB在动态平衡时（指两个检波器的充放电达到动态平衡，此时检波电流中的直流分量几乎均降落在A、B两端）达到恒定值，相当于一个电池E\(_{O}\)（UAB=E\(_{O}\)，见图1）加在A、B两端。我们画出该鉴频器正常工作时直流电位关系示意图如图8（a）所示，可以看出，EO的存在相当于给两个检波二极管D\(_{1}\)、D2一个恒定的反偏压，使D\(_{1}\)、D2的导通角θ\(_{1}\)和θ2均小于180°。因为D\(_{1}\)、D2参数对称，且R\(_{3}\)=R4，L\(_{1}\)'=L2"=12L\(_{2}\)（见图8（a），显然EO给D\(_{1}\)、D2提供的反偏压相等（（U\(_{DI反}\)=UD2反），产生的反向电流相等（I\(_{D1反}\)=ID2反），其反向电阻也相等（R\(_{D1反}\)=RD2反）。当忽略L\(_{3}\)及R2上的直流压降后，我们可将图8（a）等效成图 8（b）的形式（图中r\(_{2}\)'=r2"为L\(_{2}\)／2的等效损耗电阻），显见这是一个1;2等分的分压电路，EO与U\(_{EB}\)间存在\(\frac{1}{2}\)的关系即UEB直=1;2E\(_{O}\)=\(\frac{1}{2}\)UAB直。由于这一关系的存在给电路调整带来了很大方便，同时使得调制信号为零时（即f=f\(_{O}\)），鉴频器输出（指E点对地）不为零，考虑了这个直流电位的鉴频特性曲线如图7曲线②所示。

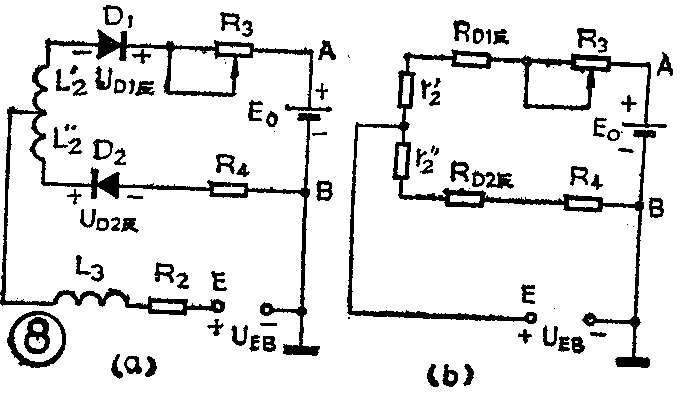
必须强调指出，上述关系式是在鉴频器正常的动态工作状态下建立的。E\(_{O}\)并不是一个真正的电池，而是一个与鉴频器工作状态密切相关的参量，当电路工作在较佳状态时，UAB=E\(_{omax}\)，UEB=12E\(_{omax}\)。因此，我们可以直接利用这一直流电位关系进行电路调试。

2.U\(_{EB直}\)=\(\frac{1}{2}\)Eomax是电路工作状态最佳的标志。

我们说电路调整好了，就是说电路工作在最佳状态。本电路最佳状态的标志是初、次级谐振回路均谐振在调频信号的中心频率f\(_{o}\)上。即调整初、次级谐振回路电感线圈的磁心，改变回路电感量，使得\(\frac{1}{2π}\)·1;\(\sqrt{LC}\)=fo(f\(_{o}\)=6.5MHz)。调整中我们不用专门测量仪表，而是用三用表和UEB直=12E\(_{omax}\)的关系式。当初级回路调谐时，UAB直达到E\(_{O}\)的最大值Eomax；当次级回路调谐时，U\(_{EB直}\)达到Eomax的二分之一。这可以解释如下：

因为U\(_{AB}\)=EO是由于检波电流中的直流分量在惰性元件C\(_{4}\)两端形成电压降的结果，所以UAB正比于U\(_{Dlm}\)、UD2m（如图6所示），U\(_{D1m}\)和UD2m又正比于U\(_{2m}\)、U3m，其中U\(_{2m}\)和U3m的大小均由U\(_{1m}\)的大小所确定，归根到底，UAB取决于U\(_{1m}\)（下标带m指信号幅度）Ulm达到最大值，U\(_{AB直}\)也达到最大值。而只有在初级回路谐振在fO时，U\(_{1m}\)才得到最有效的传输。如图9曲线①所示（注意图9只是并联谐振回路幅频特性的示意图，曲线②和③为回路失谐的情况），此时UAB直=E\(_{omax}\)。

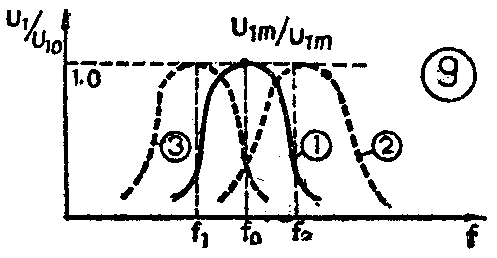
对于次级回路，前面已经阐明，只有在回路谐振于f\(_{o}\)时，U·1与U·\(_{2}\)才互相垂直，UD1m=U\(_{D2m}\)（如图6（a）所示），使得D1，D\(_{2}\)的导通角相等，图8（b）的直流电位关系才成立，即有UEB直=12E\(_{omax}\)成立。这一点还可从鉴频特性曲线（图7曲线②）已直接看出：当次级回路失谐即谐振频率为 f1（小于f\(_{o}\)）或f2（大于f\(_{o}\)）时，则对应的UEB大于1;2E\(_{o}\)或小于\(\frac{1}{2}\)Eo。

必须指出，由于初、次级回路各种寄生参量的相互影响及耦合回路之间的阻抗反射作用，使初、次级回路的调整互相受到牵连，所以在调整时需反复进行几次，方能达到较好效果。

具体调测方法如下：调试时利用电视台的调频信号（即电视机中经过图象检波后从预视放送到电视伴音通道的伴音信号），首先调整鉴频器前级中放谐振回路与初级谐振回路（即B\(_{1}\)磁心），使UAB电压达到最大值（用三用表直流电压档在A、B两点监测），然后，调整鉴频器次级回路（即B\(_{2}\)磁心）及电阻R3（调整R\(_{3}\)可补偿两个检波支路的不平衡），使得UEB=12U\(_{AB}\)（用三用表直流电压档在E、B二点监测），上述过程反复进行2—3次，就能达到较佳工作状态。

这种方法对调频广播接收机中的不对称比例鉴频器的调试同样适用，只是注意设计时使鉴频器初、次级回路的谐振频率与调频波的中心频率一致。

当然，在实验室条件下，用扫频仪观测并调整鉴频特性曲线（即S曲线）或用高频信号发生器及晶体管毫伏表逐点测试并调整S曲线，使其达到性能指标，会更直观一些。但本文所述方法较为简单。(姚卫东)