(闻芒)正弦交流电还有一种表示方法,叫做复数表示法。我们在前文曾介绍过正弦量可以用旋转着的矢量来表示,由于在数学上矢量是可以用复数表示的,所以正弦量也可用复数表示。这种表示方法是把正弦量记作复数这个“数”的表示式,所以用来计算电路问题时就成为对复数这个“数”的代数运算过程,而复数的运算比起三角函数或几何运算来要简单得多,所以这种表示法得到了广泛的应用,是研究交流电路不可缺少的工具。本文将集中讨论这种方法。
什么是复数
在数学或者某些工程问题的计算中,有时会遇到求解方程而得不到实数解的情况。例如,求方程x\(^{2}\)+36=0的解。这里,其根应当是X=±\(\sqrt{-}\)36。我们知道,在实数范围内任何数的平方都不为负值,所以负数是不能开方的。为了使这类问题得到解答,早在16世纪时人们就引入了一个新的数,叫做虚数,并且令虚数的单位为-1,记作i=\(\sqrt{-}\)1。这样,-36就可写作:6\(\sqrt{-}\)1=6i,上述方程的解就是X=±6i,即,x是等于6个虚数单位的一个虚数。
如果一个数既包括实数又包括虚数,它就可认为是由两部分所组成:即实数部分a和虚数部分bi,在数学上把这样的数叫做“复数”,并且记作a+bi,请注意,这里的“+”并不表示相加的意思,它只是一个符号,表示复数包括a和bi这样两个部分而已。例如:复数3+2i、\(\frac{1}{2}\)+2;3i等等。其实数部分分别是3和\(\frac{1}{2}\),虚数部分分别是2i和2;3i。
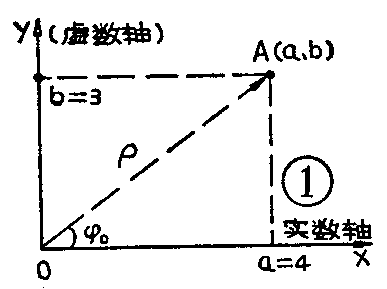
一个复数,常用大写字母上加“·”来表示,如复数A·=a+bi,U·=c+di等等。其中实数部分(如 a、c)简称实部,虚数部分(如bi,di)简称虚部。b,d,称作虚部的系数,而且实部和虚部的系数本身也都是实数。在数学上,表示一个复数,也可和表示其它函数一样,用平面直角坐标系中的一点来表示。这时,模座标轴(X轴)表示实数部分,纵座标轴(y轴)表示虚数部分,纵轴的单位长度是i=\(\sqrt{-}\)1。例如,有一个复数A·=a+bi=4+3i,在直角坐标平面上就可用一点A代表它,A点的坐标分别是a= 4,b=3,如图1。这种用来表示复数的座标平面叫做复平面,其特点是纵轴的单位长度是i。可见,在复平面上的任何一点,都唯一地代表着一个复数。
矢量与复数的关系
为着最终找出正弦量—矢量—复数三者之间的关系,以便用复数表示正弦量,先讨论矢量与复数的关系。在图1中,连接原点o与A并把o看作是oA的起点,A是终点,则oA→是一个有方向的矢量。设oA→的长度为ρ,与oX轴的夹角为ф0,显然,A点将唯一地决定着矢量oA→,所以这个画在复平面中的矢量oA→可以用A点在复平面中所唯一代表着的复数来表示。因oA→在x轴上的投影为a,在y轴上的投影为b,(当然,oa和ob也是有方向的矢量,即oA→的两个分量)那么,代表矢量oA→的复数当然就是A·=a+bi。由几何关系不难看出,ρ=\(\sqrt{a}\)\(^{2}\)+b2、a=ρCOS0、b=ρsin0及0=arctg\(\frac{b}{a}\)对于代表矢量oA→的复数A·,称ρ为此复数的模,烁词姆恰S缮鲜龉叵敌闯龈词娜呛硎臼骄陀校
A·=a+bi=ρcos0+iρsin0
在数学中,有所谓欧拉公式,证明了上式又可写成指数形式即:
A·=ρcos0+iρsin0=ρei0(证明从略)
所以复数也可写作A·=ρ·e\(^{i}\)0
如果矢量oA→在复平面中的位置并不是固定不变的,而是以角速度ω=\(\frac{2π}{T}\)绕原点o从上述初始位置0作逆时针的匀速旋转运动,T为旋转周期;则在时间t时它就旋转了角度豻,即该矢量在任何时间t时所处的位置oA→1应取决于角度430=ωt+0,见图2。如果用复数来表示这个矢量,显然就应当是A·\(_{1}\)=ρ〔cos(ωt+0)+isin(ωt+0)〕或者写成指数形式A·1=ρ·e\(^{i(ωt+}\)0)
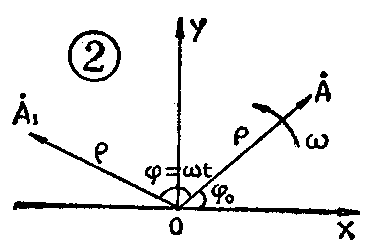
正弦量的复数表示法
我们已经知道,正弦量可用旋转矢量表示,上面又说明了旋转矢量可用复数表示,所以正弦量必然也可用复数表示。这就是正弦量的复数表示法。正弦量、矢量、复数三者的对应关系,可以列表如下:
正 弦 量 最大值 初 相 频 率
旋转矢量 长 度 起始相角 转 速
复 数 模 辐 角 辐角的变化频率
由此可见,描述一个正弦量所必需的三个要素,在复数中都有一定的数学量与之一一对应。若用复数表示正弦量,就是:复数的模代表正弦量的最大值、复数的辐角初始值代表正弦量的初相(角),复数辐角随时间的变化量代表正弦量的相角变化量。举例来说:设已知一正弦电流为i(t)=I\(_{m}\)sin(ωt+0)则表示此电流的复数(称作复电流)便是:
I\(_{m}\)〔cos(ωt+0)+jsin(ωt+0)〕
写成指数形式为:I\(_{m}\)e\(^{j}\)(ωt+0)
这里,虚数单位的符号改用j来代替i,以防和瞬时电流的表示符号混淆(在电学问题中都是这样表示的)。同理,如果有一正弦电压u(t)=U\(_{m}\)sin(ωt+0),其复数表示式就是:
U\(_{m}\)(cos(ωt+0)+jsin(ωt十0)〕=Ume\(^{j}\)(ωt+0)
上述电流电压的复数表示式还可写成
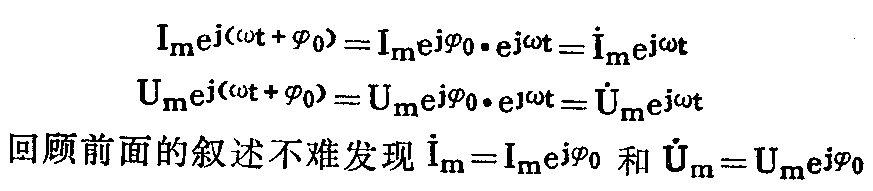
都是当t=0时即不考虑随时间的变化关系时的固定复数(或者,考虑到矢量—复数的对应关系,就是代表矢量初始位置时的复数),而e\(_{jωt}\)只是表明复数与时间的关系或者说与此复数对应的矢量的旋转特征,所以称ejωt为旋转因子。正如在矢量表示法中已谈过的,讨论几个同频率ω的正弦量之间的相互关系时,可不去考虑旋转问题,而只研究初始状态的相对关系,所以在用复数表示正弦量时也同样不必考虑e\(_{jωt}\)一项。用复数表示正弦交流电并进行计算时也是只用初始状态(t=0)的复数表达式即可。上例电流电压的复数表示式也就简化为I·m=Im\(^{ej}\)0和U·m=U\(_{m}\)ej0了。
需要说明的几个问题
(1)在复数麦示法中,真正代表正弦量瞬时值的,是复数中的虚部系数,而不是整个复数表示式,所以如果有正弦量(例如电流)

所以任何正弦量用复数表示时,如果乘以j,就表示将与此复数对应着的矢量(即在矢量法中代表该正弦量的那个矢量)逆时针旋转90°(前进90°);乘以-j,就相当于将与此复数对应的矢量顺时针旋转90°(后退90°)。这一点,在表示电感电容等元件上的电压电流间的相互相位关系时,是很有用的。例如,电感上的电压超前于电流90°,用复数表示这种关系就是:
U·\(_{L}\)=jωLI·L
电容上的电压滞后于电流90°,则
U·\(_{C}\)=-j\(\frac{1}{ωC}\)I·c
其中:U·\(_{L}\)、U·C,分别为电感和电容上的复中压;
I·\(_{L}\)、I·C,分别为电感和电容上的复电流。
(3)无论是前文中的矢量表示法还是本文的复数表示法中,矢量长度或复数的模都被认为是正弦交流电的振幅值如Um,Im等,实际上正弦交流电常用有效值计算,所以为计算方便,矢量长度或复数的模也可用有效值表示,这时,符号就不加下标m而写成U→I→或U·I·,以此计算,其结果亦为有效值。因为有效值=1\(\sqrt{2}\)振幅值,只差一个常数,故原理不变。
(4)在计算电路问题时,复电压和复电流的比值\(\frac{U}{·}\)I·=Z叫做复数阻抗,简称复阻抗.在形式上此式与欧姆定律一样,所以是复数形式的欧姆定律。这里的Z,是在计算时两个复数U·和I·相除的结果,虽然也是一个复数,但并不同于正弦量用复数表示的概念,阻抗本身也不是一个正弦量,所以Z只是计算过程中出现的一个复数计算量,因而特别以大写字母z表示,而不再加“·”,以示区别。复阻抗表示着电路中电压电流间的关系,只取决于元件的参数,所以是一个复数形式的常数,电路的阻抗数值就是它的模值。而它的辐角则表示电压电流间的相对相位关系。
(5)我们所介绍过的各种表示正弦量的方法,都只不过是为了说明问题或计算上的便利而采取的“方法”;在波形图法中,正弦电流也只是说在导线或电路中正电荷随时间运动的多少和方向,在本质上它不同于具有时空概念的波动过程,波形图也仅仅能使电流变化的物理过程形象化,并不能说正弦电流就等于正弦波。同理,用旋转矢量或复数表示正弦量,也决不是说正弦量就等于旋转矢量或复数,这只是为了计算方便而采用的一种数学工具、一种数学表示方法。有时把复数表示法也叫做“符号法”就是这个道理,即,无非是借助复数作为一种表示正弦量的“符号”,以求计算上的方便面已。
(6)在用复数表示法进行电路计算时,交流电路的各种计算公式都可直接应用,只要在各物理量上注出复数标记,并遵循复数的运算规则即可。比如:
欧姆定律为\(\frac{U}{·}\)I·=Z
串联电路中各分电压之和等于总电压:
U·=U·\(_{1}\)+U·2+U·\(_{3}\)+……
并联电路中总电流等于各支路电流之和:
I=I·\(_{1}\)+I·2+I·\(_{3}\)+……等等。