交流电的表示方法

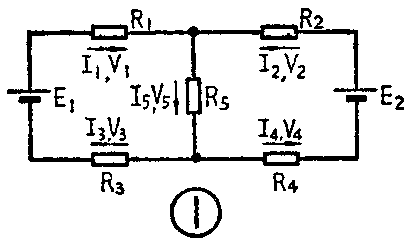
在分析电路问题时，常要进行必要的计算，而计算过程的第一步工作，就是如何把被计算的物理量如电压、电流、电动势等等确切地表示出来。对于直流电的问题，由于电压、电流、电动势等物理量的大小和方向都恒定不变，所以表示起来很简单，例如图1那样的直流电路，只需标明已知量如E\(_{1}\)E2I\(_{1}\)I2……V\(_{1}\)V2……等的数值大小，并用正负号（对E\(_{1}\)、E2）或箭头（对I\(_{1}\)I2……V\(_{1}\)V2……）标出其方向就可进行计算了。未知量（如I\(_{4}\)及V4）的方向可以假设，然后根据计算结果再判别实际方向，计算结果为正值时与原假设方向一致，否则相反。而对于交流电的问题，要确切地表示电压、电流、电动势等等被计算的量，只表明大小和方向这两个要素是不够的，因为交流电本身要复杂得多。

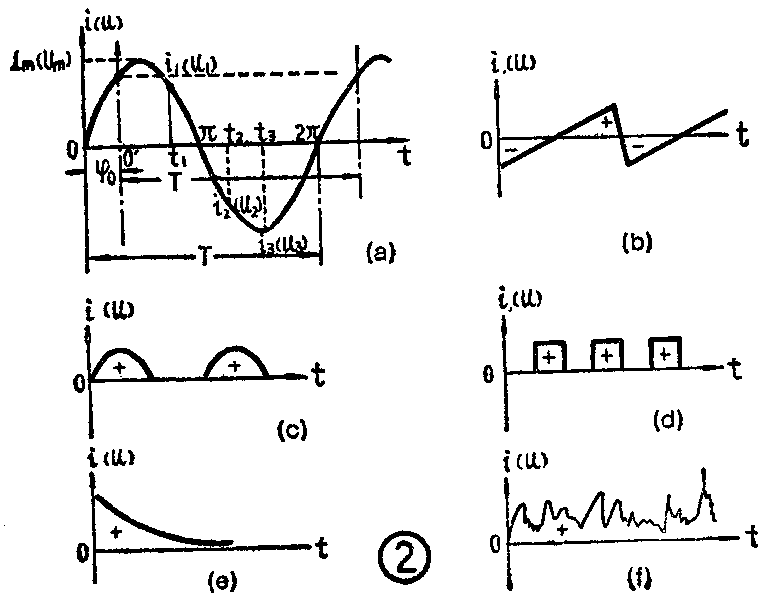
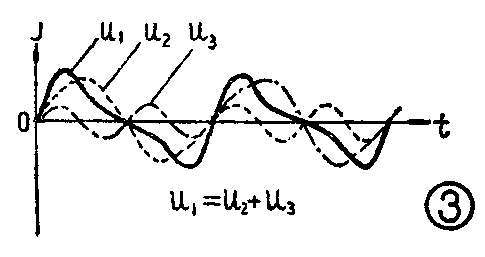
广义上的交流电，是指大小或方向在随时间变化着的电压或电流。其随时间变化的情况又可能是各种各样的。图2列举了几个交流电流（电压）的例子，它们可能有一定的规律性，如图2a、b、c、d、e，也可能没有规律性，如图2f。显然，只用数值大小和方向还不能确切地表示它们。但是，我们习惯上所说的交流电则是专指大小和方向都随时间按正弦规律变化的电流或电压（图2a），如220伏市电。其他非正弦电流或电压可统称为脉动电流或电压，也可依各自的特点分别称作锯齿电流（电压）（图2b）、脉冲电流（电压）（图2c、d）、指数电流（电压）（图2e）、随机电流（电压）（图2f）等等。当然，它们都是广义上的交流电。对于图2b、c、d、e等这类有规律性的物理量，从数学分析的结果得知，可把它们分解成多个频率和幅度各不相同的正弦量之和。这里，试举一个简单的例子：如图3中的非正弦电压u\(_{1}\)，就可分解为频率和幅度各不相同的两个正弦电压u2和u\(_{3}\)之和。即，u2和u\(_{3}\)逐点相加就是u1。其他各复杂波形也是一样，只是要由更多的正弦分量才能合成罢了。所以，在分析计算有规律性的脉动电流（电压）时，就可分别分析每一个正弦分量，然后再求其总和结果，这样就把问题大大简化了。分析无规律性的随机电流（电压），按理必须用概率和统计的方法，这是很复杂的，所以也常常近似地找出某种规律性，然后也按上述方法作近似分析或计算。

这样，无论是正弦交流电还是非正弦交流电，在电路中进行分析计算时，就都可归结为简单正弦交流电的计算了。所以正弦交流电的表示和计算方法就成了分析交流电路的基础。那么，怎样才能确切地表示正弦交流电呢？

要描述一个交流电流或电压，最直观的方法就是画出它们的大小与方向随时间变化的图形，如图2那样。这种以纵轴表示电流（或电压）的大小，以横轴表示时间的直角坐标系中，表示电流（电压）随时间变化情况的图形就叫波形图。显然，无论是否为正弦量，都可用波形图来描述。而图2a所示的正弦电流（或电压）的波形图是一个周期性重复的过程，重复周期为T。这个正弦量的最大可能值（简称最大值或振幅值或幅值）通常用I\(_{m}\)（电流）Um（电压）表示。任何瞬时的数值（称瞬时值）就是对应着这个瞬时的正弦曲线上的点的纵坐标。通常用小写字母表示，如电流i，电压u。图中对应着瞬时t\(_{1}\)、t2、t\(_{3}\)……的电流（或电压）瞬时值就是i1、i\(_{2}\)、i3……（u\(_{1}\)、u2、u\(_{3}\)……）。因为正弦函数变化一周的时间是周期T，而所谓变化一周，就是变化了360°（2π弧度）又回到初始数值的时间，所以在单位时间内变化的弧度数就是\(\frac{2π}{T}\)。当时间轴的坐标原点0（t＝0）如图那样选择时，在任何时间t时，正弦函数变化的弧度数就是2π;T·t，而对应着时间t的正弦函数数值（瞬时值）便可写为：

这是以正弦电流为例。式中\(\frac{2π}{T}\)·t显然代表在时间t时正弦函数对应的角度，称为相角。如果在分析时我们并未把t=0的坐标原点选在正弦函数数值为零的地方，而是选在了0＇点（纵坐标在点画线处），或者说，在研究的初始瞬时（t=0＇），正弦量并不为零，也就是在t=0＇时，正弦函数已经具有了一个角度0，因此在时间t时，函数值就应当是

这里，0就称作起始相位角或简称初相（角）。

这样，一个正弦量，只要知道了它的幅值，周期，和初相，就可以确切地写出它的数学表示式来。并且，可以据此求出任何瞬时的数值大小。有了这些瞬时值当然就完全描述了正弦量本身。说得更明确些，要确切描述一个正弦量，不管用什么方法，都必须能表明幅值，周期和初相这三个要素才行！

用波形图表示交流电（包括非正弦交流电）是很形象的，也便于两个以上波形的定性观察与比较，所以在测量中这种表示方法常被采用，例如用示波器观察波形，并从刻度上读出数值（幅值，周期）等。在电视机电路图中也常给出不少波形图并标出数值以便监测调整。可惜的是，这种方法用来进行计算就太繁琐了，一方面画图难以准确，又很麻烦；另一方面，如作电路计算，即使是简单的加减运算，也必须将被运算的波形逐点相加减，然后求出结果，这显然是不可取的。更不用说复杂计算了。

上述的三角函数表示式能够明确而方便地描述正弦交流电的特征（幅值、周期或频率、初相），这是它的优点，但是用三角函数表示式进行正弦交流电的运算，也是相当复杂的，因此实际上也很少采用。为了解决能够方便地计算正弦交流电的问题，就需要寻求正弦交流电的新的表示方法。

如上所述，正弦量是一个简单的周期性重复的过程。它和物理上一个匀速圆周运动的点所具有的运动规律极为相似。能否借后者表示正弦量呢？让我们看看下述情况：

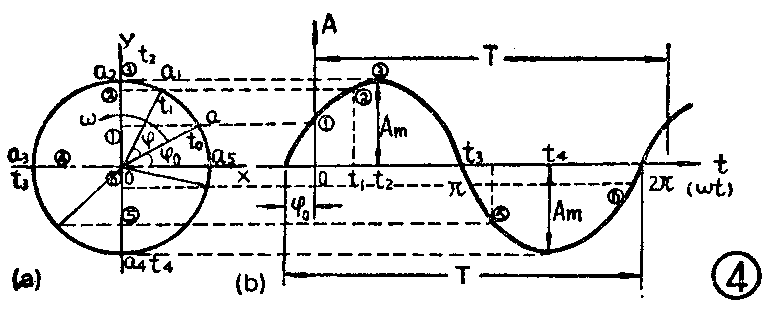
设图4a中的点a在直角坐标平面中从与ox轴夹角为0的初始位置绕圆心O作逆时针圆周运动，半径oa=Am。如果a点在某一瞬时所处的位置为a\(_{1}\)，则a1的位置将只取决于oa\(_{1}\)与oa之间的夹角或者说a从初始位置旋转了角度到达a1点。oa\(_{1}\)与ox轴的夹角便是430。若圆周运动进行一周的时间（周期）为T，则转过的角度是360°，即2π弧度。单位时间内转过的角度（称为角速度ω）便是ω=\(\frac{2π}{T}\)弧度。如a点运动到a\(_{1}\)的时间为t1，则豻\(_{1}\)，oa1与ox轴的夹角应是0=ωt1+0。这里，0是决定a\(_{1}\)点位置的角度，称相位角（简称相位或相角），0决定着a点的初始位置，故称初相（角），类推下去，则a点运动到a\(_{2}\)时，0=90°，到a\(_{3}\)时0=180°，到a\(_{4}\)时0=270°，到a\(_{5}\)时0=360°……。此外，因为oa是从o→a有方向的量，所以称为矢量（长度为A\(_{m}\)）。这样，只要知道了Am，0和ω，（或周期T=2π;ω，或频率f=\(\frac{1}{T}\)=ω;2π）这三个参数，就完全决定了a点在任何瞬时的位置。同时，再看旋转着的矢量oa在纵轴oy上的投影：设oa的投影为o①，oa1的投影为o②，oa\(_{2}\)的投影om，oa\(_{3}\)的投影为零，oa4的投影便为-A\(_{m}\)，这些变化着的投影若用oy表示，则由几何关系可知：

即，投影oy随时间按正弦规律变化着。如果把oy值与对应的时间t\(_{0}\)、t1、t\(_{2}\)……之间的关系逐点移画到图4b的直角坐标系中去，得到的当然是一个正弦曲线。这是一个很有价值的结果，它表明，旋转矢量oa的特征反映了正弦函数的所有特征，即，为确切表示一正弦量所必需的三要素都可从旋转矢量中找到：矢量长度Am是对应正弦量的振幅，矢量的初相0是对应正弦量的初相，矢量旋转的角频率ω＝\(\frac{2π}{T}\)又正是对应正弦量的角频率。进一步说，旋转矢量oa在纵轴上的投影oy，又恰与正弦函数的瞬时值一一对应！所以，我们完全可以用一个旋转矢量准确无误地代表一个正弦量（也仅仅是借它来“代表”而已！），这就是正弦函数的所谓矢量表示法。通常，一个矢量是用其长度加箭头来表示的，例如上述矢量oa便表示为A→m。

那么，怎样用旋转矢量来代表正弦交流电流或电压呢？我们举个正弦电压的例子来具体说明这种表示方法：设已知一个正弦电压

如用旋转矢量来表示它，则代表它的旋转矢量U→\(_{m}\)的长度就是Um，旋转矢量的初相就是0，旋转矢量的旋转角频率就是ω=\(\frac{2π}{T}\)（即上式中的ω）。在直角坐标平面中画该旋转矢量，就是图5。可见，旋转矢量U→m在纵轴上的投影正是上式正弦电压的瞬时值

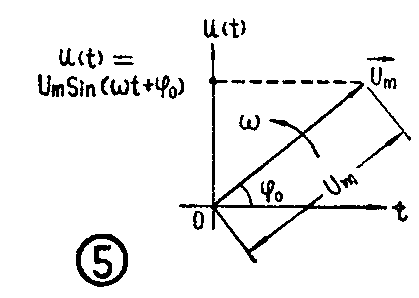
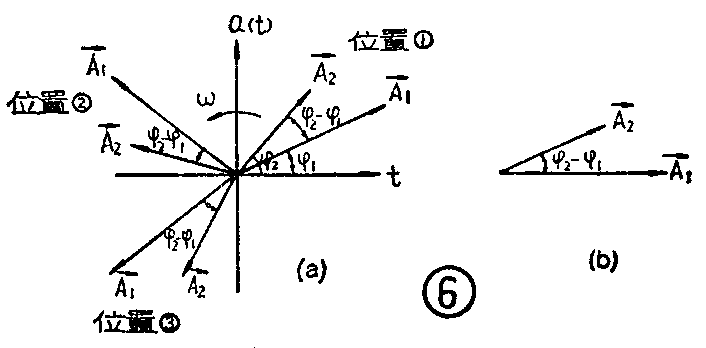
如果要用旋转矢量同时表示两个以上同频率的正弦量，则代表它们的旋转矢量的旋转角速度便相同，它们之间的相互位置关系将只取决于初始状态时的初相（角）之差，而在旋转过程中此相互关系始终不变。例如：图6a中的两个同频率ω的矢量A→\(_{1}\)→2，初相差为2-1，当由位置①旋转到位置②、位置③时其相互关系依然不变。所以，当我们只研究几个同频率旋转矢量之间的相互关系时，完全不必再画坐标系统，而只以其中一个矢量为参考基准，画出它们的相互关系就可以了。如图6b那样。

不言而喻，既然可以用矢量代表正弦量（如正弦电流，电压）当然就可以用矢量去计算它所代表的正弦量。若要进行两个以上矢量之间的加减运算，当然可用数学上矢量求和（或差）的平行四边形法则去求解。不妨举个简单的例子：

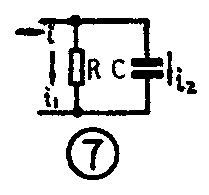
求图7中简单RC并联交流电路中的总电流i：

先画一矢量I→\(_{1m}\)，取其长度为I1m=3（见图8）并以此作为参考矢量，逆时针旋转90°，画出矢量I→\(_{2m}\)的相对位置，并取其长度I2m=4，显然I→\(_{1m}\)和I→2m就分别代表正弦电流i\(_{1}\)和i2的对应矢量，二矢量I→\(_{1m}\)、I→2m之和可用平行四边形法则求出，在图8中对角线矢量I→\(_{m}\)=I→1m＋I→\(_{2m}\)便是。当然，这个和矢量I→m一定会反映着所求和电流i的一切特征。I→\(_{m}\)的幅值是Im，由图8中的几何关系不难得知I\(_{m}\)=5，I→m与参考矢量I→\(_{1m}\)之间的夹角可由几何关系写出rctg\(\frac{4}{3}\)≈53°8'。即，和矢量I→m所代表的和电流

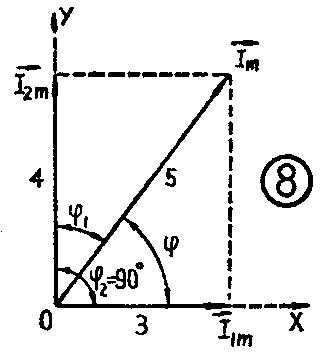
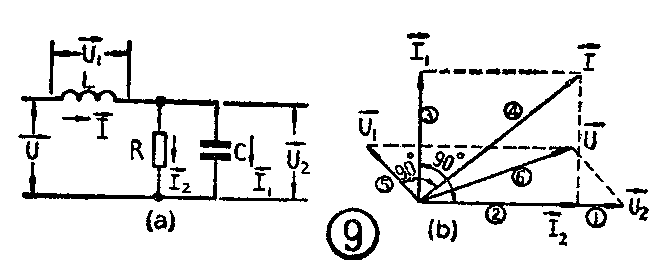
这里，矢量图还表明了合成矢量I→\(_{m}\)与I→1m、I→\(_{2m}\)之间的相位关系，即I→m超前于I→\(_{1m}\)，I→m滞后于I→\(_{2m}\)1角（即，i超前于i\(_{1}\)，而滞后于i2牵Ｓ纱丝杉庵址椒ū硎菊业缌骰虻缪怪涞南嗷ス叵担中蜗笄逦绕湓诒砻鞫喔鍪噶考涞母丛酉辔还叵凳保飧鲇诺愀油怀觥１热纾枰砻魍9a电路中各电流、电压间的相互关系，考虑到电感上电压超前于电流90°，电容上电流超前于电压90°，电阻上电压与电流相位相同这个前提，不难画出各电流电压间的矢量关系图（见图9b）。设取U→\(_{2}\)作参考矢量，画图步骤如下：先画矢量U→2（这里用的是有效值），长度为U\(_{2}\)；再画电阻上的电流I→2（与U→\(_{2}\)同相），长度为I2；再画电容上的电流I→\(_{1}\)，超前于U→290°（逆时针旋90°），长度为I\(_{1}\)；再用I→1、I→\(_{2}\)求出和电流失量I→（平行四边形法则，I→为对角线），再画电感上电压U→1，超前于I→90°（自I→逆时针旋转90°），长度为U\(_{1}\)，最后，求总电压U→：利用平行四边形法则，以U→1、U→\(_{2}\)为边，作平行四边形，得对角线矢量即为总电压矢量U→（∵U→＝U→1＋U→\(_{2}\)），该作图步骤在图9b中标示如①～⑥。显然，图9b所示的矢量图使得电路中各处电压和电流之间的相互相位关系一目了然，因此，当作定性研究，尤其是分析电压、电流的相位关系时，大都采用这种方法，比如用来分析频率检波电路（鉴频器）的工作情况时，几乎都采用这种方法。

至于用矢量图作电路问题的理论计算，则由于一方面作图误差大，难以准确；另一方面矢量的复杂几何运算也相当复杂，所以只宜于在简单线性电路中作正弦量的简单加减运算，而不用来作复杂计算。大量的计算工作中表示正弦电流电压等却是采用我们将要介绍的更简单的复数表示法。(闻芒)