随着大功率收音机及扩大机的不断增多,在居住环境比较拥挤的地方出现了一种新的“公害”——“闹声”公害。一些音乐爱好者欣赏音乐时为了追求足够的高音、低音,拼命将音量开大,这就影响了周围邻居的休息和学习。不但如此,欣赏者本人在强大的声压场环境里,时间长了也会出现听觉疲劳和烦燥情绪。因此,如何解决小音量情况下得到高、低音丰满的音质就成为一个非常现实的问题。
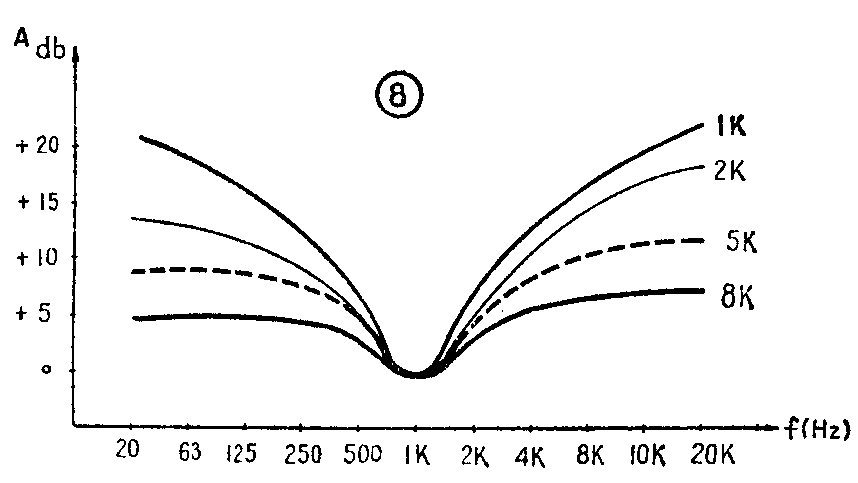
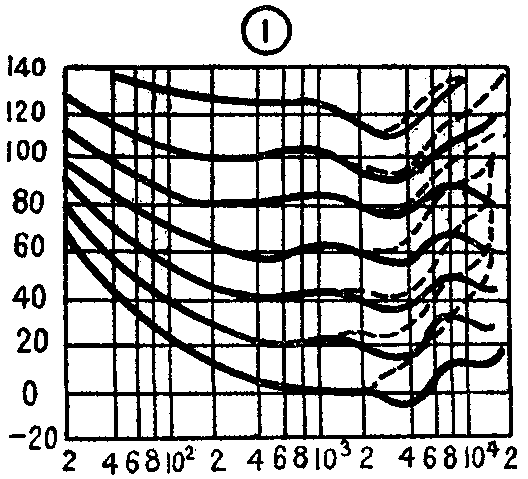
通常音量的大小与频响是无关的,但人耳听觉的频响特性对音量大小却有很大关系。随着音量由大到小,耳朵对高、低音的灵敏度会不断减弱,图1是人耳的听觉频率响应曲线。图中的实线表示青年人的听觉特性,虚线表示老年人的听觉特性。从图中可以看出,1000Hz的声音如果是20dB声压,则100Hz需再提高20dB声压(即40dB);8000Hz需再提高16dB声压(即36dB),才能在青华人的听觉上感到它们的响度相等。如果是老年人,8000Hz需再提高30dB(即50dB)声压才能有等响度感觉。如果中音1000Hz声伍提高到60dB,则100Hz只提高12dB声压;8000Hz只提高5dB声压就能在青年人的听觉中产生等响度感觉了。由此可见,声压越高则曲线的高、中、低音部分越趋平坦,需要达到等响度效果的提升量也越减小,这就是音量越开大,高、低音感到越丰满的原因。当然,人耳频响特性是无法改变的,要解决这个问题只能在电路上采用等响度补偿电路。由于响度补偿须随音量大小而变化,所以响度补偿应加在音量电位器上。响度补偿电路有多种,这里只介绍两种最常用的电路。
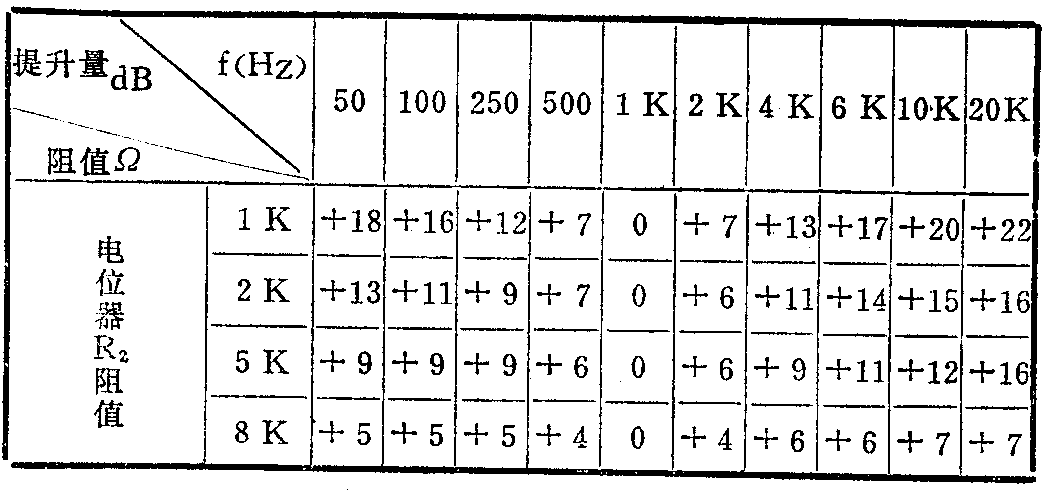
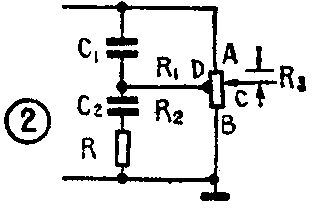
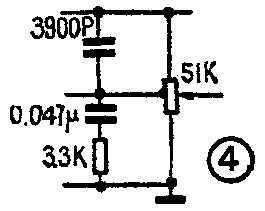
1.抽头电位器法像图2那样,在音量电位器上抽一个头。该抽头位置一般取在阻值的\(\frac{1}{5}\)~1;2范围内(离地端)。假设音量电位器抽头D上部DA阻值为R\(_{1}\), D下部DB阻值为R2,滑动脚C至A端阻值为R\(_{3}\)。R1和C\(_{1}\)组成高音提升网络。R、C2组成低音提升网络。当电位器滑动臂C点转到A端时(即音量开到最大),信号直接输出,R\(_{3}\)=0,此时高、低音提升网络均不起作用,其频响为一直线。随着C点向D点接近(音量逐渐减小)CD两点间阻值减小, R1、C\(_{1}\)高音提升网络和R、C2低音提升网络的作用逐渐增加。当C点与D点重合时,高、低音提升量达到最大,C点再继续向B点靠拢时,基本上保持这个提升量。高音提升的转折频率为f\(_{1}\)=1/2πR1C\(_{1}\),低音提升的转折频率为f2=1/2πRC\(_{2}\)。高音提升网络是一个RC高通网络,因此它的最大提升量约为每倍频程6dB,而低音提升网络实际上是一个高音衰减电路(如图3),频率越低C2容抗越大,衰减量越小,因此它的最大提升量与并联在RC\(_{2}\)旁的R2阻值有关。假设最大提升量为A,则R=R\(_{2}\)/A-1。下面举一个实例求算各元件值。例如使用51KQ音量电位器,抽头为\(\frac{1}{5}\),则R1=41KΩ、R\(_{2}\)=10KΩ。设1000Hz为高、低音转折频率,则C1=1/2πfR\(_{1}\)=1/6.28×1000×41×10\(^{3}\)≈3900pF。我们取低音最大提升量A=4,则R=R2;A-1=1044-1=3.3KΩ,C\(_{2}\)=1/2πfR=1/6.28×1000×3.3 ×10\(^{3}\)≈0.048μF完整电路如图4。
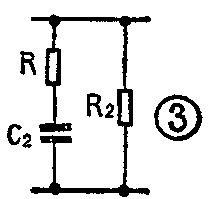
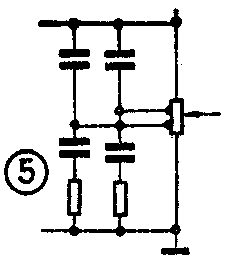
抽头电位器响度补偿的补偿量与抽头位置有关、抽头位置高补偿作用早,但提升量小,抽头位置低,补偿量大,但作用晚,因此可采用两个抽头办法来解决作用早与补偿量大的矛盾。图5就是一个双抽头电位器响度补偿电路,其工作原理及元件计算方法均与上述相同,此处不再赘述。抽头电位器法虽然效果很好,但市场上抽头电位器不易买到。
2.LC响度补偿法 LC补偿法仅需像图6那样,在普通音量电位器上并联一个LC网络就能得到理想的补偿效果。这种方法材料容易购买,制作简单,容易在现成的放声设备中增加响度补偿,而且对不同阻值的音量电位器(4.7KΩ~100KΩ)均能使用。
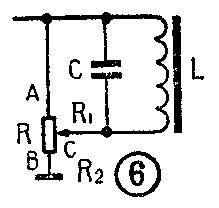
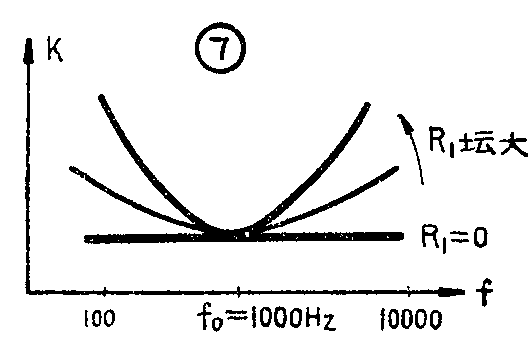
这种电路的原理是这样的:LC构成谐振回路,谐振频率为中频(1000Hz)。并联谐振时阻抗很大,偏离谐振点越远阻抗越小,因此LC回路对高、低音阻抗均比 1000Hz时阻抗低,所以得到提升。LC并联在R\(_{1}\)两端,当R1=0时(即音量开到最大)LC回路被短路,无提升作用,随着C点下移, R\(_{1}\)阻值增大,LC回路Q值逐渐增大,诸振曲线趋向尖锐,高、低音提升量也逐步增大(如图7)。
元件计算方法如下:考虑到加上响度补偿之后对中频(1000Hz)影响不要太大,应使回路对1000Hz的阻抗大于原音量电位器阻值的2倍,即ωL=2R(图6)式中ω=2πf\(_{0}\), f0为转折频率,这里取f\(_{0}\)=1000Hzf0=1/2π\(\sqrt{2}\)\(^{L}\)C,如果电位器阻值为10KΩ则L=2R/ω=2R/2πf\(_{0}\)=2×10×1032×3.14×1000≈3亨C=1/(2πf0)\(^{2}\)L =1/(2×3.14×1000)2×3≈0.01μF
电感线圈可用E19×8矽钢片作铁芯,用φ0.01毫米漆包线绕1700圈。LC响度补偿电路的信号源要求是等压源,也即信号源内阻应很小,否则影响提升量。提升量的近似计算方法如下:
A=\(\sqrt{1}\)+(R\(_{1}\);Z)\(^{2}\);1+(R2R\(_{1}\)Z(R1+R\(_{2}\)))2
式中Z可以是谐振回路的感抗,也可是谐振回路的容抗。低频时由于感抗小于容抗(ωL<\(\frac{1}{ωC}\))容抗可忽略,此时可用ωL代替Z;高频时容抗小于感抗(ωL>1;ωC),感抗可忽略,此时可用1/ωC代替Z。另外R=R\(_{1}\)+R2,R是电位器阻值。所以对于10KΩ电位器,在100Hz时的提升量为:
A=\(\sqrt{1}\)+(8;2)\(^{2}\);1+(\(\frac{2×8}{2×(8+2)}\))2≈3.8倍即11dB。
这里假设图6中电位器滑动臂旋至离地端1/5处,所以 R\(_{2}\)=10 KΩ/5=2KΩ; R1=R-R\(_{2}\)=8KΩ;Z=ωL=Zπf0L=2KΩ。
最后应注意,安装LC响度补偿电路时,电感线圈应尽量远离电源变压器,或者旋转线圈角度使得交流声最小,或对线圈加屏蔽。(王恭行)