由二极管和电阻组成的与门电路如图1a所示。当它的两个输入端(S\(_{入}\)、EN)均为高电平(3伏)时,二极管D1、D\(_{2}\)均导通,如果忽略二极管的管压降,则输出端(S出)也为高电平;而S\(_{入}\)和EN中只要有一个为低电平(0伏),那么就只有低电平输入的二极管导通,S出则为低电平。如果我们把高电平作为逻辑“1”,低电平作为逻辑“0”,则与门的输出与输入之间的关系可用附表(即与门真值表)来表示。由附表可见,当EN=1时,S\(_{出}\)=S入,也就是脉冲能通过与门;当EN=0时,S\(_{出}\)=0,也就是脉冲不能通过与门。因此EN相当于一个脉冲控制信号。S入、EN和S\(_{出}\)的关系,若用脉冲波形图来表示则如图1b所示。
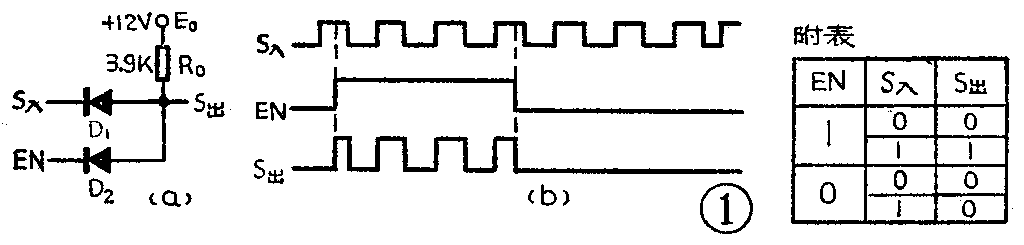
利用与门的特性可以控制脉冲的传送。例如,在测量电动机(或其它转动机械)的转速时,便可利用光电(或其它)转换方式,将电动机的转数变成脉冲数,送到图1a的S\(_{入}\)端,只要精确地控制EN=1的时间,使这个时间正好为1秒,则在所控制的1秒钟内S出端的脉冲个数(用计数设备测出)便为该电动机的转速。
如果我们要测量两台(或多台)电动机的转速,当然可以使用两套(或多套)上述电路和设备。不过,由于计数设备(包括计数器、译码器、显示器等)价格较贵,每一路使用一套很不经济,因此我们便考虑公用一套计数设备,轮流读取两台(或多台)电动机的转速。为了达到这样的目的,我们先试着把两个与门输出端直接连在一起,然后送到共用的计数设备中去(见图2),并分析这样连接能否行得通。显然,如果要测量第一台电动机的转速,则应使S\(_{入1}\)上的脉冲传送到S出上,而S\(_{入2}\)上的脉冲不要传送到S出上。为此,根据图1a的工作原理,应使EN\(_{1}\)=1,EN2=0。但是,当EN\(_{2}\)=0时,D22便优先导通,因而S\(_{出}\)便被箝位在0伏,使输入到S入1端的脉冲无法传送到S\(_{出}\)端上,计数设备也就读不出脉冲数。反之,如果使EN1=0,EN\(_{2}\)=1,S入2同样也传送不到S\(_{出}\)端。由此可见,图2电路是行不通的,而根本原因则是因为两个与门的输出端互相牵制。如果我们能够设法让不传送脉冲的与门输出端(如图2中的S出1或S\(_{出2}\))自动地与总输出端(即图2中的S出)脱离开来,使它不影响S\(_{出}\)端的状态,或者说使它处于“悬浮”状态,问题便可得到解决。为此我们必须把与门电路换成所谓“三态逻辑门电路”。
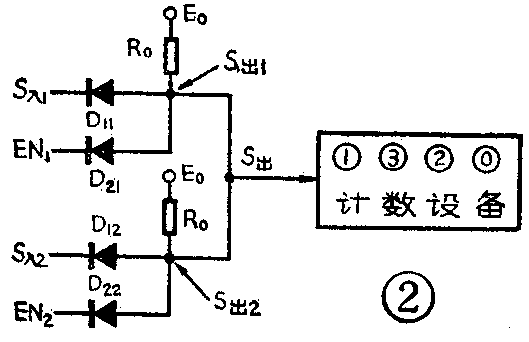
图3a就是一个三态逻辑门电路。其工作原理是,当EN=0时,BG\(_{1}\)截止,BG2饱和,于是BG\(_{3}\)的基极降到约0.2伏,BG3截止,这样便使S\(_{出}\)“悬浮”着,也就是说,由于BG3截止,使S\(_{出}\)与S入和EN断开,S\(_{出}\)不再受S入和EN的影响,这时,其等效电路如图3b所示。当EN=1时,BG\(_{1}\)饱和,BG2截止,因而BG\(_{2}\)便不会对BG3的基极电位产生影响。由于BG\(_{3}\)是一个射极跟随器,因此S入=1时,便有S\(_{出}\)=1;S入=0时,S\(_{出}\)=0,这时电路等效于图3c。
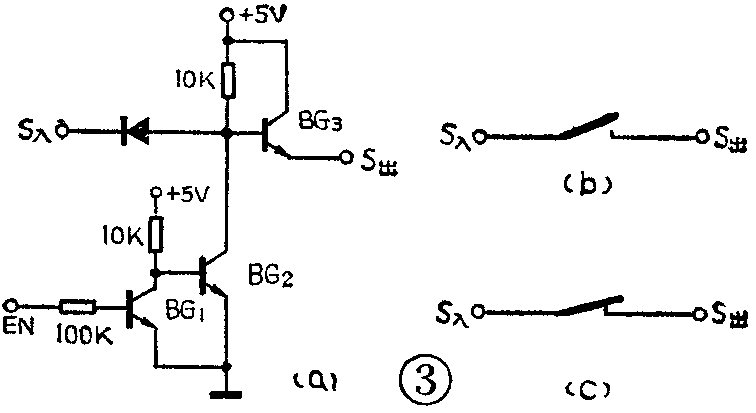
像图3a这样的电路,其输出端除具有0、1状态以外,还有一种“悬浮”状态,因此称为三态逻辑门电路,或称为三态开关。其中具有控制脉冲传输功能的输入信号EN称为“许可”信号。三态逻辑门电路的符号如图4所示。
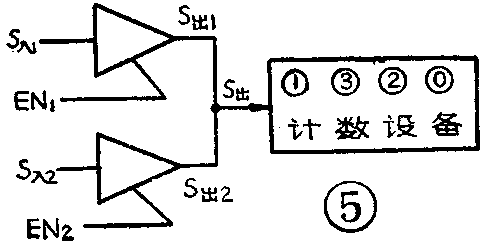
用三态逻辑门电路代替图2中的与门后,便可正确地使S\(_{入1}\)和S入2的脉冲传送至\(_{S出}\)端,见图5。若要传送S入1的脉冲至S\(_{出}\)端,可以使EN2=0,S\(_{出2}\)端便处于悬浮状态,因而对S出没有影响;同时再使EN\(_{1}\)=1,S入1的脉冲便可传送到S\(_{出}\)上。反之,若要传送S入2的脉冲,则使EN\(_{1}\)=0,S出1悬浮;EN\(_{2}\)=1,S入2的脉冲便可传送到S\(_{出}\)上。(杨廷善)