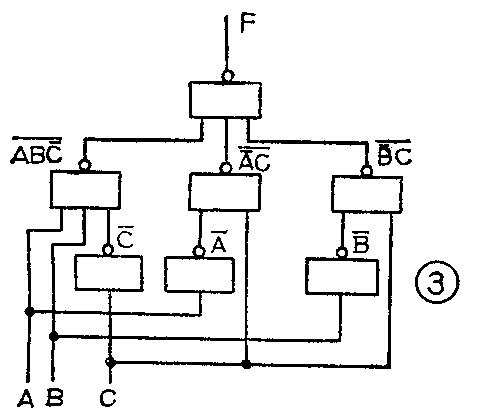
某逻辑电路有三个输入端A、B和C,有一个输出端F。现在只知道它的输入输出的波形为图1,如何用与非门来构成这个逻辑电路?
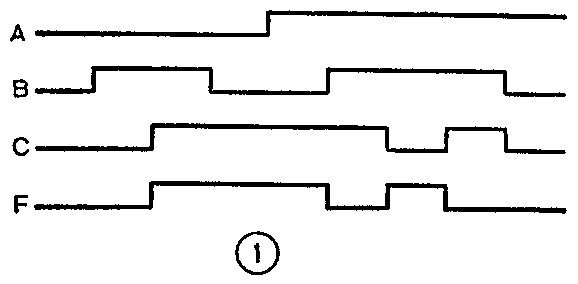
对于这样的问题,必须首先分析波形图,找出输入A、B、C为各种状态组合时输出F所对应的状态。为此,在图1的波形上,把凡是A、B、C的波形状态有改变的地方,都画上垂直的虚线,并直达于输出F的波形上,见图2。然后在各条垂直虚线所划分的间隔内,将A、B、C和F的状态都用1或0标注出来(低电平为0,高电平为1)。于是便可将上述每一间隔内的情况列成表格(见附表)。显然,附表便是这个未知逻辑电路的真值表。
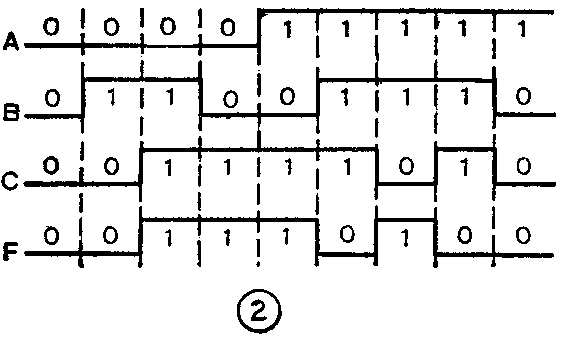

其次,根据真值表求逻辑表达式。方法是把F=1的各项相加,于是得
F=A-B-C+AB-C-C+ABC-
将上式用逻辑代数的基本公式进行化简:
F=A-B-C+A-BC-C+ABC-
=A-C(B-+B)-C+ABC-
=A-C+ABC-+ABC-(∵B-+B=1)
=C(A--)+ABC-
=C(A--B--)+ABC-(∵A--B-)
=C[A---+A)]+ABC-
=C(A--)+ABC-(∵A-+A=1)
-C+B-C+ABC-
=A-C+B-C+ABC-
=A-C·B-C·ABC-(摩根定理)
F=A-C+B-C+ABC-
F=(A--)C+ABC-
=AB-C +ABC---=AB-摩根定理)
=AB-C·ABC-(摩根定理)
由此式可得图4所示的逻辑电路。显然,图4比图3更简单一些。
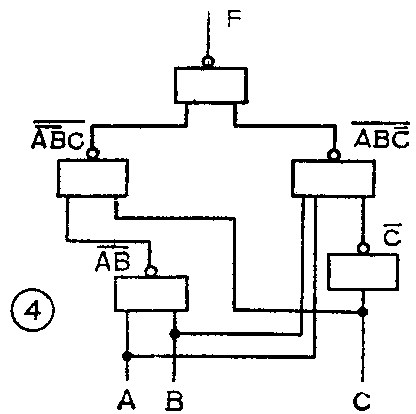
这个例题给了我们一个启发:设计逻辑电路的时候,最好多试探几种方案,以便找出最佳的方案。而且基本公式掌握得越熟练,最佳方案越容易找到。(杨廷善)