中频变压器为什么要抽头

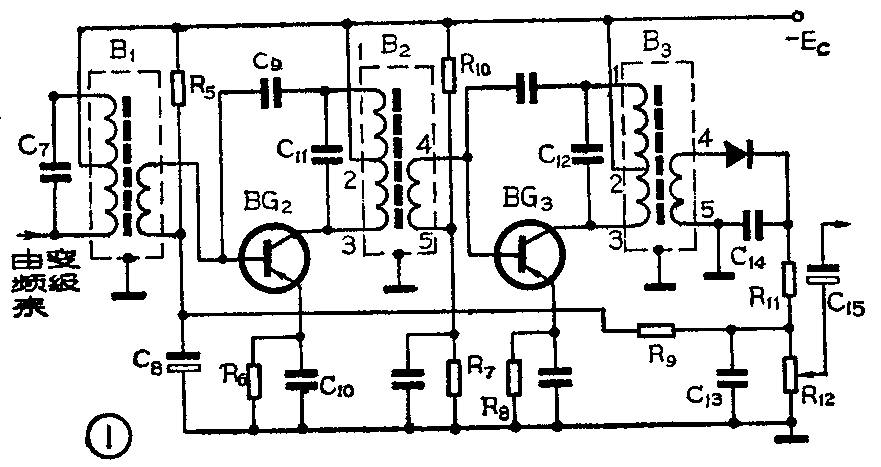
图1是晶体管超外差式收音机中频放大器的整体线路，其中B\(_{1}\)2\(_{3}\)是中频变压器（即中周）。它们的初级线圈分别与电容 C7、C\(_{11}\)、C12组成中频调谐回路。从图1我们发现这样一个问题，就是变频管和中放管的输出不是接到调谐回路电感线圈的两端，而是接到电感线圈的抽头上，也就是将电感部分接入。为什么要采用这种接法呢？这就是本文所要说明的问题。

为了说明为什么要采用电感部分接入，必须分析采用电感全部接入时会出现什么问题。我们以图1中的第一中放BG\(_{2}\)为例，并假定它的调谐回路采用电感全部接入电路，即把BG2的输出端跨接到电感线圈两端AB上（见图2）加以分析。

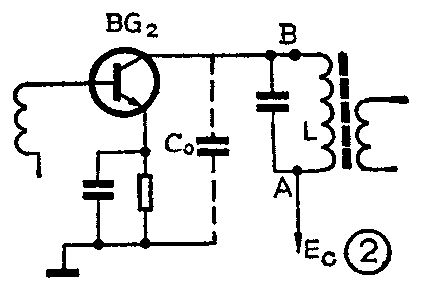
首先讨论功率或者说能量的传输问题。由图2可见，这个由L和C组成的中频调谐回路是并联谐振回路。如果我们把中放管BG\(_{2}\)看成是信号源，那么该谐振回路就是它的负载。我们知道，负载上获得最大功率的条件是负载电阻等于信号源内阻，即通常所说的阻抗匹配。在我们所讨论的问题里，负载阻抗是LC并联谐振回路的谐振阻抗，信号源内阻就是晶体管BG2的输出阻抗。为了达到阻抗匹配，就要求这两个阻抗相等。晶体管BG\(_{2}\)的输出阻抗虽然由于集电结反向偏置，因而比输入阻抗高，但一般也只有十几千欧左右，而并联谐振回路的谐振阻抗则比它高很多，约在几十千欧，两者差别大，不匹配，因此全部接入电路不能满足最大功率传输的要求。

第二，采用全部接入电路时，BG\(_{2}\)的输出阻抗对谐振回路Q值的影响较大。对于超外差式收音机的中频调谐回路，从选择性角度看，希望Q值高一些，因为Q值越高，选择性越好。但从通频带角度看，Q值高，则通频带变窄，因此又要求Q值不能太高。为了兼顾通频带及选择性两方面的要求，一般把Q值选到某个中间数值，并希望它不变。但是，全部接入电路是把BG2的输出阻抗直接并联到谐振回路的两端，而且这个输出阻抗又较小，这就增加了回路的损耗，从而使Q值降低，这样就降低了收音机的选择性。

第三，由于晶体管BG\(_{2}\)直接跨在调谐回路的两端，因此它的输出电容（即图2中的C0）就与谐振回路并联，这就相当于在谐振回路的电容上又并了一个C\(_{0}\)（在频率较高时，它的影响就不能忽略），使总的回路电容发生变化，因而谐振频率就发生了变化，使中放的工作频带发生移动。

由于全部接入电路存在着以上三个问题，因此一般都采用部分接入电路。下面我们分析部分接入电路是怎样解决这三个问题的。

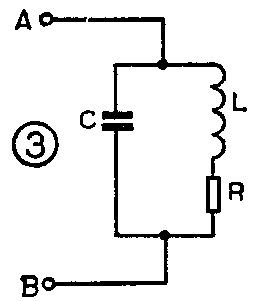
我们将图2中的并联谐振回路单独画出来如图3所示。其中电阻R为谐振回路的损耗电阻（主要是电感的损耗）。我们知道，从AB两点之间看进去的阻抗是L和C两条支路的阻抗并联值，由于谐振时，电感支路的感抗ω\(_{0}\)L与电容支路的容抗\(\frac{1}{ω}\)0C相等，因而它们之和等于0，即ω\(_{0}\)L-1;ω0C=0，这时AB之间的阻抗最大，并且是纯电阻，其数值为：

R\(_{0}\)e就叫作回路的谐振阻抗。

式中ω\(_{0}\)为谐振频率，由于谐振时ω0L=\(\frac{1}{ω}\)\(_{0}\)C可知ω0=1;\(\sqrt{Lc}\)。所以又有R\(_{0}\)e=\(\frac{L}{CR}\)。

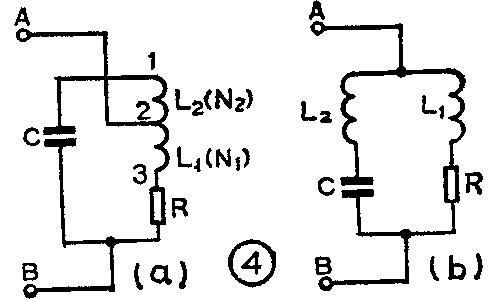
采用部分接入电路时，BG\(_{2}\)的输出被接到电感L的2、3两抽头之间（见图1），这时谐振回路可用图4a表示。显然图4a又可以变换成图4b（只是画法改变，电路结构没变），这就可以清楚地看出，采用部分接入法，BG2的输出端连接的是图4b所示的并联谐振回路。把它与图3进行比较可知，图4b的总电感L\(_{1}\)＋L2就等于图3中的L，因此图4b回路的谐振频率没有因为改变接法而发生变化，仍为ω\(_{0}\)=1\(\sqrt{LC}\)。但是，图4b的一条支路为电感L1，另一条支路为电感L2和电容C，好象变成了一个复杂的谐振回路，然而只要电容C和电感L\(_{2}\)的数值选得适当，完全可以使L2的感抗小于C的容抗而最终使这一支路呈容性电抗，结果就变成了与图3的形式相同的简单并联谐振回路，只是这时电感支路的电感由L变成了L\(_{1}\)。于是，在求AB两点间的谐振阻抗时，ω0L变成了ω\(_{0}\)L1，所以图4b的谐振阻抗就变成了

如果我们把部分接入的电感量L\(_{1}\)与总电感量L之比叫作接入系数，并以PL表示，则P\(_{L}\)=L1L\(_{1}\)+L2=L\(_{1}\);L，于是就得到了L1=P\(_{L}\)L。将L1代入R\(_{0}\)e′式中则得

可见部分接入与全部接入时的谐振阻抗相差PL\(^{2}\)倍。由于PL小于1，因此R\(_{0}\)e′小于R0e。显然，只要选择适当的接入系数PL，就可以使谐振阻抗的数值按我们的要求变化，作到与BG\(_{2}\)的输出阻抗匹配，以满足最大功率传输的条件。

什么是谐振回路的Q值呢？我们知道，LC振荡回路在谐振时，回路中储存的能量最大，这种能量是以电感线圈中磁场能的形式和电容器里电场能的形式交替变化着，磁场能最大时，电场能为0，反之也一样。如果以磁场能来表示回路储能的总值，则有W\(_{总}\)=1;2LI\(^{2}\)m。I\(_{m}\)是振荡电流的振幅值。另一方面，回路在谐振时，又总是对振荡电流产生一定的损耗。在一个振荡周期内，损耗的能量为 W损＝I2\(_{m}\)RT。R为回路的损耗电阻，T为振荡同期。不同的振荡回路，损耗电阻大小不同。我们可以把上述的W总与W\(_{损}\)进行比较，来衡量这个谐振回路品质的好坏，则

由于T=1/f\(_{0}\)。ω0=2πf\(_{0}\)，所以T=2π/ω0。将T代入上式则有

Q就叫作回路的品质因数。很明显，它的物理意义就是谐振回路在谐振时，回路中储存的能量与一周期内损耗能量之比的2π倍。因为

其中L是回路的总电感，C是总电容，R是总的损耗电阻。由此可见，只要回路中这三个量不变，Q值就不会变。

明确了Q值的物理意义及影响它变化的因素以后，我们再分析BG\(_{2}\)的输出阻抗是怎样影响谐振回路Q值的。

先考虑全部接入时的情况：我们把图3中的损耗电阻R等效成与LC并联的R\(_{0}\)，见图5a，这时的LC谐振回路就是没有损耗的理想谐振回路，它的谐振阻抗为无穷大，因此在谐振时，从图5a的AB两点看进去的阻抗就是电阻R0。又因图5a与图3等效，所以图5a中的R\(_{0}\)在数值上就等于图3中的谐振阻抗R0e，即

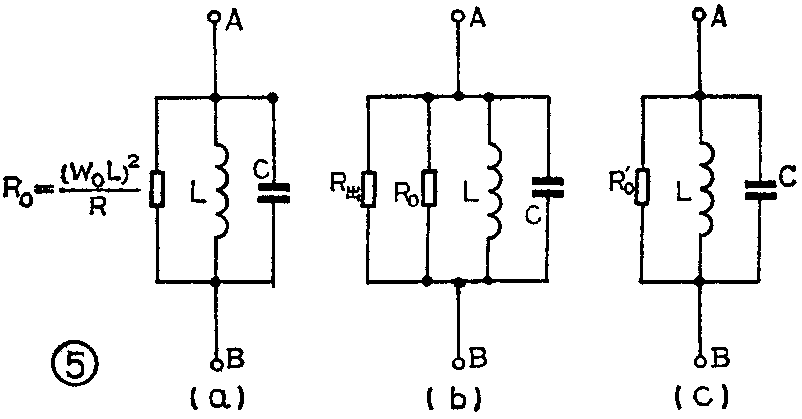
由此得出Q=R\(_{0}\)ω0L。显然，谐振回路的Q值与R\(_{0}\)成正比，R0越大，Q值就越大，R\(_{0}\)减小，则Q值也减小。由于全部接入电路就是把BG2的输出阻抗R出直接跨接到LC并联谐振回路的两端（见图5b、c），这时R\(_{0}\)与R出并联，而R\(_{出}\)又比R0小，所以总电阻R\(_{0}\)′减小，谐振回路的Q值就减小。那么采用部分接入电路为什么能使R出对Q值的影响减小呢？因为在部分接入时，BG\(_{2}\)的输出阻抗是并接到电感线圈L的一部分上，如图6所示。要考虑它对Q值的影响，可以把R出折算成接到L两端的等效电阻R\(_{折}\)，再讨论R折的大小。大家知道，有抽头的电感线圈实际就是一个自耦变压器，而变压器的阻抗比等于圈数的平方比。设BG\(_{2}\)的输出阻抗R出接到L\(_{1}\)的圈数为N1，线圈L的总圈数为N\(_{1}\)＋N2，则R\(_{出}\)与R折的关系为：

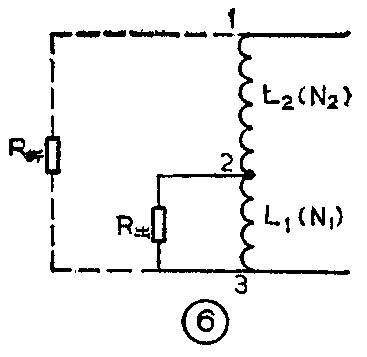
n是一个大于1的数字，所以R\(_{折}\)要大于R出。这就是说，BG\(_{2}\)的输出阻抗虽然较小，但是由于是接到电感线圈的一部分上，当把它折算到与整个线圈并联时，其等效电阻的数值就被大大提高了。因而相当于在L两端并上了一个大电阻。例如中源变压器TTF－2－2，它的N1是45匝，N1+N\(_{2}\)是162匝，n=3.6，n\(^{2}\)≈13，R折≈13·R\(_{出}\)。即接到电感线圈两端的等效电阻比BG2的输出阻抗大13倍，因而对R\(_{0}\)的影响，也就是对Q值的影响大大减小了。

我们知道，谐振回路的谐振频率。ω\(_{0}\)只决定回路的总电感L和总电容C，采用部分接入电路只改变了BG2的发射极与线圈连接的位置，并没有改变总电感L的数值，因此，如果不考虑BG\(_{2}\)输出电容C0的影响，则不论是全部接入电路，还是部分接入电路，其谐振频率应当没有变化。但是，前面提到在采用全部接入电路（见图 2）时，电容C\(_{0}\)是直接并联到回路电容C上的，因而对谐振频率会产生一定影响。而采用部分接入电路以后，电容C0是并接到线圈L\(_{1}\)上的（见图7），其容抗值为\(\frac{1}{ω}\)0C\(_{0}\)，这时要考虑C0对谐振频率的影响，也要把C\(_{0}\)折算到线圈L的两端，变成C0′，其容抗值为1;ω0\(_{C}\)0′。同样根据自耦变压器阻抗变换原理，这两个容抗之比，等于它们各自接入的圈数平方比，即

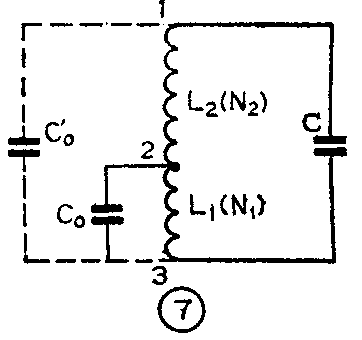
由此可见，折算后与回路电容C并联的等效电容C\(_{0}\)′比C0减小了\(\frac{1}{n}\)\(^{2}\)倍。因而对C的影响，也就是对谐振频率的影响大为减小，可以不考虑了。

至此，前面提到的三个问题都得到了解决，这就是中频变压器所以要采用部分接入电路（即抽头）的原因。(周维田)