以前曾介绍过RC衰减型音调控制电路,本文再介绍一种反馈型音调控制电路。这两种电路从性能上说各具特点,可以满足不同类型听音者的需要,因此常被业余爱好者采用。
“反馈型”电路的特点?
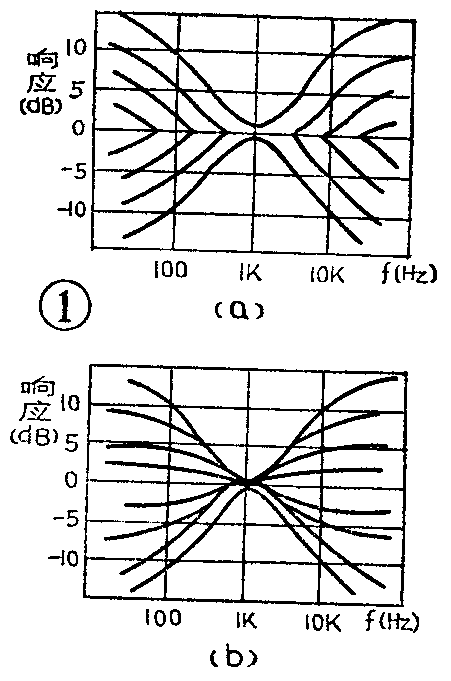
让我们还是用控制特性曲线来说明。反馈型音调控制电路的控制特性见图1a,RC型衰减式控制电路的控制特性见图1b,可以明显地看出,前者的转折频率点随着音调的调节而发生移动,但其控制特性曲线的斜率确保持每倍频程衰减6分贝,并不受音调调节的影响;后者的控制特性与前者正好相反,在调节音调时,其转折频率固定不变,但特性曲线的斜率却随之改变。
“反馈型”电路是怎样构成的?
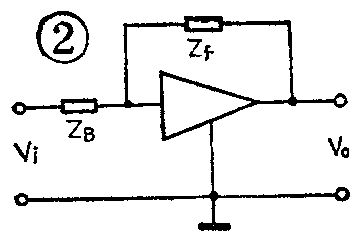
图2为这种电路的方框图,它是一个电压并联型负反馈电路。图中的放大单元可由晶体管、场效应管、电子管或线性集成电路组成。如果用Z\(_{f}\)代表反馈回路的总阻抗,用ZB代表输入回路的总阻抗,则反馈系数为B=Z\(_{B}\)/Zf。当放大器的开环放大倍数K.\(_{v}\)很高,且满足K.V·B》1时,电压并联负反馈电路的闭环增益为K.\(_{vf}\)=Vo/V\(_{i}\)=1/B=Zf/Z\(_{B}\)。
为了分析简便起见,我们来看一看图3几个特殊情况;图3a(图中四个电路的标号由上至下分别为a、b、c、d)为反馈型低音提升电路。反馈回路的总阻抗Z\(_{f}\)由R2和C\(_{2}\)串联而成,即Zf=R\(_{2}\)+1/jωC2。输入回路的总阻抗Z\(_{B}\)就是R1,所以
K·\(_{vf}\)=R2R\(_{1}\)(1+1;1+jωC2·R\(_{2}\))。
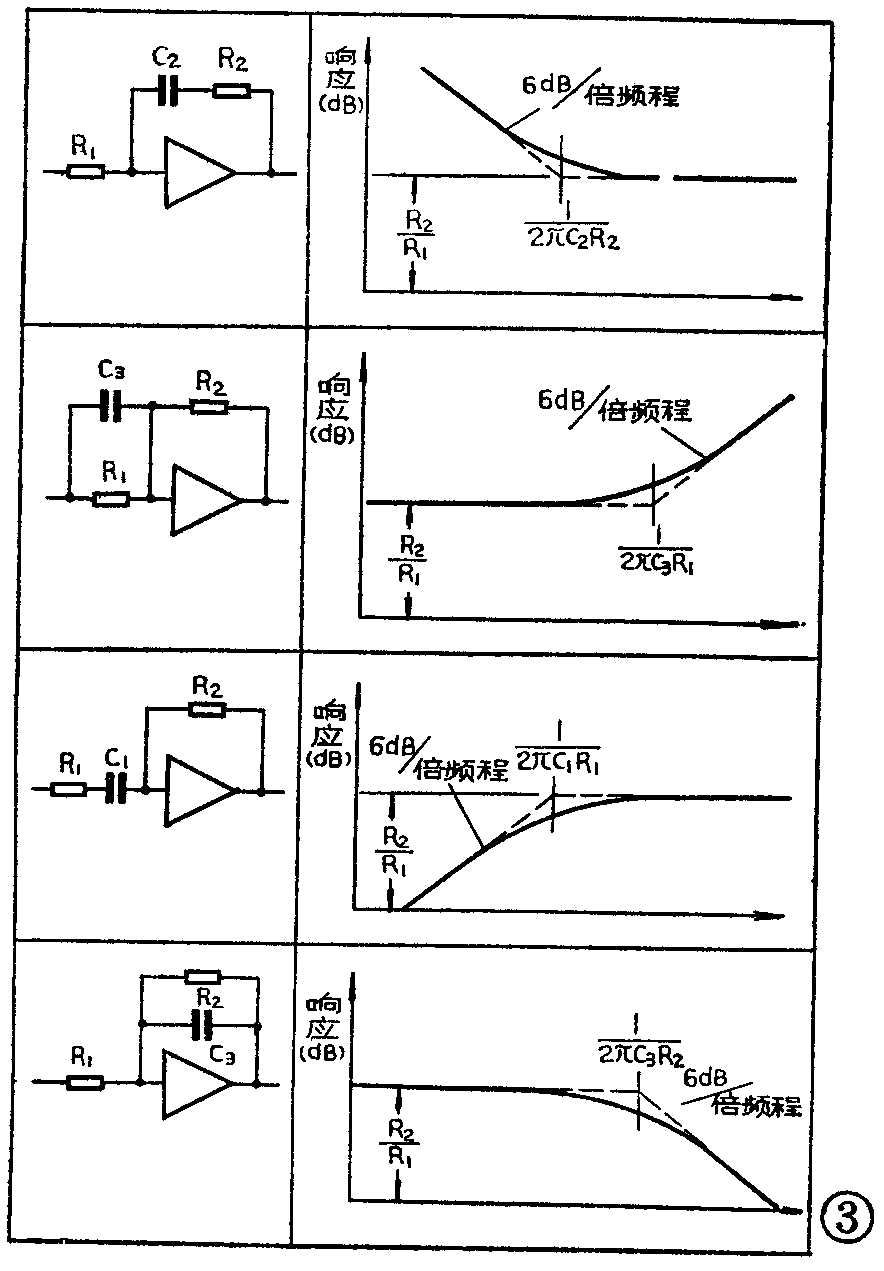
频率高于中音时,C\(_{2}\)可认为短路(即\(\frac{1}{jωC}\)2=0),Z\(_{f}\)=R2,则K·\(_{vf}\)=R2/R\(_{1}\),K·vf与频率无关;当频率低于中音时,C\(_{2}\)的容抗增大,Zf增大,K\(_{vf}\)也随频率的降低而增高。频率每降低一倍,增益则增加一倍,形成每倍频程按6分贝增大的低音提升曲线。
图3b为高音提升电路。输入回路的总阻抗Z\(_{B}\)是由R1与C\(_{3}\)并联而成的,即ZB=R\(_{1}\)/(1+jωC3R\(_{1}\))。反馈回路的阻抗Zf=R\(_{2}\)。则电压闭环增益为K·vf=Z\(_{f}\)/ZB=\(\frac{R}{_{2}}\)R1(1+jωC\(_{3}\)R1)。在中、低音时,C\(_{3}\)近似开路,此时K·vf为一恒定值,即K·\(_{vf}\)=R2/R\(_{1}\);频率一旦高于中音,C3不能认为短路,C\(_{3}\)的容抗随频率升高而减小,于是引起ZB减小,K·\(_{vf}\)增大。
图3c为低音衰减电路。图中C\(_{1}\)串联于输入回路中,不难推导出
K·\(_{vf}\)=R2R\(_{1}\)·1;1+\(\frac{1}{jωC}\)1R\(_{1}\)
由于C\(_{1}\)对中音和高音容抗很小,再认为短路,即可认为1/jωC1R\(_{1}\)《1,则K·vf≈R\(_{2}\)/R1,是一个常数;当频率低于中音时,C\(_{1}\)的容抗随频率降低而增大,ZB增大,K·\(_{vf}\)随之降低,所以图3c起低音衰减作用。
图3d起高音衰减作用。K·\(_{vf}\)=R2R\(_{1}\)1;1+jωC3·R\(_{3}\)。在中音和低音时,C3近似开路,K·\(_{vf}\)=R2;R\(_{1}\),与频率无关;频率高于中音时,C3容抗随频率升高而降低,K·\(_{vf}\)随之下跌。
在实用电路中,需要将上述四个独立电路综合成一个网络,而且要求通过调节某些元件,能把上述各个电路的特性独立显现出来。图4就是按照这种要求而设计的。
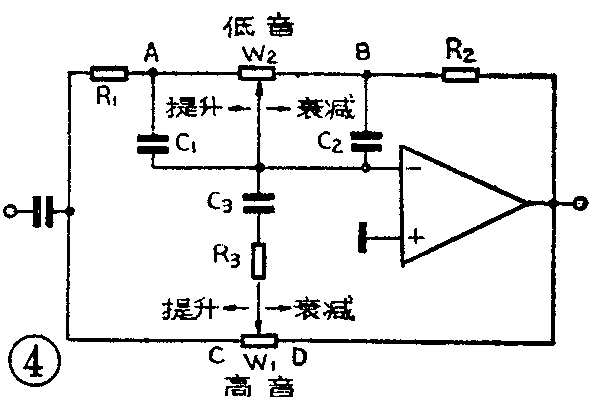
具体电路分析
图4中,对于中、低音频信号来说,由于C\(_{3}\)容量较小,可视为开路。W1阻值也较大,可视为开路,于是图4简化为图5a。当电位器W\(_{2}\)的滑臂移到A点时,C1被短路,于是构成如图5b所示的低音提升电路。可以看出,它与图3a的区别,仅在于在C\(_{2}\)两端多并联了一个W2。此时反馈网络的总阻抗为
Z\(_{f}\)=R2+\(\frac{W}{_{2}}\)1+jωC2W\(_{2}\),
幅频特性变为K\(_{vf}\)=R2+W\(_{2}\)R1\(\sqrt{1}\)+(\(\frac{ω}{ω}\)\(_{L2}\))\(^{2}\)1+(ω;ωL1)2。
式中,ω\(_{L1}\)=2πfL1=\(\frac{1}{C}\)\(_{2}\)W2,ω\(_{L2}\)=2πfL2=W\(_{2}\)+R2;C\(_{2}\)·W2·R\(_{2}\),
ω\(_{L1}\)是曲线由提升转入平滑时的转折角频率,ωL2为特性曲线开始提升时的转折角频率。W\(_{2}\)的引入不仅是起音调调节作用,而且它对转折角频率也有影响,所以W2的阻值不能随便选取。
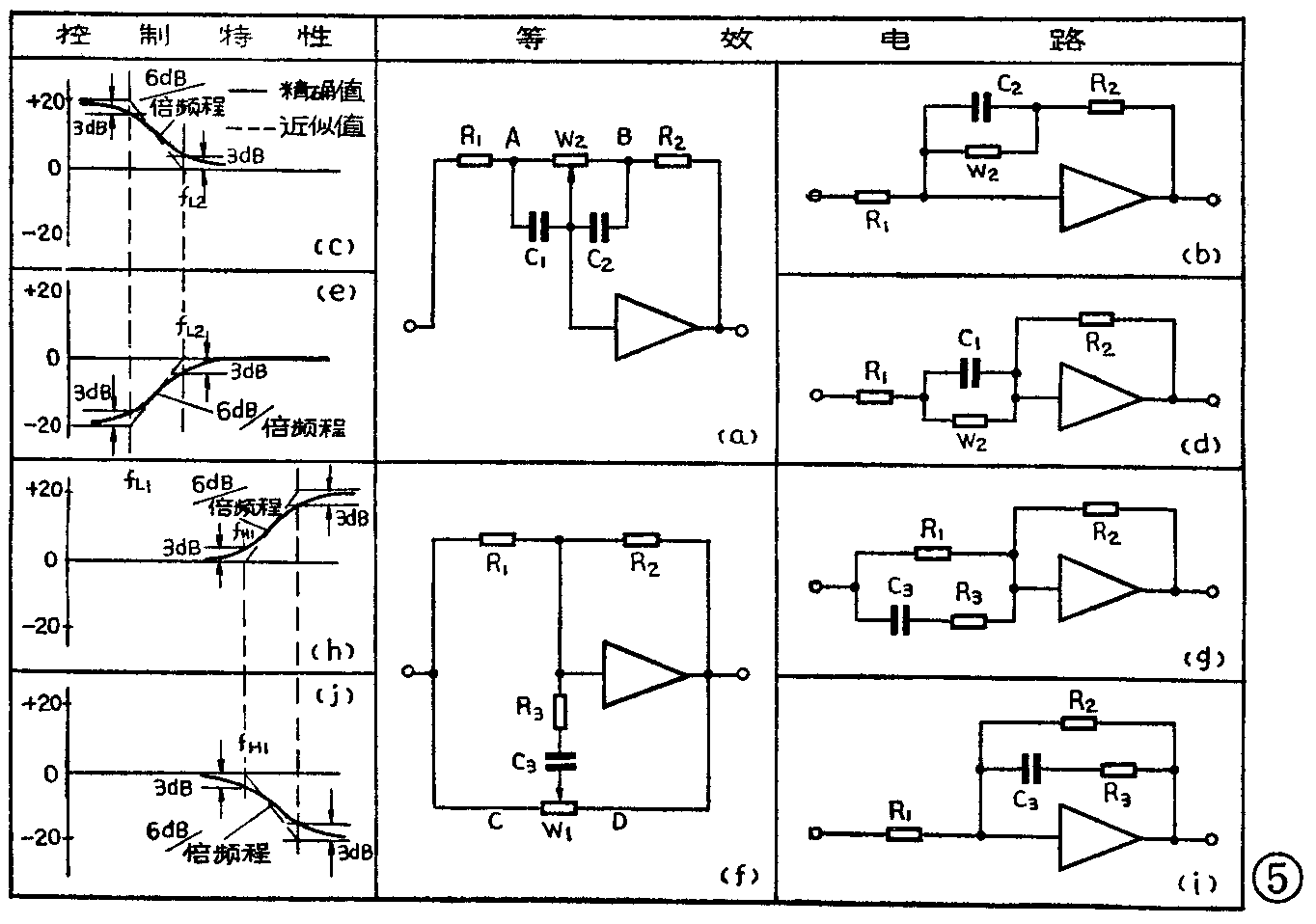
下面通过一个具体例子进行定量分析:以图5a低音提升电路为例,通常选R\(_{1}\)=R2,W\(_{2}\)=9R2,则根据前面计算ω\(_{L1}\)、ωL2的公式,很快可以得出ω\(_{L2}\)=10ωL1,也可写成f\(_{L2}\)=10fL1。当频率处于中、高音频时,因为(\(\frac{ω}{ω}\)\(_{L2}\))\(^{2}\)》1,则必然也满足(ω;ωL1)2》1,则幅频特性K\(_{vf}\)≈R2+W\(_{2}\)R1·ω\(_{L1}\);ωL2=10×110=1,此时的增益为1,用分贝表示就是零分贝,其特性是一条平坦的直线。定性来说,就是在中、高音域,增益仅取决于R\(_{2}\)与R1的比值,即K\(_{vf}\)=R2/R\(_{2}\)=1。
当频率极低时,即f趋近于零时,ω《ω\(_{L1}\),故有(ω/ωL1)\(^{2}\)《1,(ω/ω\(_{L2}\))2《1,此时Kvf≈\(\frac{R}{_{2}}\)+W2R\(_{1}\)=10,即增益为20分贝。这也就是说,当信号频率很低时,C2可视为开路,其增益仅决定于R\(_{2}\)和W2串联后再与R\(_{1}\)之比。
当信号的角频率ω=ω\(_{L2}\)时,
K\(_{vf}\)=R2+W\(_{2}\)R1·\(\sqrt{1}\)+(\(\frac{ω}{_{L2}}\)ωL2)\(^{2}\)1+(ω\(_{L2}\);ωL1)2=10·\(\frac{1+1}{1+10}\)\(^{2}\)≈1.4,
也就是K\(_{vf}\)为3分贝;当信号角频率ω=ωL1时,可以求出K\(_{vf}\)=7.07,即+17分贝。图5c为用对数形式表示的低音提升幅频特性,可以看出,在转折频率fL2处提升了3分贝;在转折频率f\(_{L1}\)处,其提升量比最大提升量(20分贝)低3分贝。
当图5a中W\(_{2}\)的滑臂置于B点时,C2被短路,电路等效成图5d,这是一个低音衰减电路。与图3c相比,仅是在C\(_{2}\)两端多并联了一个W2。此时的幅频特性可写为
K\(_{vf}\)=R2R\(_{1}\)+W2·\(\sqrt{1}\)+(\(\frac{ω}{ω}\)\(_{L1}\))\(^{2}\)1+(ω;ωL2)2
式中,ω\(_{L1}\)=2πfL1=1/C\(_{1}\)·W2,ω\(_{L2}\)=2πfL2=(W\(_{2}\)+R1)/C\(_{1}\)·W2·R\(_{1}\)。
在频率处于中、高音时,可视为(\(\frac{ω}{ω}\)\(_{L2}\))\(^{2}\)》1,(ω;ωL2)2》1,则K\(_{vf}\)≈R2R\(_{2}\)+W2·ω\(_{L2}\);ωL1=110×10=1,即等于零分贝;当频率很低时,K\(_{vf}\)≈R2;R\(_{1}\)+W2=\(\frac{1}{10}\),即等于-20分贝;当频率ω=ω\(_{L2}\)时,Kvf为-3分贝;当ω=ω\(_{L1}\)时,Kvf为-17分贝。其低音衰减控制特性如5e。
分析高音电路时,可将图4中的C\(_{1}\)、C2短路,于是变成图5f形式。将电位器滑臂滑到C点,便构成图5g高音提升电路。将滑臂移到D点,则形成图5i高音衰减电路。与图3b和图3d对照,图5g和图5i中的C\(_{3}\)支路都多加了一个R3。R\(_{3}\)起限制高音最大控制量的作用。高音提升时的转折角频率,ωH1=1/C\(_{3}\)(R1+R\(_{3}\)),高音衰减时的转折角频率ωH1=1/C\(_{3}\)·(R2+R\(_{3}\)),高音提升和高音衰减电路中,限制最大控制量的转折角频率均为ωH2=1/C\(_{3}\)·R3。高音提升和高音衰减电路的控制特性分别见图5h和图5j。
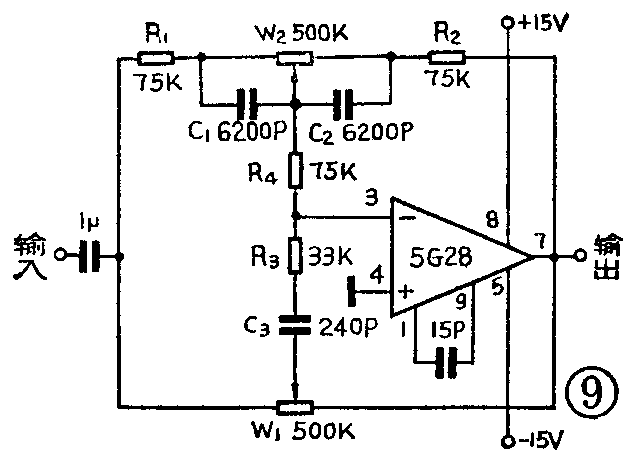
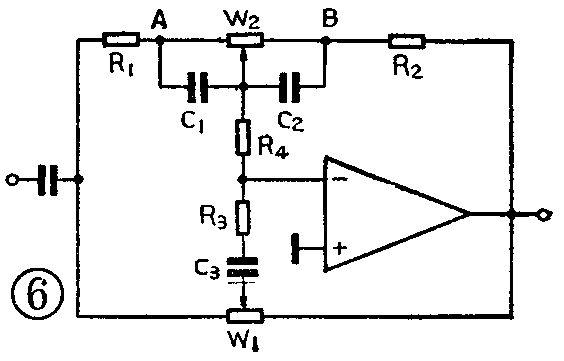
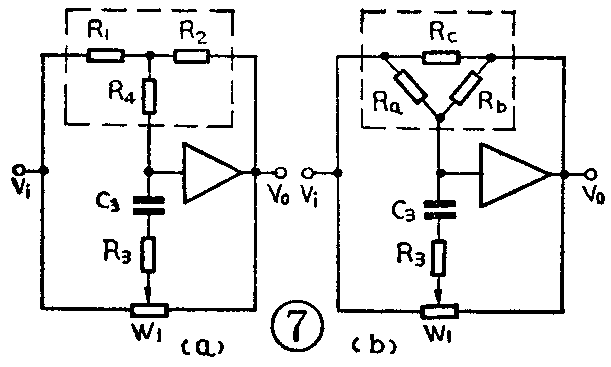
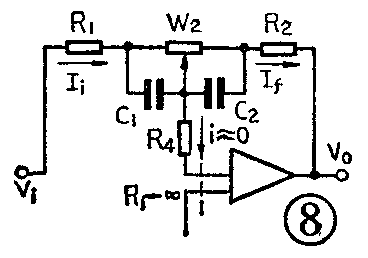
在实用电路中,常如图6所示再增加一个电阻R\(_{4}\)。附加R4的好处是使选择高音转折频率更自由一些,对低音调整电路影响不大。例如,对于高音电路来说,图6可以简化成图7a。为了分析方便,图7b中将R\(_{1}\)、R2、R\(_{4}\)换成三角形连接形式。其中Ra=R\(_{1}\)+R4+\(\frac{R}{_{1}}\)·R4R\(_{2}\),Rb=R\(_{2}\)+R4+R\(_{2}\)·R4;R\(_{1}\),Rc=R\(_{1}\)+R2+\(\frac{R}{_{1}}\)·R2R\(_{4}\)。通常取R1=R\(_{2}\),则Ra=R\(_{b}\)=R1+2R\(_{4}\)。如果令R1=R\(_{2}\)=R4,则R\(_{a}\)=Rb=3R\(_{1}\)。如果前级采用内阻极小的电压源激励,那么通过Rc支路的反馈电流将为信号源的低内阻所旁路,R\(_{c}\)的反馈作用则可忽略不计(可视为开路),其电路形式与图5f就一样了,只是转折频率有变化。此时fH1=1/2πC\(_{3}\)(Ra+R\(_{3}\))或fH1=1/2πC\(_{3}\)(Rb+R\(_{3}\));对于低音电路来说,图6可简化为图8。可以看出,虽然在放大器输入端加了一个电阻R4,但因放大器件的输入阻抗很高,开环放大倍数非常大,所以输入回路的电流i\(_{i}\)将全部流经反馈回路,即ii=i\(_{f}\),流进器件的电流几乎为零。所以R4对低音调整电路的反馈作用可以忽略。注意:上述假设条件以放大器件的放大倍数极高及器件的输入阻抗极高为前提。集成运算放大器容易满足这种条件。如果采用晶体管放大器,应尽量选用高β的管子。
设计举例 设计要求:
要求设计一个反馈型音调控制电路,其控制特性为:低音在100赫时±12分贝,高音在10千赫时为±12分贝,并规定低音和高音控制频率点分别限制在50赫和20千赫。
设计步骤:1.确定放大单元的器件:选用5G28集成电路运算放大器。由于5G28集成运放块在内部电路中以结型场效应管作输入级,具有输入阻抗高的特点,可达到10\(^{9}\)欧,故能很好地满足控制特性的要求,只需要采用小容量电容器即可。
2.计算转折频率点f\(_{L2}\)、fH1:利用控制特性的斜率为每倍程6分贝的规律,及在100赫和10千赫处有±12分贝提升量的要求,可算得低频转折频率f\(_{L2}\)为100赫的二个倍频程,即fL2=100赫×2\(\frac{^{12}}{6}\)=100×4=400赫。也可以算得高频转折频率点
f\(_{H1}\)=\(\frac{10千赫}{2}\)\(^{12;6}\)=2500赫。
3.选择控制电位器:考虑到5G28运放块输入阻抗很高,所以W\(_{1}\)W2的阻值可适当选高一些,可选W\(_{1}\)=W2=500千欧。选用“Z”形电位器较好。
4.计算低音调整电容C\(_{1}\)、C2:由C\(_{1}\)·W2=C\(_{2}\)W2=\(\frac{1}{2πf}\)\(_{L1}\)的关系,得C1=C\(_{2}\)=1;2πfL1W\(_{2}\)=\(\frac{1}{6.28×50×500×10}\)\(^{3}\)≈6.4×10-9法=6400微微法。 选取C1=C\(_{2}\)=6200微微法。
5.电阻R\(_{1}\)、R2的确定和计算:
由f\(_{L1}\)=\(\frac{1}{2πC}\)2W\(_{2}\)及fL2=W\(_{2}\)+R2;2πC\(_{2}\)W2R\(_{2}\)的关系,得R2=\(\frac{W}{_{2}}\)(fL2;f\(_{L1}\)-1)=\(\frac{500×10}{^{3}}\)400;50-1=71.4千欧;同理,由式fL1=\(\frac{1}{2πC}\)\(_{1}\)W2及f\(_{L2}\)=W2+R\(_{1}\);2πC2W\(_{2}\)R1的关系,可求出R\(_{1}\)=71.4千欧。取R1=R\(_{2}\)=75千赫即可。
6.确定电阻R\(_{4}\)及R3:如果取R\(_{4}\)=R1=R\(_{2}\)=75千欧,则Ra=3R\(_{1}\)=225千欧。由fH1=\(\frac{1}{2πC}\)\(_{3}\)(R3+R\(_{a}\))和fH2=1;2πC\(_{3}\)·R3的关系,得R\(_{3}\)=Raf\(_{H2}\);fH1-1=225千欧20×10\(^{3}\);2.5×103-1≈32千欧。取R\(_{3}\)=33千欧。
7.计算高音调整电容C\(_{3}\):
由f\(_{H2}\)=\(\frac{1}{2πC}\)3·R\(_{3}\)得C3=1;2πf\(_{H2}\)·R3=\(\frac{1}{6.28×20×10}\)\(^{3}\)×33×103=2.4×10\(^{-}\)10法=240微微法。取标称值C\(_{3}\)=240微法。(郭维芹)