在计算输出变压器的变比n时,读者可能发现一些书刊上的计算公式不一致。例如,有的写
n=\(\frac{\sqrt{ηB·R}}{_{1}}\)R2,有的写n=R\(_{1}\);ηB·R2。
式中ηB为变压器的效率,R\(_{1}\)为从变压器初级看进去的等效阻抗, R2为次级的等效阻抗,当输出端接上负载R\(_{L}\)时,R2=R\(_{L}\)。为什么会出现这种情况呢?在具体设计变压器时,如何考虑ηB的位置呢?下面就详细讲讲这个问题。
先从理想变压器谈起
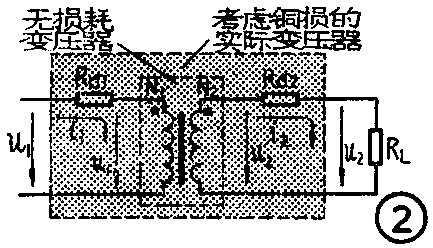
一个理想变压器,本身不损耗任何功率,或者说,初级所吸收的功率全部输送给了负载。这时,如图1所示,P\(_{1}\)=P2=P\(_{L}\),P1=u\(_{1}\)·i1,P\(_{2}\)=u2·i\(_{2}\)。式中P1、u\(_{1}\)、i1分别为初级的功率、电压、电流,P\(_{2}\)、u2、i\(_{2}\)分别为变压器次级的功率、电压、电流,PL为次级负载上所获得的功率。
根据变压器的变压原理,图1变压器的变压比为n=u\(_{1}\)/u2=N\(_{1}\)/N2。式中N\(_{1}\)、N2为变压器初、次级绕组的匝数。则i\(_{1}\)/i2=1/n。上面式子说明:初、次级的电压比与变比n成正比,初、次级的电流比与变比n成反比。
利用变压器能够实现电压变换和电流变换这一特点,可以实现阻抗变换。在变压器次级接有负载R\(_{L}\)时,RL=R\(_{2}\)=u2/i\(_{2}\)。同理R1=u\(_{1}\)/i1。则初、次级阻抗之比为
R\(_{1}\)/R2=U\(_{1}\)/i1·i\(_{2}\)/u2=u\(_{1}\)/u2·i\(_{2}\)/i1=n\(_{2}\),或n=
有损耗时的计算方法
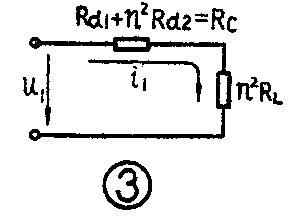
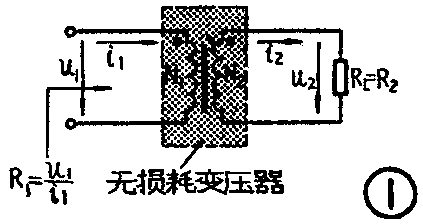
1.铜损。铜损是由绕组的导线电阻(直流电阻)引起的。如果撇开其它损耗,只由绕组的导线电阻造成的损耗可用图2等效电路表示。图中初、次级绕组的直流电阻分别用R\(_{d1}\)、Rd2表示,它的特点是R\(_{d1}\)和初级线圈串联,Rd2和次级线圈串联。因为有了R\(_{d1}\),在Rd1上则要产生电压降,所以在变压器的输入功率P\(_{1}\)=u1i\(_{1}\)中,需扣除在Rd1上消耗的功率,而只有u\(_{1}\)′·i1输送给次级,即u\(_{1}\)′·i1=u\(_{2}\)′·i2。变比为n=u\(_{1}\)′/u2′=i\(_{2}\)/i1,或n\(^{2}\)=\(\frac{u}{_{1}}\)′i1/u′\(_{2}\);i2。次级的R\(_{d2}\)也要白白消耗一部分功率,它和负载电阻RL串联后反射到初级去的阻抗为u1′i\(_{1}\)=n2u2′;i\(_{2}\)=n\(^{2}\)(RL+R\(_{d2}\)),式中n2Rd2为R\(_{d2}\)的反射阻抗,n\(^{2}\)RL为R\(_{L}\)的反射阻抗。 Rd1、n2R\(_{d2}\)、n\(^{2}\)RL是串联起来的,可用图3等效电路表示,于是可以得出\(\frac{u}{_{1}}\)i1=R\(_{1}\)=n2RL+n\(^{2}\)R\(_{d2}\)+Rd1。令铜损电阻R\(_{c}\)=Rd1+n2R\(_{d2}\),于是可以得出R1= n\(^{2}\)R\(_{L}\)+Rc,或者n2R\(_{L}\)=R1-R\(_{c}\)=R1(1-R\(_{c}\);R1)=R\(_{1}\)·ηc。式中ηc=1-RcR\(_{1}\),它是只考虑铜损情况下变压器的效率。将这个公式改写,可得到
n=\(\frac{\sqrt{ηC·R}}{_{1}}\)RL………………(2)。
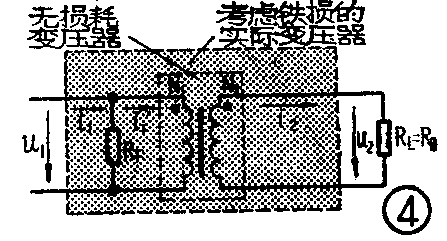
2.铁损。铁损包括变压器的磁滞损失和涡流损失。这部分损耗虽然消耗在铁心里,但归根到底这部分损耗功率要由初级的输入功率供给。图4为单考虑铁损时的等效电路。漏阻RF表示铁损的等效电阻,与初级线圈并联。它的物理意义是:输入电流i\(_{1}\)有一部分要经RF旁路,只有i1′一部分可通过变压器传到次级。也就是说,在输入功率u\(_{i}\)·i1中,只有u\(_{1}\)·i′1一部分送给了负载,即u\(_{1}\)·i′1=u\(_{2}\)·i2。于是i\(_{2}\)/i1′, u\(_{1}\)/u2=n。上两式相乘得n\(^{2}\)=i\(_{2}\)·u1/i\(_{1}\)′·u2,或u\(_{1}\)/i1′=n2R\(_{2}\)=n\(^{2}\)RL。次级负载反射到初级去的阻抗为n2·R\(_{L}\),n\(^{2}\)RL与R\(_{F}\)是并联的,所以初级的等效阻抗
R\(_{1}\)=u1i\(_{1}\)=n\(^{2}\)RL·R\(_{F}\);n2RL+R\(_{F}\)。
也可以改写为
n\(^{2}\)·R\(_{L}\)=R1(n2R\(_{L}\)+RF)R\(_{F}\)=R1;ηF,
式中,ηF=R\(_{F}\)/(n\(^{2}\)RL+ R\(_{F}\)),是只考虑铁损时变压器的效率,这时变压器的变比
n=\(\frac{\sqrt{R}}{_{1}}\)ηF·RL……(3)
以上分别讨论了铜损和铁损两种情况,在计算输出变压器的变比n时,如果变压器较大,则可近似认为以铁损为主,用②式计算;如果变压器较小,则可近似认为以铜损为主,用①式计算。
钢损和铁损都不能忽略怎么办?
在许多情况下,铜损和铁损都不能忽略,大型变压器和小型变压器也没有什么原则的划分界限。这时怎么办呢?
通过前面的分析我们可以看出,所谓铜损,可认为是输入电压在铜损电阻R\(_{c}\)上产生压降所造成的功率损失;即u1/u\(_{2}\)=n/ηC;对于铁损来说,可认为是输入电流被铁损电阻RF旁路分掉了一部分而引起的功率损失,这时i2/i\(_{1}\)=ηF·n。将上两式相乘,则可以得到u1u\(_{2}\)·n\(^{2}\)·ηF;ηc。因为u1/i\(_{1}\)=R1,u\(_{2}\)/i2=R\(_{2}\)=RL,所以这时计算变压比的公式将变为
n=\(\frac{\sqrt{ηC·R}}{_{1}}\)ηF·RL。令C=ηC/ηF,
则上式可写成 n=\(\sqrt{C·}\)\(\frac{R}{_{1}}\)RL………………………(3)
可以看出,当ηC=ηF时,C=1;当ηC>ηF时,C>1;当ηC<ηF时,C<1。利用③式来计算变比n,就准确多了。
怎样事先求出C值呢?我们知道,在设计变压器时,总是事先凭经验估计出变压器的总效率ηB,此时ηB=ηC·ηF。铜损效率ηC也可以凭经验估计,一般说来,ηC≈0.85。ηB、ηC均已知,ηF就可以求出来,于是C=ηC/ηF就可以进行计算了。
例1:已知型号为E146V的收音机输出变压器的总效率ηB≈0.76,初次级阻抗比R\(_{1}\)/RL=300/8,求变压器的变比n。
n=\(\sqrt{C·}\)\(\frac{R}{_{1}}\)RL=ηC\(^{2}\)·R\(_{1}\);ηB·RL=\(\sqrt{.}\)852×3000.76×8≈6。
实际变压器的变比为n=6.15,两者是很近似的。
根据n=\(\frac{ηC}{^{2}}\)·R\(_{1}\)ηB·RL,
可以推导出另一个计算n值的简便公式,这就是
n≈\(\frac{1}{1·1R}\)\(_{L}\)(\(\sqrt{R}\)1·R\(_{L}\);ηB-Rd1R\(_{1}\);RL)。
在设计变压器时,通常是先计算出变压器的初级数据,即由低频响应→初级电感量L1→初级圈数N\(_{1}\)→初级线径d1→初级直流电阻R\(_{d1}\),这时n值就可以进行计算了。
例2:已知R\(_{1}\)/RL=600/8,ηB≈0.72,R\(_{d1}\)≈36欧,初级圈数N1=570圈,求变比n和次级线圈圈数N\(_{2}\)。