二极管正向电阻之谜

我们常常用万用表来测量二极管的正反向电阻，以鉴别其质量的好坏。测量的次数多了，就会发现一种奇怪的现象；用不同型号的表，或同一表而用不同的倍率来测量同一个二极管的正向电阻，测得的数值极不一致，有时大小竟会相差数百倍。表一列出了用MF40型和30型两种表实测一个2CP10型二极管样品的结果——

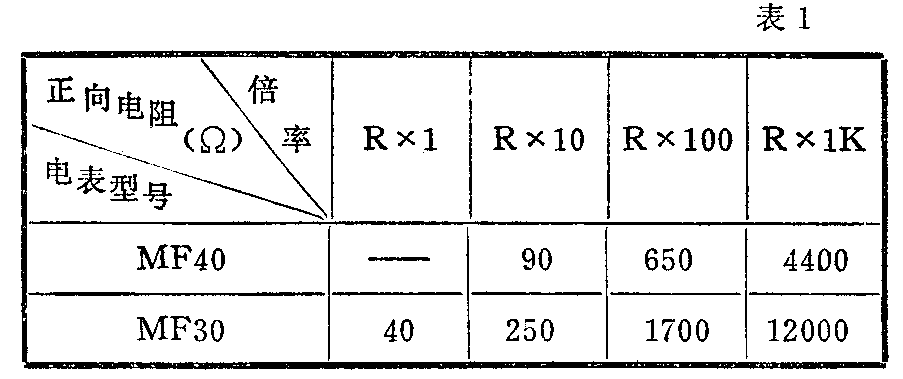
这种现象仿佛是一个费解的谜。究竟是什么原因使测得的结果相差如此之大？测得的这许多数值中，哪一个算是正确的？下文将一步步地揭示这个谜的谜底。

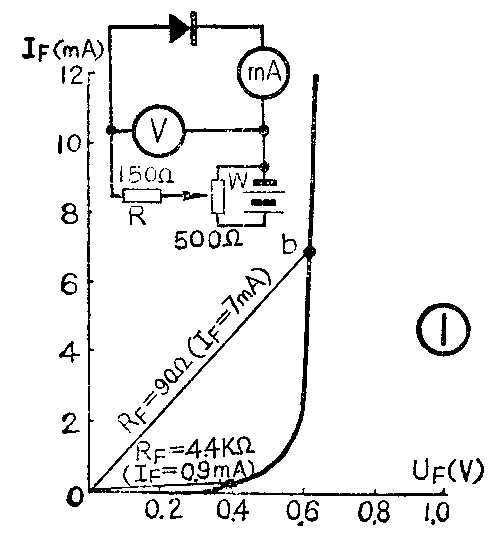
图一所示的二极管正向伏安特性曲线，是根据实测前述样品绘制出来的。一望可知，图象不是一条通过原点的直线，这就可以断定加于二极管的正向电压U\(_{F}\)，与通过二极管的正向电流IF不成正比关系。我们用万用表测得的正向电阻R\(_{F}\)，就是正向电压与正向电流的比值；

U\(_{F}\)与IF既不成正比，则可知R\(_{F}\)决不是一个常量。我们在特性曲线上任意取几个点，来说明这个问题：

当U\(_{F}\)低于0.35V时，二极管处于截止状态，IF=0，则R\(_{F}\)为无穷大。取特性曲线上一点a，这点在横轴上射影为0.4V，在纵轴上射影为0.09mA（图中误写成0.9mA）根据式（1），可算出RF为4.4KΩ，即用40型表R×1K档测得的数值。

再取特性曲线上一点b，这一点在横轴上的射影为0.63V，纵轴上的射影为7mA，同样可以计算出R\(_{F}\)为90Ω，即用40型表R×10档测得的数值。

在观察图象和计算R\(_{F}\)的过程中，不难看出一个关键性的问题：通过二极管的正向电流越大，则它的正向电阻越小；通过二极管的正向电流越小，则它的正向电阻越大。但不存在反比关系。正是由于测试时通过二极管的电流大小不同，因此测得的正向电阻也就大小悬殊了。

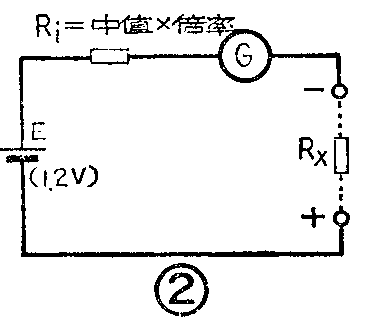
不论用哪一种表、取哪一档倍率，其测量电阻时的电路，均可概括如图②。电源E，多数用一节干电池，其端电压以1.2V为标准进行设计。R\(_{i}\)表示电表里的内阻。RX为被测电阻。G为电流表，用以指示测量回路内的电流I，从而可以在Ω栏刻度内直接读出R\(_{X}\)的数值。G所指示的电流为：

在两表棒短接时，R\(_{X}\)=0，表针指满刻度（即0Ω处）。这时G的满刻度电流Im应该是：

习惯上我们把R×1档的R\(_{i}\)特称做“中值”。40型表的中值为8Ω，30型表的中值比较大，为24Ω。根据式（3），可以计算出来，40型表R×1档的Im为150mA，30型表却只有50mA。

同一表内，各档的R\(_{i}\)是按倍率增大的，而满刻度电流Im，却是按倍率的倒数减小的。以40型表为例，各档的R\(_{i}\)和Im见表2。

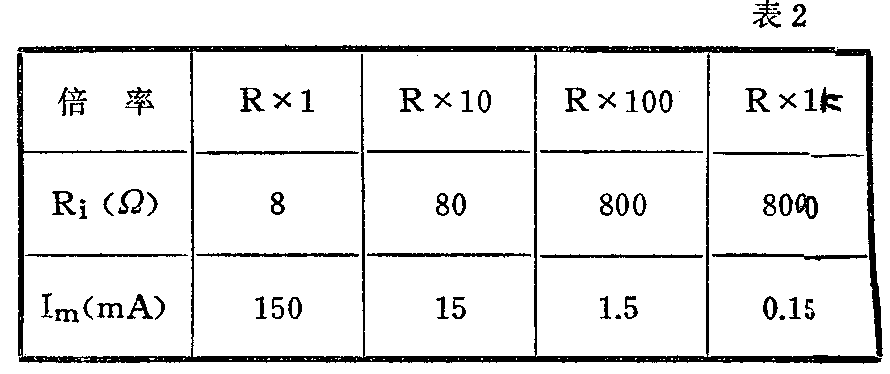
由此可知，在用万用表测量电阻时，表的中值越小，选的倍率越低，R\(_{i}\)越小，测量回路里总的电阻（Ri＋R\(_{x}\)）也就越小，因此通过回路的电流就较大；反之，表的中值越大，选的倍率越高，则通过回路的电流却较小。

现在，谜底终于揭开了：原来，二极管的R\(_{F}\)是因IF的大小而异的。用不同中值的表，或同一表在选用不同倍率的档级测量时，由于表的内阻不一样，那么通过二极管的电流也就大小不同，则测得的正向电阻也就大小不同了。如所用的表中值较小，选用的倍率较低，则通过二极管的电流就比较大，所以测得的正向电阻就比较小；反之，如所用的表的中值较大，选用的倍率较高，则通过二极管的电流就比较小，所以测得的正向电阻就比较大了。我们所测得的许多不同的正向电阻，在一定的条件下都是正确的。但条件变了，它的正确性也不复存在了。用测量正反向电阻以鉴别二极管好坏的方法，因为简便易行，且有一定参考价值，因此大家还是乐于采用的。但是在介绍经验时，一定要说明用怎样的表、选哪一档倍率测量的才有实用意义。例如，用MF40型表的R×100档，测量2AP9等锗管，正向电阻在200Ω左右，反向电阻在200KΩ以上；测量2CP10等硅管，正向电阻在4KΩ左右，反向电阻在1MΩ以上。这样的管子已可以应用的了。（朱蔼初）