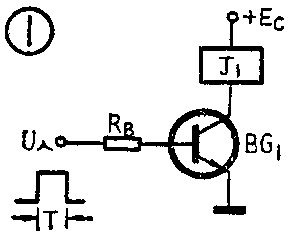
一个带继电器的开关电路(图1),当输入端加上正的矩形脉冲时,晶体管BG\(_{1}\)导通,集电极电流流过继电器线圈J1使继电器吸合。但如果矩形脉冲的宽度很窄,窄到一定程度时继电器却不能吸合,这是什么原因呢?
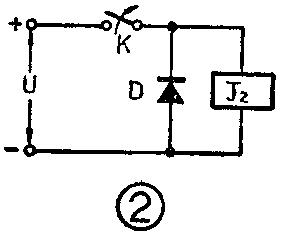
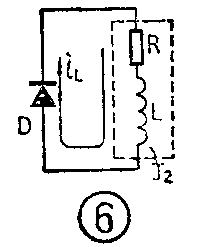
在自动电话交换机和自动控制设备中常常要求继电器在断电后要经过一段时间才使接点释放,即所谓缓放。图2中在继电器线圈两端并联了一个二极管D就达到了缓放的目的,这又是为什么呢?
电流不能突变
要想把一辆静止的汽车开动起来,只能是从慢到快逐渐地加速,它不可能一下子就达到很高的速度。同样,要想让一辆疾驰的车辆立即停住也是不可能的,一定要滑行一段距离。通常我们把这种现象称为惯性。如果用能量的观点来解释,原来能量为零的物体接收能量时,只能从少到多逐渐地接受和积累;而原来有能量的物体放出能量时,也只能从多到少逐渐地输出和释放。这种能量输入输出的过程在时间上可能有长有短,但决不能做到不需要时间,这叫做能量不能突变。
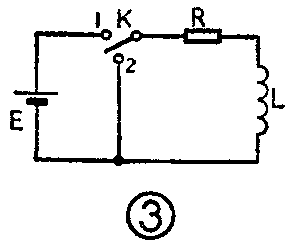
电子电路中能量的传递和转换也是按能量不能突变的规律进行的。例如把图3中开关K突然扳到“1”的位置,电源E就要通过电阻R向电感充电。假如电感上原来没有能量,那么由于惯性作用,电源对它的充电只能从零开始逐渐增加,一直增加到最大值时充电才停止。也就是说对电感的充电,同样是要经过一定的时间的。充电完毕后电源的能量以磁场的形式储存在电感线圈中,它的数值是和流过它的电流IL和电感量L有关的。磁场的能量为:
W\(_{L}\)=\(\frac{1}{2}\)LI\(^{2}\)(1)
当电感中已经储有能量,把开关K从“1”突然扳到“2”时,电感中的能量要通过电阻R和短路线泄放,这个泄放过程同样是需要一定时间的。开关刚从“1 ”扳到“2”的瞬间,电感中的能量处于要泄放而还没有开始泄放的时刻,它的能量仍然保持着原来的数值,因此在这一瞬间流过电感的电流仍要保持原来的大小和方向,好象一辆疾驰的汽车在刹车时由于惯性而仍然要以原来的速度向前冲刺那样。当磁场的能量开始泄放后,电流数值逐渐下降,能量通过电阻R变成热量被消耗掉,到能量全部泄放完,电流也就下降到零。这和一辆汽车在刹车时通过刹车机构以及轮胎和道路的摩擦把能量变成热量消耗掉,经过一段滑行后终于停下来的现象很相似。
可见不论是电感充电时电流从零上升到最大值的过程或是电感放电时电流从最大值下降到零的过程,它们都需要时间而不能突变。这也就是通常所说的电感中电流不能突变。由于电感对电流有着这种惯性似的特性,所以我们把电感称为电流惯性元件。
由于同样的原因,电容器C上的电压也是不能突变的。因为电容器中储存的是电场能,它的大小是和电压高低有关的,所以把电容器称为电压惯性元件。
相同的变化规律
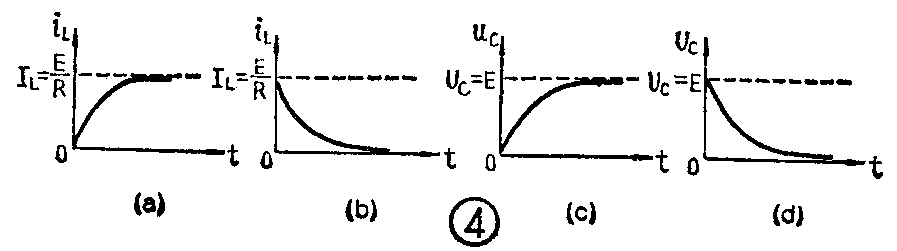
由于电感中电流不能突变,所以电感的充电曲线有着图4a的形状,曲线从零开始的一段很陡,表示电流增长得很快;以后电流增长得速度就逐渐慢下来,曲线越来越平坦;最后电流值趋于稳定,不再增长,稳定电流值为
I\(_{L}\)=E/R (2)
放电电流的曲线则如图4b所示。
把电感的充放电曲线和RC电路的充放电曲线(图4c、d)进行对比,可以看到它们的形状是相似的。也就是说它们有相同的变化规律,都是按数学上“指数曲线”的规律变化的。不同的是:电容器中能量大小是和电压高低有关的,所以曲线的标尺是以电压数值标注的;而电感的充放电曲线则使用电流的数值作标注。
在RC串联电路中,为了研究电路的动作与时间的关系,我们曾使用RC电路的时间常数τC这样一把特殊的“尺子”,配合一条通用的充放电曲线就能使RC电路的分析和计算过程大大简化。那么RL电路中是不是也能找到时间常数这把“尺子”呢?RL电路中的时间常数和它的电路参数之间又将是什么样的关系呢?
从对比中寻找答案
RC电路中,电容器容量C越大,储存的能量也越多,充放电的时间也越长。而在RL电路中,电感L越大,从(1)式看到,电感充电结束时所储存的能量也越多,因此不管是从零充到最大值或从最大值泄放到零,需要的充放电时间也一定越长。
RC电路中,电容器上电压越高,储存的能量越多。而电容器上的电压是靠电流的充电得到的,因此电路中的电阻R直接影响充放电的时间,R的数值越大,充电电流越小,充电需要的时间就越大。因此RC串联电路的时间常数等于R和C的乘积,即τC=RC。
在RL电路中,电感储存的能量是和充电结束后的电流有关的,从(1)式看到,I\(_{L}\)越大,储存的能量越大。但这个电流的数值又是受电路中电阻R控制的:R的数值大,电流IL就小,储存的能量就少,因此充放电需要的时间就短;R的数值小,电流I\(_{L}\)就大,储存的能量就多,充放电需要的时间就长。也就是说,RL电路中时间常数与R的关系和RC电路中时间常数与R的关系正好相反。所以RL电路的时间常数是:
τL=\(\frac{L}{R}\)(3)
我们知道电感量的单位是亨,电阻的单位是欧,所以RL电路时间常数的单位应该是:
可见它的单位也是时间的单位“秒”。
例如一个RL串联电路的R=10KΩ,L=10mH,它的时间常数
τL\(_{1}\)=\(\frac{L}{R}\)=10×10\(^{-}\)3;10×103=1微秒
另一个电路的R=10KΩ,L=1H,
τL\(_{2}\)=\(\frac{L}{R}\)=1;10×10\(^{3}\)=100微秒
与RC电路中充放电的规律相同,大约在5个τ时充放电就基本完成,因此第一个RL电路在5τL\(_{1}\)=5微秒时,充放电就基本完成,而第二个电路则需要5τL2=500微秒。
如果想从充放电曲线上求出时间常数时,同样可以仿照RC电路中求τC的方法,从电感充电曲线上找出充电电流等于最大电流I\(_{L}\)的0.63倍时所需要的时间就是时间常数τL(图5a);而在电感放电曲线上,当电流下降到等于最大电流I\(_{L}\)的0.37倍时所需的时间也正是时间常数τL(图5b)。
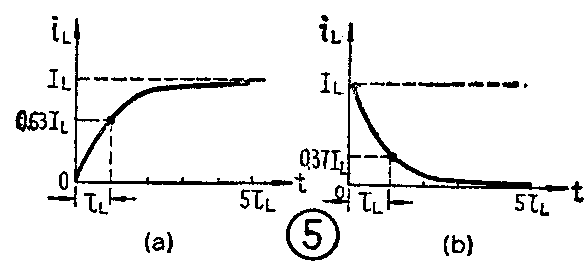
掌握了求时间常数τL的方法后,遇到需要计算RL电路的动作和时间关系等问题时,就可以用时间常数这把“尺子”去分析和研究,这将给我们带来极大的方便。
用时间常数来说明
有了时间常数的知识,图1和图2的问题就很容易解释了。图1的继电器线圈可以等效成一个电感L和电阻R的串联电路,它的时间常数τL=\(\frac{L}{R}\)。当输入正矩形脉冲时,BG\(_{1}\)导通,电源向电感L充电。如果脉冲宽度T比τL大得多,电流有足够的上升时间使继电器吸合。如果脉冲宽度T窄到小于时间常数τL,BG1导通后还没等电流上升到继电器的吸合电流时又重新截止,因此继电器就不能吸合。
图2中的继电器线圈同样可以等效成RL串联电路。开关接通时二极管D反向并联在线圈两端,它对电路没有影响。开关断开的瞬间,由于电感中电流不能突变,电感中储存的能量仍以原来的电流方向通过二极管D放电,如图6。电流的数值从最大值IL按放电曲线下降,下降的快慢由线圈的时间常数决定。当电流下降到等于继电器的释放电流时继电器才释放。从断电到继电器释放的这段时间就是它的缓放时间。我们只要改变电路的时间常数τL,就可以改变它的缓放时间。
在RC串联电路中,当时间常数τC小于脉冲周期T时,电路表现出微分电路的特性,即它能把一个矩形脉冲变换成一对窄的尖脉冲。RL电路中同样也有“电感激分电路”,它的电路如图7。
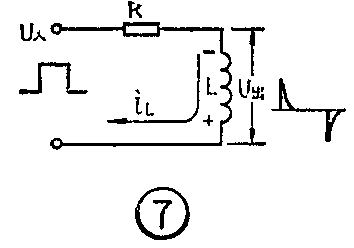
当电路输入端加的是正矩形脉冲,在输入脉冲U\(_{入}\)突然从零上跳到最大值时,相当于RL电路突然和电源接通。由于电感中电流不能突变,在这一瞬间电流仍保持等于零,电阻上电压降UR也等于零,因此电源电压全部加到了电感上。如果电路的时间常数很小,电流会迅速地增加,电阻R上的电压降也就很快地升高,电感上的电压也迅速下降,因此对应于输入正脉冲的上跳部分在输出端得到一个窄的正向尖脉冲。
在输入脉冲从最大值突然下降到零时,相当于RL电路突然被切断电源。由于电感中电流不能突变,仍要保持原来的大小和方向,这个电流只能由电感中储存的磁场能提供,所以在这一瞬间电感线圈相当于一个电源,它的电压大小和电源电压相等,方向则和原来的电流方向一致,也就是极性为上负下正(见图7)。如果电路时间常数很小,电感上的这个电压只能维持极短的时间,于是对应于输入脉冲下跳部分在输出端得到一个负的尖脉冲。
这一对反向的尖脉冲正是我们需要的微分脉冲。而保证这个电路产生微分作用的条件就是时间常数τL必须比输入脉冲宽度T小得多。
由于电感线圈体积大、重量重、制作复杂、因此在脉冲技术中凡是用RC电路可以解决问题的地方一般都尽量避免使用RL电路。只有在特殊情况下,例如需要的触发脉冲很窄,只有几微秒时,常常使用上述“电感微分电路”。实际使用的电路因为要考虑分布电容等因素,所以比图7要复杂一些。有一种称为“峰化电路”的RL电路就是改进的窄脉冲形成电路。
另外,电感线圈是电流惯性元件,电视机中磁偏转的显象管是用电流扫描控制电子束偏转的,所以不得不使用电流惯性元件——磁偏转线圈。(方波)