这里介绍一种调整电阻的方法,既可省去是位器,又可减少调试时更换电阻的麻烦。
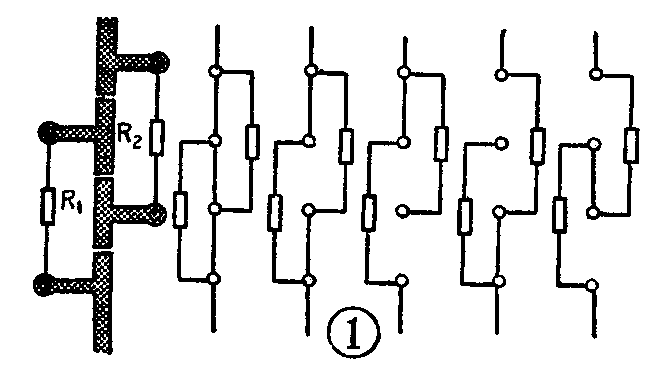
找两个电阻,按照图1所示排列在印刷板上。两个电阻虽只有三个焊接缺口,但却有五种连接的方法,其阻值分别为零;\(\frac{R}{_{1}}\)×R2R\(_{1}\)+R2;R\(_{1}\),R2,R\(_{1}\)+R2。若使它们的阻值比为下列关系:R\(_{1}\):R2=1:2,则分别可得到R\(_{1}\)的0.66、1、2、3的倍数。例如在电路中需要0~15欧姆范围的调整电阻时,R1、R\(_{2}\)可分别为5.1Ω和10Ω,这时可得到0、3.3Ω、5.1Ω、10Ω和15.1Ω。
当电路要求较高时,可以用三个电阻按照图2的方法排列在印刷板上,若使R\(_{1}\):R2:R\(_{3}\)= 1:2:4,有趣的是可以得到17种阻值。当分别将电阻串入(或串联)在电路中时,即可得到R1的八个整数倍:0,1,2,3,4,5,6和7。当在相邻焊点允许连焊的情况下,将电阻并联或串并联时,还可得到下列九种非整数倍的阻值:0.57、O.66、0.8、0.86、1.33、1.71、2.33、2.8和4.66。
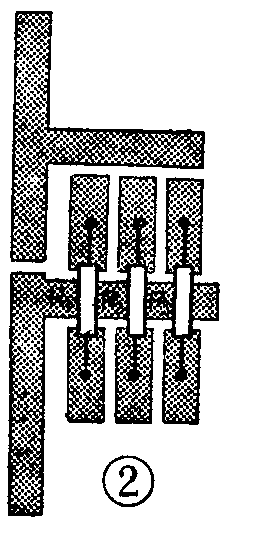
例如在电路中需要0~3.5KΩ调整范围的电阻时,R\(_{1}\)、R2、R\(_{3}\)可分别选用510Ω,1KΩ和2KΩ。显然在整数倍时可得到0,510Ω,1KΩ,1.51KΩ、2KΩ、2.51KΩ、3KΩ和3.51KΩ八种阻值。在分数倍数时约可得到290Ω,340Ω,410Ω,440Ω,680Ω,870Ω,1.19KΩ,1.43KΩ和2.38KΩ共九种阻值。通常在实际调整时,可用整数倍连接,而不必计算,先连焊中心整倍数4,将电阻R3串入电路中,然后再根据情况增加或减少。如需要调整范围再细微时,再按分数倍连焊。
图2的排列虽然焊点不多,却有17种不同的连接方法,亲爱的读者,你是否能够画出来?(郑诗卫)