今年第六期本刊曾介绍过RC串联电路的时间常数τ的意义。时间常数τ在电子电路,特别是在脉冲电路中,是一个很重要的参数。例如,利用RC充放电原理作成的延时继电器,其延迟时间是直接和时间常数τ有关的。而在RC正弦波振荡器、多谐振荡器、锯齿波发生器中,时间常数τ则直接决定着它们的振荡频率。在单稳电路中,时间常数又对输出波形的宽度起着决定性的作用。因此在上述电路中,多数情况下都需要求出τ的数值。那么,应当怎样来求呢?
困难在何处
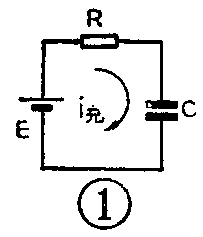
图1是一个简单的RC串联电路,计算这个电路的时间常数是很容易的。只要把电阻和电容的数值相乘就得到时间常数τ=RC。实际的电路并不都是这样的简单电路,往往是由电阻、电容混联而成。对这些复杂的电路可以用等效变换的方法把它变成简单的RC串联电路,然后再求出RC的乘积。
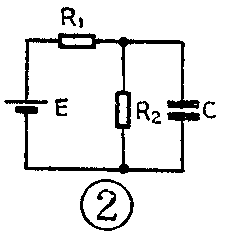
在进行电路的变换和化简时,串并联的计算是比较容易的,遇到的困难主要是电源的问题。例如图2有两个电阻\(_{R}\)1、R2和一个电容C,要计算它的时间常数,总的等效电阻应该是多少呢?
又如图3有两个电容C\(_{1}\)、C2和一个电阻R,这个电路的时间常数又该怎样计算呢?
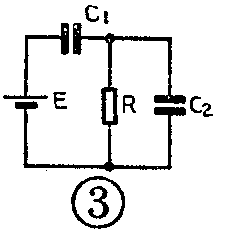
象图2、图3这样的RC电路,由于电源的存在,变换时需要用等效电源变换的原理,这对一般读者来说是较难理解的。能不能绕过这个问题,从时间常数本身的特点出发找到另外一条出路呢?
放电回路的启示
从τ=RC个式子看到,时间常数τ只与R和C的数值有关,与电源是无关的。因此如果能设去掉,就可使问题变得简单起来。
如果在图1的RC电路充电完成后,再把它接成图4那样的电路放电。因为放电时的RC电路和充电时的形式相同,元件参数不变,所以两个电路的时间常数是相等的,即τ=τ\(_{充}\)=τ放=RC。这说明一个RC串联回路并不因为它从充电变到放电而改变它的时间常数。由此可知:计算RC电路的时间常数可以从它的放电电路着手。
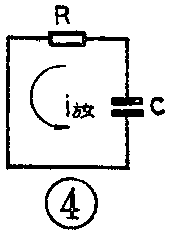
对比图4和图1可以看到,只要把电源短路,RC电路就变成了它的放电形式。这样一来,就可以甩掉电源,经过一般的变换和化简求出它的时间常数了。这种方法不仅对简单的RC串联电路是适用的,就是复杂的RC电路也同样是适用的。因此,在遇到带有电源的RC电路时,只要把电路中的电源短路,再用一般的变换和化简方法把电路简化成一个等效的RC串联电路,最后求出RC的乘积就是它的时间常数。
从复杂到简单
有了这个方法我们就可以计算图2电路的时间常数。首先把图2中的电源短路变成它的放电电路(图5a)。显然,图中的R\(_{1}\)和R2是并联的关系,可以用一个等效电阻R来代替(图5b)。于是这个电路的时间常数就等于:
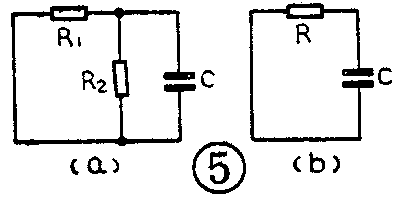
τ =R·C=\(\frac{R1·R2}{R1+R2}\)·C
用同样的方法可以计算图3电路的时间常数。把图3中的电源短路成图6a,它是两个电容C1、C2并联对电阻R放电,因此可以用一个等效电容C来代替这两个电容:C=C\(_{1}\)+C2,电路简化成图6b。因此这个电路的时间常数是:
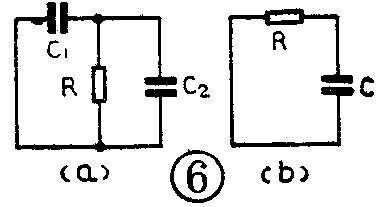
τ=R·C=R(C\(_{1}\)+C2)
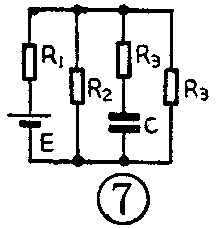
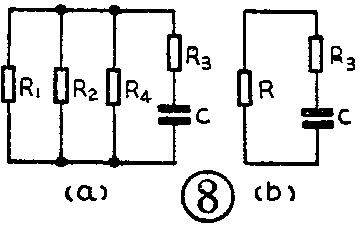
使用这个方法,即使很复杂的RC电路,也能方便地求出它的时间常数。例如图7这样复杂的RC电路,在把电源短路后成为图8a,再简化成图8b。可以看到,这个放电电路的等效电阻是R\(_{1}\)、R2、R\(_{4}\)并联后再和R3串联。所以它的时间常数等于:
通过以上讨论,我们可以把计算RC电路时间常数的方法归纳成以下几点:
(1)如果RC电路中的电源是电压源形式(前面介绍的电路都是电压源形式),先把电源短路而保留其串联内阻。
(2)把去掉电源后的电路简化成一个等效电阻R和等效电容C串联的RC放电回路,等效电阻R和等效电容C的乘积就是电路的时间常数。
(3)如果电路使用的是电流源的形式(图9),那么首先应该把电流源开路而保留它的并联内阻(图10),再按简化电路的方法求出时间常数。
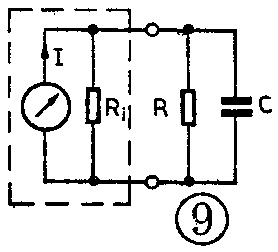
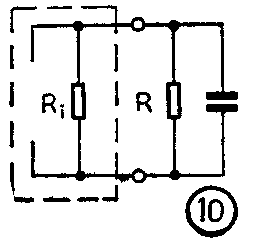
(4)计算电路的时间常数时要注意各个参数的单位。当电阻的单位是“欧”,电容的单位是“法”时,乘得的时间常数的单位才是“秒”。
利用曲线求时间常数
RC电路的充放电曲线,不仅可以用来表示充放电规律,还可以利用它直接求出时间常数。
我们知道,RC电路在充电时,当电容器上充电的电压等于电源电压的0.63倍时,所用去的充电时间恰好等于时间常数τ。RC电路在放电时,当电容器上的电压下降到等于电源电压的0.37倍时,所用去的放电时间也正好等于时间常数τ。利用这个关系就可以从充电或放电曲线上迅速找到时间常数τ的具体数值(图11)。
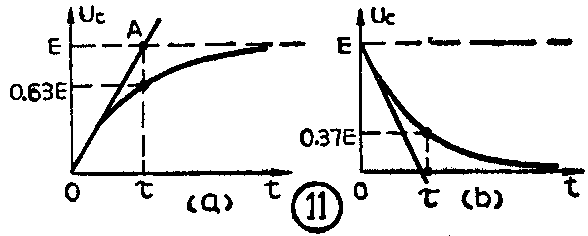
在很高频率下工作的RC电路,寄生电容的影响往往很大。这时如果只以电路中元件的标称值作计算的依据往往很难得到正确的结果。如果能用实验的方法作出充放电曲线,再从曲线上按上述方法求出电路的时间常数,就能得到较为切合实际的结果。
用充放电曲线求时间常数还有另一种方法:如果是充电曲线,可以通过充电曲线的起始点作充电曲线的切线,它与充电终了值E所对应的那条水平线交于A点,该点所对应的时间就是电路的时间常数τ的值(图11a)。如果是放电曲线,可以通过放电曲线的起点作放电曲线的切线,它与座标横轴相交的那一点所对应的时间也正是时间常数τ的值(图11b)。(方波)